Hans Walser, [20170320]
Prozentuale VerŠnderungen
Anregung: A. B., F.
1 Worum geht es?
Ausgehend von einer Prozent-Aufgabe werden Probleme mit prozentualen VerŠnderungen besprochen.
2 Die Aufgabe
Die Aufgabe entstammt dem COSH-Mindestanforderungskatalog [COSH] fŸr MINT- StudiengŠnge (Aufgabe 34):
Wie verŠndert sich der FlŠcheninhalt eines rechtwinkligen Dreiecks, wenn eine der Katheten um 20 % verkŸrzt und die andere um 20 % verlŠngert wird?
3 Besprechung der Aufgabe
3.1 Kompensation?
ãVerkŸrzenÒ und ãverlŠngernÒ kompensieren sich nicht. Dies wird sofort klar, wenn wir die Aufgabe dynamisch denken und mit 100% arbeiten. Dann wird die FlŠche null.
3.2 Grafische Lšsung
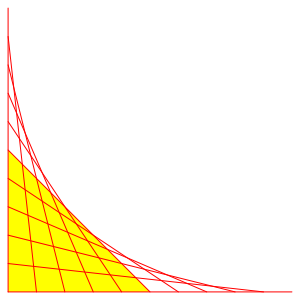
Abb. 2: Grafische Lšsung
In der Abbildung 1 starten wir mit einem rechtwinklig gleichschenkligen Dreieck (gelb). Die Katheten werden um 20%, 40%, 60%, 80%, 100% verlŠngert und verkleinert. Man ãsiehtÒ, wie die Dreiecke flŠchenmŠ§ig kleiner werden. In den GrenzfŠllen ist der FlŠcheninhalt null.
Die Enveloppe der Hypotenusen hat die Gleichung (KathetenlŠnge des gelben Dreiecks gleich ½):
(1)
Sie liegt auf einer (schrŠgen) Parabel, deren Achse die Symmetrieachse der Gesamtfigur ist.
3.3 SchulmŠ§ige Lšsung
Wir arbeiten mit Faktoren. VerkŸrzen um 20% bedeutet einen Faktor 0.8, verlŠngern um 20% einen Faktor 1.2. Nun ist 0.8 × 1.2 = 0.96. Der FlŠcheninhalt wird also um 4% kleiner.
Allgemein:
(1)
In
anderer Darstellung mit 
:
(2)
Der FlŠcheninhalt wird also auf jeden Fall kleiner.
3.4 Allgemeines Dreieck
Die Aufgabe ãhŠngtÒ nicht am rechtwinkligen Dreieck. Wir kšnnen, ohne am Resultat etwas zu Šndern, verallgemeinern wie folgt:
Wie verŠndert sich der FlŠcheninhalt eines Dreiecks, wenn eine Seite um 20 % verkŸrzt und eine andere Seite um 20 % verlŠngert wird?
Es gibt verschiedene Mšglichkeiten, dies einzusehen.
Statt mit einem Dreieck kšnnen wir auch mit einem Rechteck oder einem Parallelogramm arbeiten.
4 Im Raum
4.1 Aufgabe
Wie verŠndert sich das Volumen eines Zylinders, wenn seine Hšhe um 20% verkŸrzt und sein Radius um 20% verlŠngert wird?
Nun ist 0.8 × 1.22 = 1.152. Das Volumen wird um 15.2% vergrš§ert. Andererseits: bei 100% erhalten wir eine flache Scheibe mit dem Volumen null.
Sehen wir das genauer an:
|
Prozentsatz |
0% |
20% |
40% |
60% |
80% |
100% |
|
VerŠnderung |
0% |
15.2% |
17.6% |
2.4% |
–35.2% |
–100% |
Tab. 1: VerŠnderungen
In der Gegend von 40% haben wir offenbar die maximal mšgliche Vergrš§erung des Volumens. Etwas oberhalb von 60% haben wir keine VerŠnderung. Daher neue Aufgabe:
4.2 Neue Aufgabe
Wir verkŸrzen die Hšhe eines Zylinders um p% und verlŠngern den Radius um p%.
a) FŸr welchen Wert von p wird das Volumen maximal?
b) FŸr welchen Wert von p ergibt sich keine VolumenŠnderung?
Mit der
Schreibweise 
haben wir folgende Funktion zu
diskutieren:
(3)
Die Abbildung 2 zeigt den Funktionsgrafen.
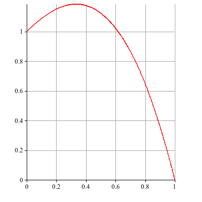
Abb. 2: Funktionsgraf
4.3 Kurvendiskussion
Teilaufgabe a): Es ist:
(4)
FŸr die Ableitung erhalten wir:
(5)
Die
Ableitung hat die Nullstellen 
. Das maximale Volumen erhalten wir fŸr 
.
Teilaufgabe b): Gesucht sind die Lšsungen von:
(6)
Wir erhalten die kubische Gleichung:
(7)
Umgeformt:
(8)
Die
Lšsungen sind 
. Die Lšsung null ist trivial, wer nichts tut, macht
nichts Falsches. Die positive Lšsung im zulŠssigen Bereich ist:
(9)
Dies ist der Goldene Schnitt (Walser 2013).
Die Abbildung 3 zeigt einen beliebigen Originalzylinder (links) und einen verŠnderten, aber volumengleichen Zylinder.
Abb. 3: Volumengleiche Zylinder
Literatur
Walser, Hans (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wu§ing Ÿber populŠrwissenschaftliche Mathematikliteratur aus Leipzig. Edition am Gutenbergplatz, Leipzig. ISBN 978-3-937219-85-1.
Websites
[COSH] COSH – Cooperation Schule - Hochschule (20.3.2017)
https://lehrerfortbildung-bw.de/bs/bsa/bk/bk_mathe/cosh_neu/
https://lehrerfortbildung-bw.de/u_matnatech/mathematik/bs/bk/cosh/katalog/makv2.pdf