Hans Walser, [20220415]

Punktraster

Idee und Anregung: Lutz-Westphal (2022).

1 Worum geht es?

Kinematisches Spiel im Quadratraster und im Dreiecksraster.

2 Punktraster

Die Abbildung 1 zeigt zwei kongruente quadratische Punktraster. Die Punkte sind mit einer Transparenz von 50% gezeichnet. Bei einer Überlagerung erscheinen sie lila.

Die Punkte approximieren eine Kreisscheibe. Dies ist rein technisch-ästhetisch bedingt, damit keine Ecken vorstehen.

Abb. 1: Punktraster

3 Überlagern und Verdrehen

Nun überlagern wir die beiden Raster im Mittelpunkt und verdrehen den blauen Raster (Abb. 2).

Abb. 2: Überlagerung

4 Unschöne Standbilder

Die Abbildung 3 zeigt die Situation für eine Verdrehung von 45°.

Abb. 3: Verdrehung um 45°

In der Mitte haben wir nach Konstruktion eine exakte blau-rote-Überlagerung, also lila. Rechts davon, und zwar sieben Einheiten im roten Raster, scheint es wieder eine blau-rote-Überlagertung zu geben. Diese ist aber nicht exakt, denn im blauen Raster haben wir die Länge 5*sqrt(2) ≈ 7.071 > 7. Man sieht auch, dass der blaue Punkt etwas rechts über dem roten liegt. Wegen der Irrationlität von sqrt(2) gibt es nirgends mehr eine exakte blau-rote-Überlagerung. Das Muster hat also keine regelmäßige Translationssymmetrie.

Auch bei einer Verdrehung um 60° gibt es keine regelmäßige Translationssymmetrie (Abb. 4).

Abb. 4: Verdrehung um 60°

5 Schönes Standbild

Bei einer Verdrehung um arctan(4/3) ≈ 53.13° ergeben sich (unendlich) viele exakte blau-rote-Überlagerungen (Abb. 5). Diese lila Punkte bilden ihrerseits ein Quadratraster (Abb. 5).

Abb. 5: Verdrehung um arctan(4/3) ≈ 53.13°

6 Das gute alte Lehrer-Dreieck

Die meisten Pythagoras-Aufgaben arbeiten mit dem rechtwinkligen Dreieck mit dem Seitenverhältnis a:b:c = 3:5:6. So auch hier (Abb. 6).

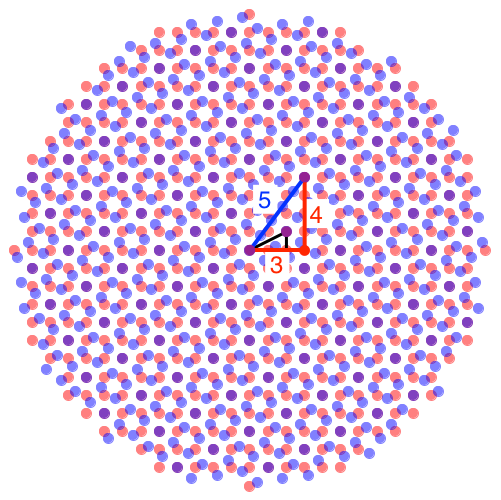
Abb. 6: Das Lehrer-Dreieck

Das Lehrer-Dreieck hat die Katheten der Längen 3 und 4 im roten Raster und die Hypotenuse der Länge 5 im blauen Raster. Der benötigte Drehwinkel ist daher arctan(4/3) ≈ 71.57°. Dies ist der Winkel beta in der üblichen Beschriftung.

Weiter sehen wir ein kleineres rechtwinkliges Dreieck mit den Kathetenlängen 2 und 1 im roten Raster. Daraus ergibt sich für das lila Quadratraster eine Maschenweite sqrt(5). Die Zahlen 2 und 1 sind die sogenannten Parameter des Lehrerdreiecks. Dazu mehr im folgenden Abschnitt.

Die Figur hat Translationssymmetrie.

7 Erinnerung: pythagoreische Dreiecke und Zahlentripel

Zu zwei gegebenen Zahlen (Parametern) m und n mit m > n > 0, gcd(m,n) = 1 und modp(m - n, 2) = 1 (in Worten: m und n sind teilerfremd und nicht beide ungerade) bilden die drei Zahlen:

a = m^2 – n^2, b = 2*m*n, c = m^2 + n^2

ein primitives (teilerfremdes) pythagoreische Zahlentripel. Das rechtwinklige Dreieck mit den Kathetenlängen a und b hat die Hypotenusenlänge c. Es ist ein pythagoreisches Dreieck.

Die Tabelle 1 zeigt die ersten Beispiele. Die Nr.1 ist das Lehrerdreieck

Nr.	m	n	a	b	c	beta [°]
1	2	1	3	4	5	53.13010234
2	3	2	5	12	13	67.38013503
3	4	1	15	8	17	28.07248693
4	4	3	7	24	25	73.73979531
5	5	2	21	20	29	43.60281896
6	5	4	9	40	41	77.31961646
7	6	1	35	12	37	18.92464441
8	6	5	11	60	61	79.61114216
9	7	2	45	28	53	31.89079179
10	7	4	33	56	65	59.48976262
11	7	6	13	84	85	81.20258926
12	8	1	63	16	65	14.25003270
13	8	3	55	48	73	41.11209043
14	8	5	39	80	89	64.01076642
15	8	7	15	112	113	82.37185031
16	9	2	77	36	85	25.05761541
17	9	4	65	72	97	47.92497795
18	9	8	17	144	145	83.26707863
19	10	1	99	20	101	11.42118627
20	10	3	91	60	109	33.39848846
21	10	7	51	140	149	69.98404039
22	10	9	19	180	181	83.97442501

Tab. 1: Pythagoreische Zahlentripel

8 Weitere schöne Beispiele

Zu jedem pythagoreischen Zahlentripel gibt es eine Figur mit Translationssymmetrie (Abb. 7 und 8).

Abb. 7: Nr. 2

Abb. 8: Nr. 5

9 Dreiecksraster

Es geht auch mit einem Dreiecksraster (Abb. 9).

Abb. 9: Dreiecksraster

10 Unschönes Standbild

Die Abbildung 10 zeigt eine Verdrehung um 30°.

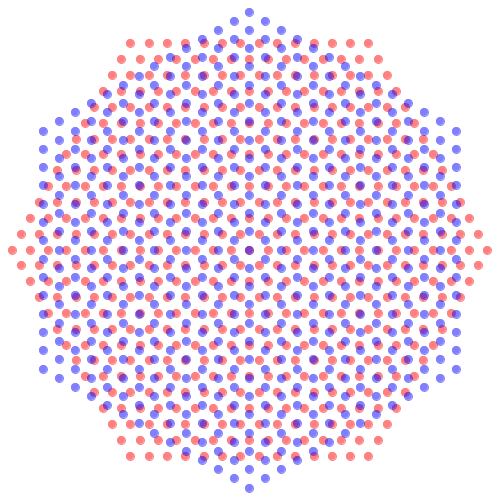
Abb. 10: Verdrehung um 30°

Im Zentrum haben wir eine exakte blau-rote-Überlagerung. Rechts davon, und zwar sieben Einheiten im roten Raster, scheint es wieder eine blau-rote-Überlagertung zu geben. Diese ist aber nicht exakt, denn im blauen Raster haben wir die Länge 4*sqrt(3) ≈ 6.928 < 7. Man sieht auch, dass der blaue Punkt etwas links über dem roten liegt. Wegen der Irrationlität von sqrt(3) gibt es nirgends mehr eine exakte blau-rote-Überlagerung. Das Muster hat also keine regelmäßige Translationssymmetrie.

11 Ein schönes Standbild

Bei einer Verdrehung um arcsin(5/7*sqrt(3)/2) ≈ 38.213° ergeben sich unendlich viele exakte blau-rote-Überlagerungen. Diese bilden ein Dreiecksraster (Abb. 11).

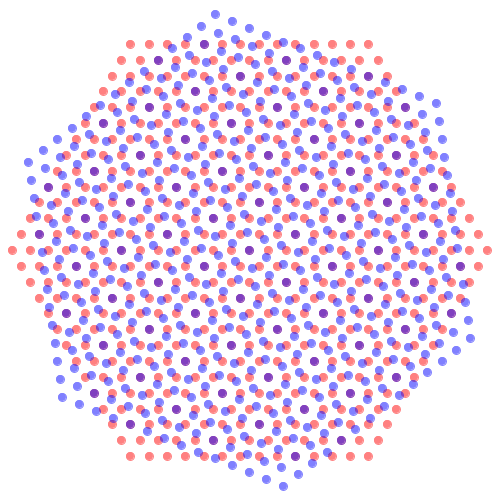
Abb. 11: Exakte Überlagerungen

Hintergrund: Das Dreieck mit dem Seitenverhältnis a:b:c = 3:5:7 hat den Winkel gamma = 120° (Abb. 12). Die Seitenlängen a und b spielen im roten Raster, die Seitenlänge c im blauen. Der Drehwinkel arcsin(5/7*sqrt(3)/2) ≈ 38.213° ergibt sich aus dem Sinus-Satz.

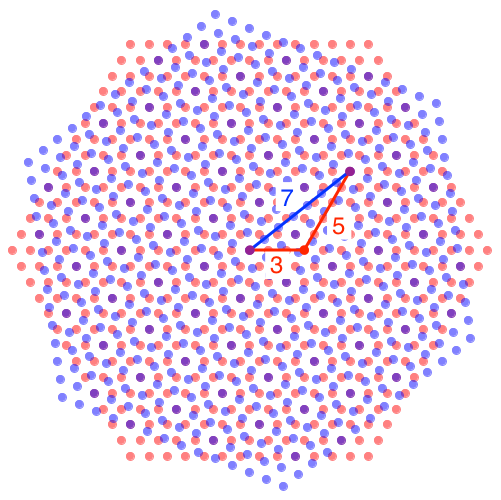
Abb. 12: „Pythagoreisches“ 120°-Dreieck

Dreiecke mit ganzzahligen Seitenlängen und dem Winkel gamma = 120° (oder 60°) sind das Analogon zu den pythagoreischen rechtwinkligen Dreiecken. Es gibt dazu analoge Formeln und Eigenschaften.

Literatur

Hoehn, Alfred und Walser, Hans (2003): Gittergeometrie und pythagoreische Dreiecke. Praxis der Mathematik (5/45), 215-217.

Lutz-Westphal, Brigitte (2022): Gleichmäßig ungleichmäßig. Die Seite für Kinder. Mitteilungen der Deutschen Mathematiker-Vereinigung DMV. 2022. 30. 1. S.80. DOI 10.1515/dmvm-2022-0025.

Walser, Hans (1995): Pythagoreische Dreiecke in der Gittergeometrie. Didaktik der Mathematik, 23, 193-205.

Walser, Hans (1999): Pythagoreische Dreiecke und Gittergeometrie. Beiträge zum Mathematikunterricht 1999. Vorträge auf der 33. Tagung für Didaktik der Mathematik vom 1. bis 5.3.1999 in Bern. Für die GDM herausgegeben von Michael Neubrand. Hildesheim: Franzbecker, 1999. ISBN 3-88120-304-4. S. 575-577

Walser, Hans (2000): Lattice Geometry and Pythagorean Triangles. ZDM Zentralblatt für Didaktik der Mathematik. Jahrgang 32, Heft 2, S. 32 - 35

Weblinks

Hans Walser: Punktraster

http://www.walser-h-m.ch/hans/Miniaturen/P/Punktraster/Punktraster.htm