Hans Walser, [20240620]

Punktsymmetrie

Anregung: Wilfried Dutkowski, Bonn

1 Worum es geht

Punktsymmetrische Schließungsfigur

Poncelet

2 Basis

Einer beliebigen Ellipse beschreiben wir ein Parallelogramm ein (Abb. 1). Ellipse und Parallelogramm haben dasselbe Symmetriezentrum.

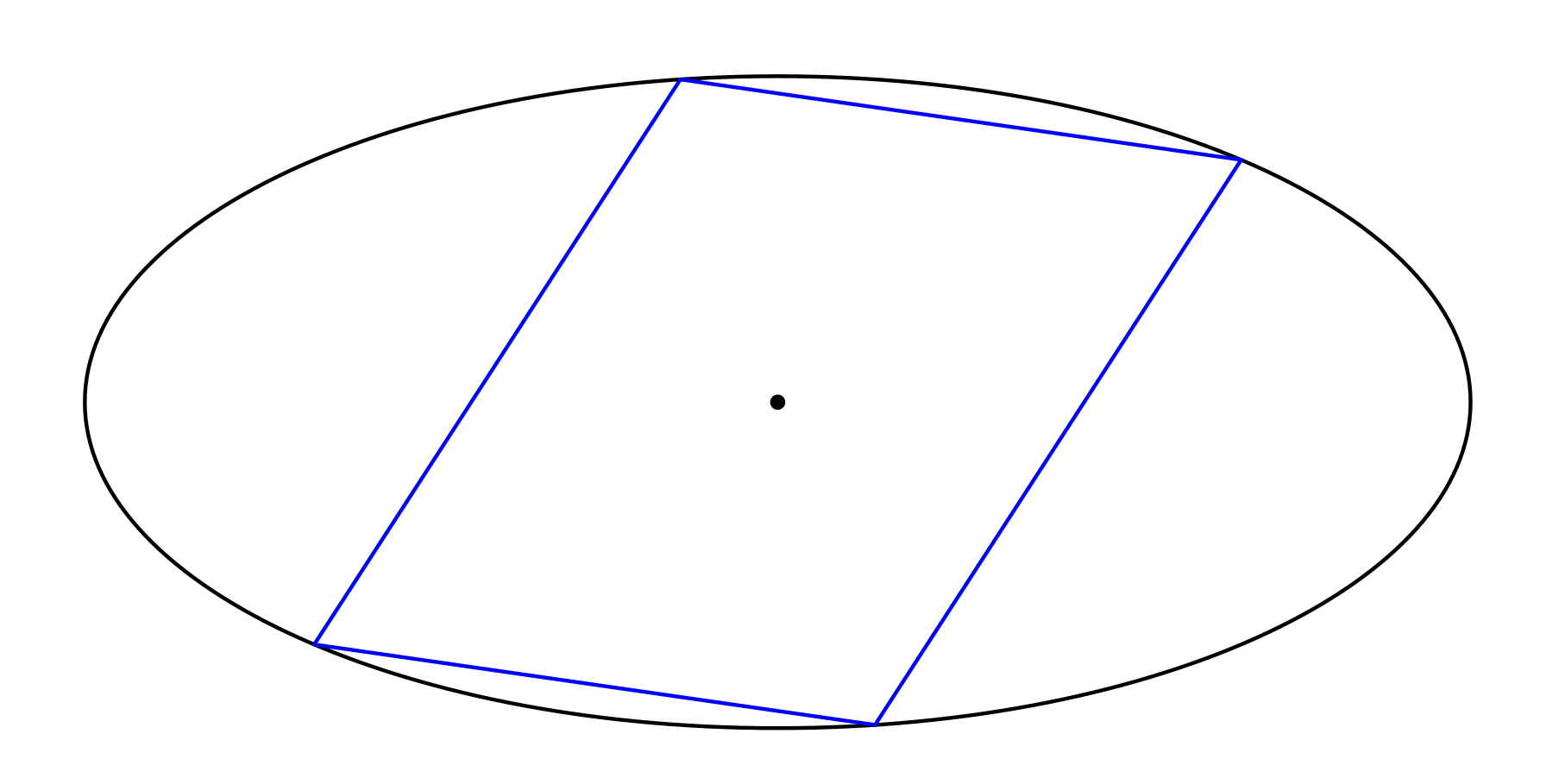
Abb. 1: Ellipse und Parallelogramm

Dem Parallelogramm beschreiben wir eine Ellipse durch die Kantenmitten ein (Abb. 2). Man beachte, dass die beiden Ellipsen nicht achsenparallel sind. Sie haben aber dasselbe Symmetriezentrum.

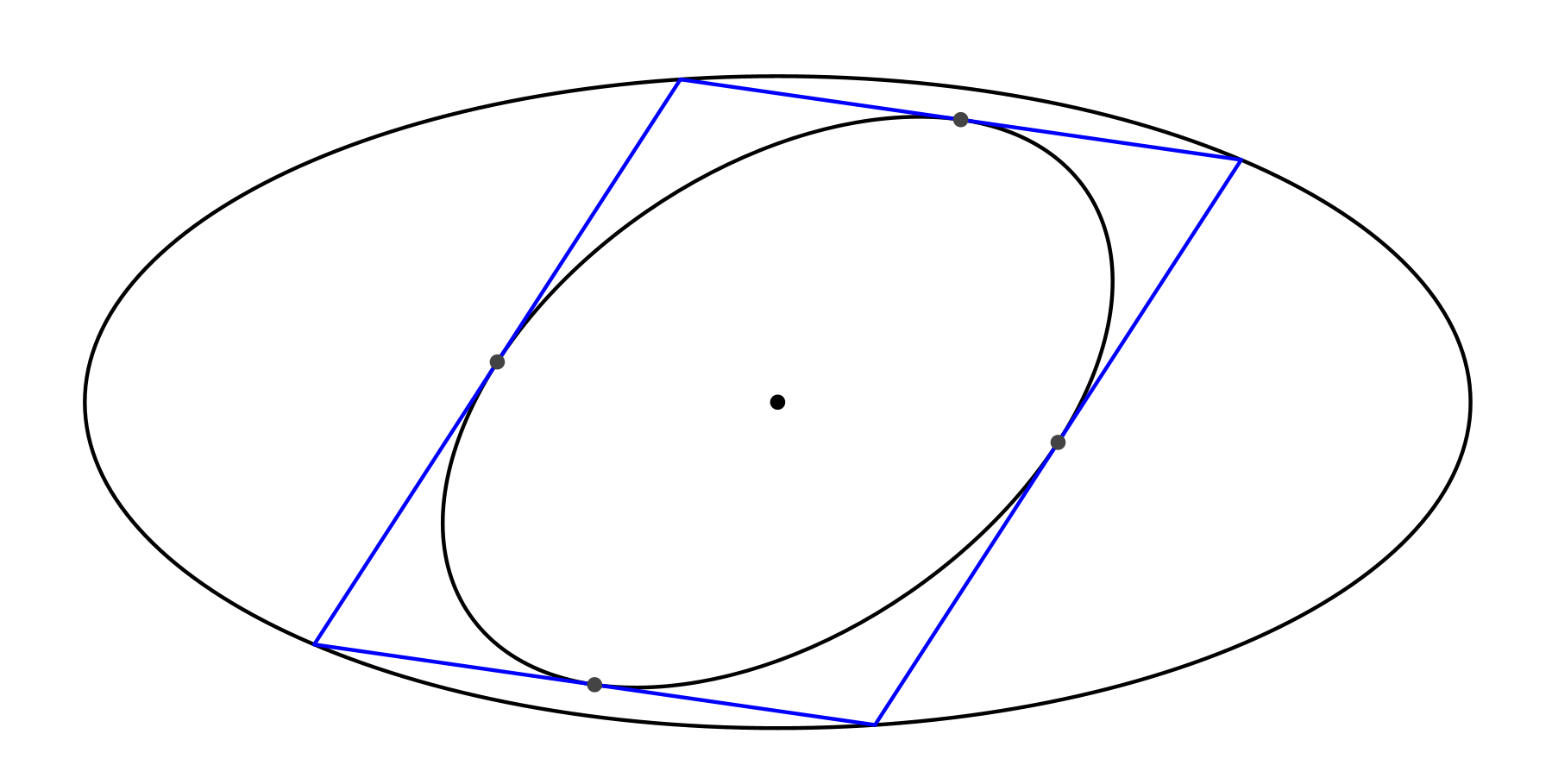
Abb. 2: Noch eine Ellipse

3 Schließungsfigur

Auf der äußeren Ellipse wählen wir einen beliebigen Startpunkt P₀ (Abb. 3).

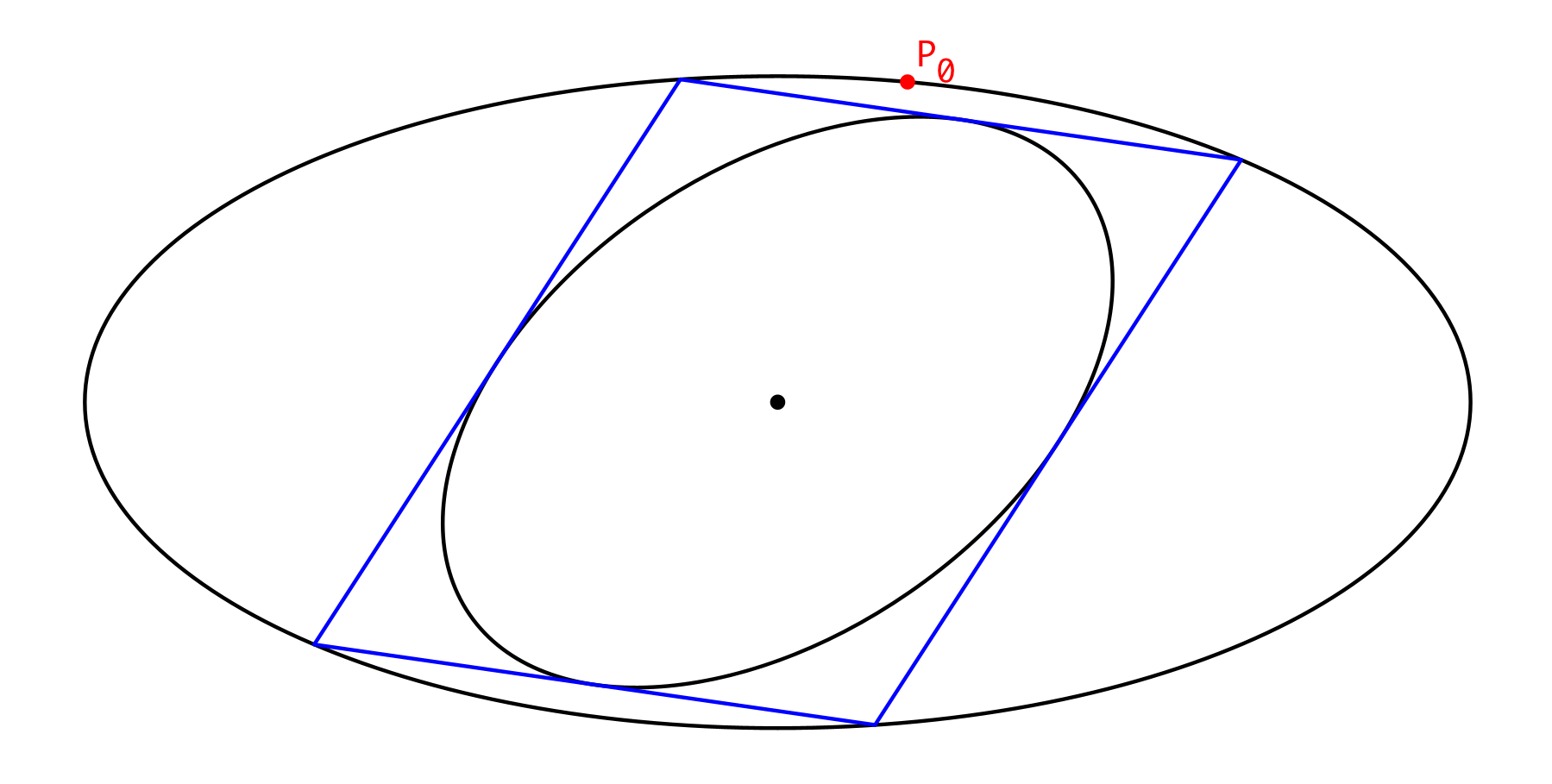
Abb. 3: Startpunkt

Wir zeichnen von P₀ aus eine Tangente an die innere Ellipse, welche von P₀ aus gesehen rechts an der inneren Ellipse vorbeigeht (Abb. 4). Den zweiten Schnittpunkt der Tangente mit der äußeren Ellipse bezeichnen wir mit P₁.

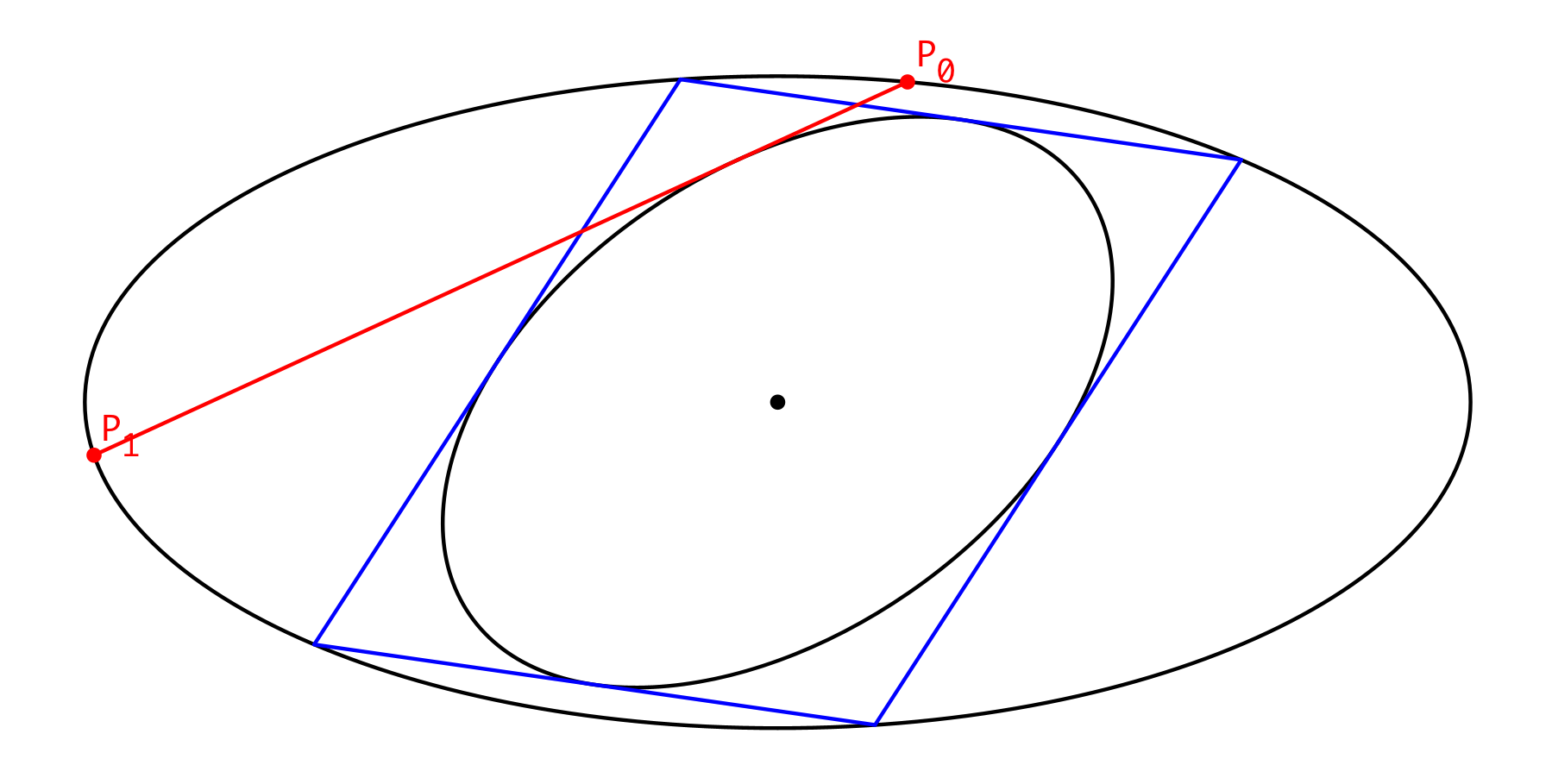
Abb. 4: Erster Schritt

Wir wiederholen das Prozedere, nun von P₁ ausgehend und erhalten P₂ (Abb. 5).

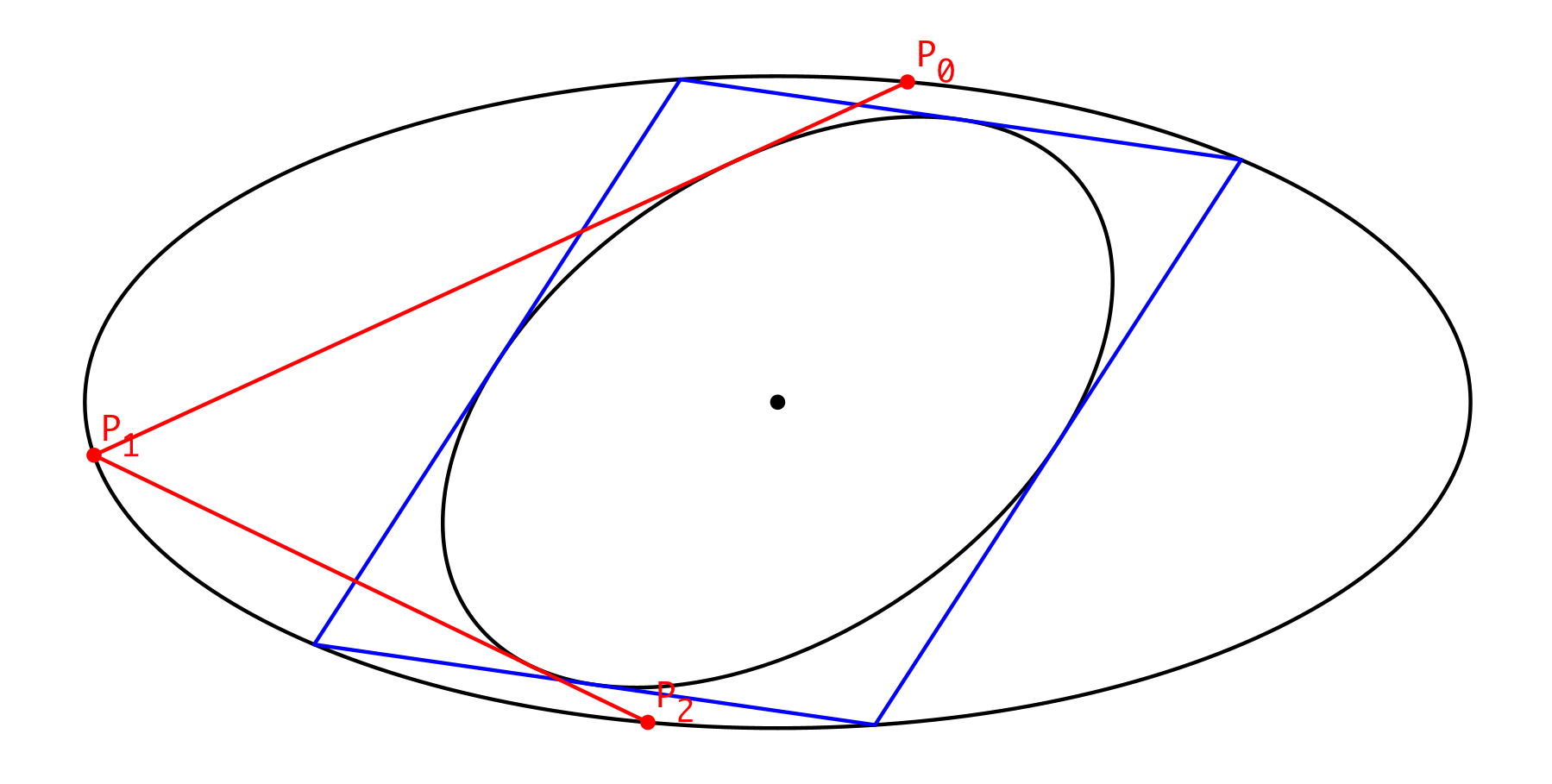
Abb. 5: Zweiter Schritt

Analog der dritte Schritt (Abb. 6).

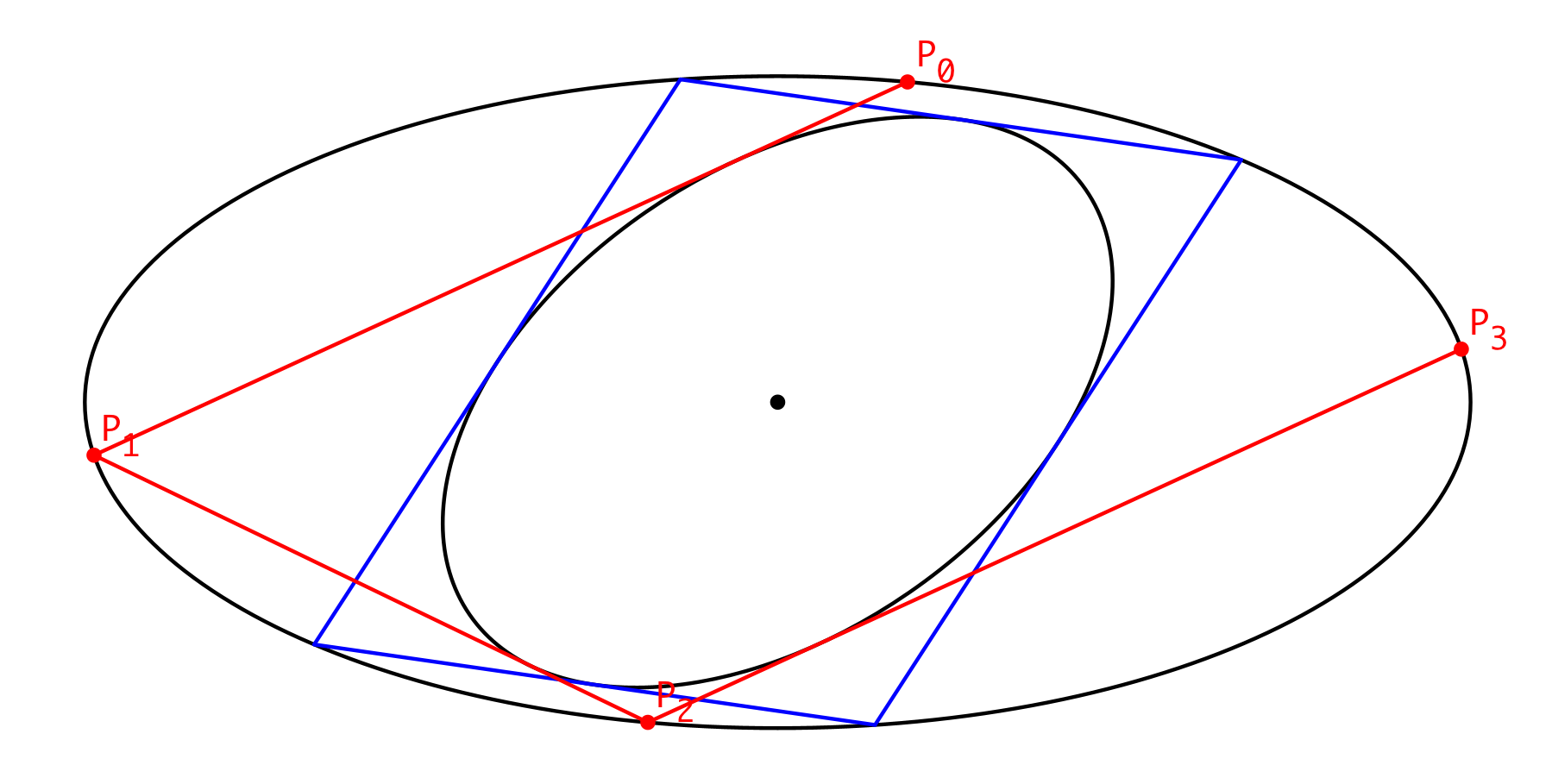
Abb. 6: Dritter Schritt

Der vierte Schritt ist bereits der letzte. Wir kommen zu P₀ zurück (Abb. 7). Die Figur schließt sich.

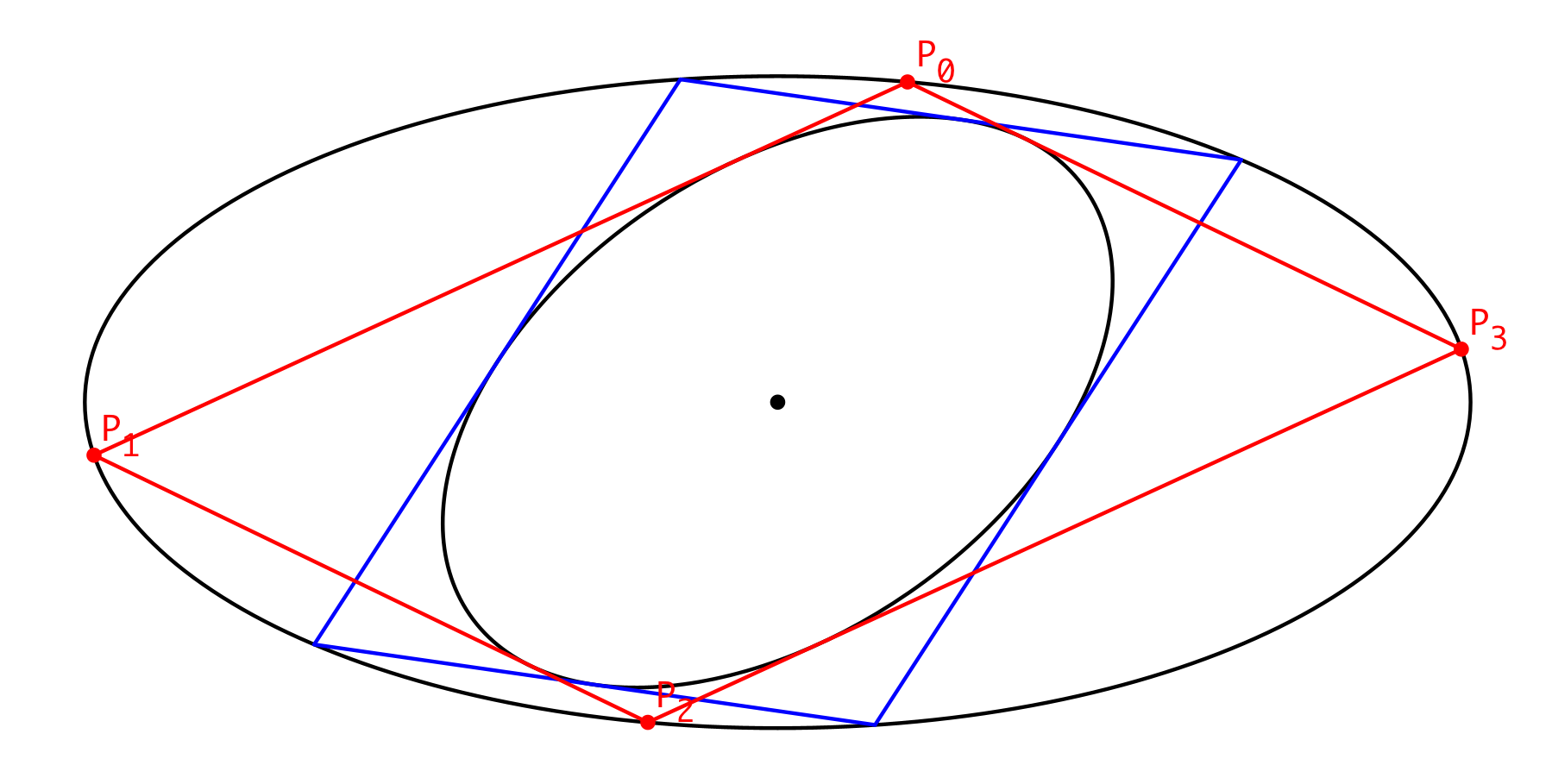
Abb. 7: Letzter Schritt

4 Beweis

Die Schließungseigenschaft ergibt sich aus dem Satz von Poncelet.

Da zudem die Basis punktsymmetrisch ist, gilt dies auch für die Schließungsfigur P₀P₁P₂P₃. Sie ist also ein Parallelogramm.

5 Variation des Startpunktes

Wir können den Startpunkt beliebig wählen (Abb. 8). Alle Schließungsfiguren sind Parallelogramme.

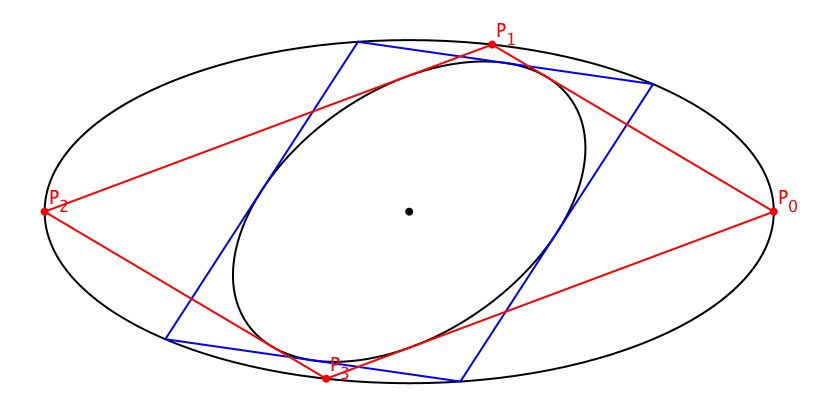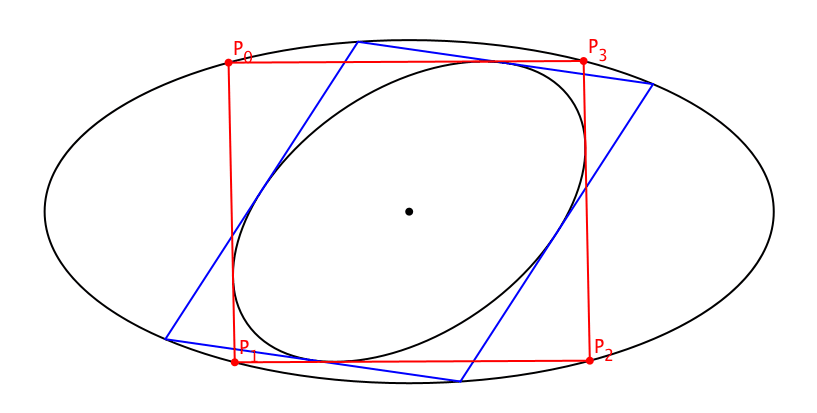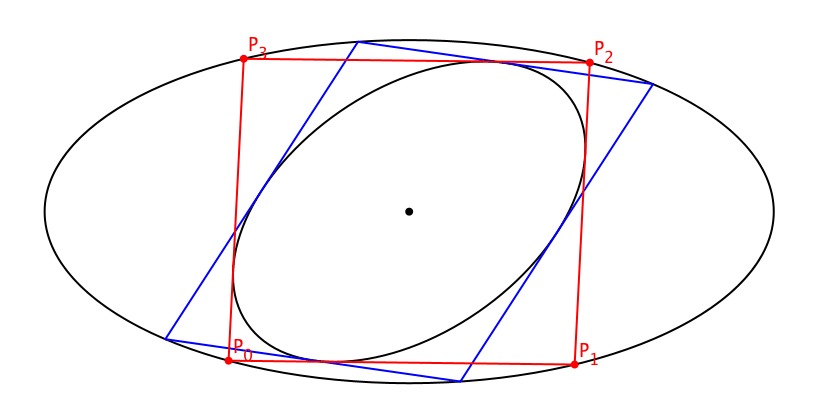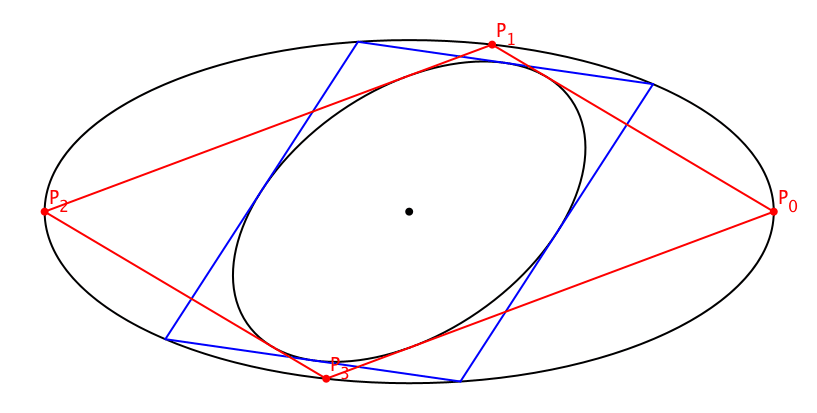
Abb. 8: Variation des Startpunktes