Hans Walser, [20100417b]
Punktsymmetrisches Sechseck
Auf jeder zweiten Seite
eines punktsymmetrischen Sechseckes setzen wir ein gleichseitiges Dreieck auf.
Dann bilden die freien Spitzen dieser Dreiecke ein ebenfalls gleichseitiges
Dreieck.
1
Spitzen nach au§en
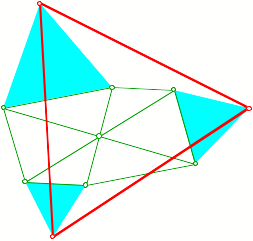
Punktsymmetrisches
Sechseck mit gleichseitigen Dreiecken
Beweis
Wir arbeiten in der
komplexen Zahlenebene und setzen den Ursprung in das Symmetriezentrum. Dann
beschriften wir gemŠ§ Figur; in der Beschriftung nźtzen wir bereits die
Punktsymmetrie aus.
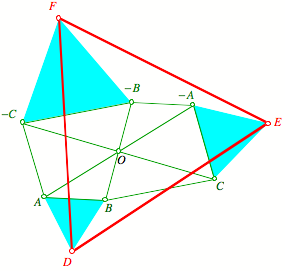
Beschriftung
Nun erhalten wir:
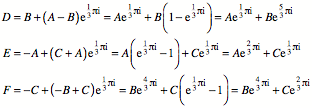
Damit wird:
![]()
Somit ist:
![]()
Das Dreieck DEF ist gleichseitig.
2
Spitzen nach innen
Der Sachverhalt gilt
auch, wenn die gleichseitigen Dreiecke nach innen gezeichnet werden.
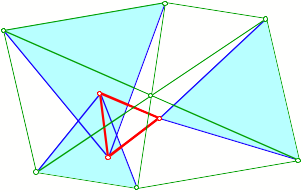
Dreiecke nach innen