Hans Walser, [20101110a]
Pyramidendach
Anregung: W. K., L. und S. R., C. Ma.
1 Das Problem
Ein Turm mit dem Grundriss eines regelmŠ§igen Sechseckes hat ein Pyramidendach.
Ich trotze Wind und Wetter
Nun regnet es schrŠg auf das Dach. Wie nass werden die DachflŠchen?
2 Bearbeitung
Wir
bearbeiten die allgemeine Situation eines Turmes mit einem regelmŠ§igen 
als Grundriss und
nummerieren die DachflŠchen mit 
.
Die aufgenommene
Wassermenge pro FlŠcheneinheit und Zeiteinheit ist proportional zum Kosinus des
Winkels zwischen dem Regenrichtungsvektor 
und dem nach
unten gerichteten Normalvektor der FlŠche. FŸr die DachflŠche mit der Nummer k haben wir den nach unten gerichteten
Normalvektor von der Form:
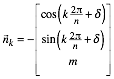
Mit dem
Neigungswinkel 
der DachflŠchen
ist 
. Weiter ist 
, unabhŠngig von k.
FŸr den
Regenrichtungsvektor 
verwenden wir die
Notation:
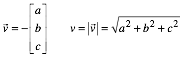
Die von der DachflŠche mit der Nummer k aufgenommene Wassermenge ist in dieser Notation proportional zu:
FŸr das gesamte Dach ergibt sich:
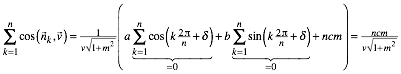
3 Nur jede zweite DachflŠche
Nun nehmen wir an, n sei eine gerade Zahl, und betrachten nur jede zweite DachflŠche, also zum Beispiel die DachflŠchen mit geraden Nummern. DafŸr erhalten wir:
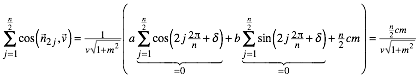
Es rauscht also genau die HŠlfte des Regens auf die DachflŠchen mit geraden Nummern, die andere HŠlfte auf die DachflŠchen mit ungeraden Nummern. Dies trotz schrŠgen Regens, dem die einzelnen DachflŠchen ganz unterschiedlich exponiert sind.
4 Verallgemeinerung
Analog
gilt allgemein: Falls 
, so erhŠlt eine regelmŠ§ige Auswahl jeder p-ten DachflŠche genau den Anteil 
des gesamten
Himmelswasser auf dem Dach. Und das trotz des schrŠgen Regens.
5 Beweisskizze
Der Witz
der Sache ist natŸrlich, dass die angegebenen Summen verschwinden. Dies kann so
eingesehen werden: Die n ebenen
Einheitsvektoren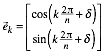 
bilden ein
regelmŠ§iges VektorenbŸschel. Zusammengesetzt ergeben sie ein geschlossenes n-Eck, die Summen der ersten wie auch
die Summen der zweiten Komponenten sind also null.
Entsprechendes gilt auch fŸr eine regelmŠ§ige Auswahl aus diesem VektorenbŸschel.
Als
Illustration die Situation fŸr 
.
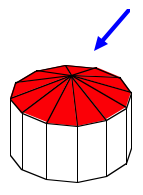
Zwšlfkant-Turm
Wenn wir alle zwšlf Vektoren nehmen, setzen sie sich zu einem regelmŠ§igen 12-Eck zusammen.
RegelmŠ§iges Zwšlfeck
Wenn wir nur jeden zweiten Vektor auswŠhlen, ergibt sich ein regelmŠ§iges Sechseck.
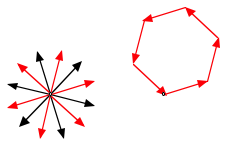
RegelmŠ§iges Sechseck
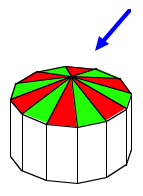
GrŸn wird gleich nass wie rot
Wenn wir nur jeden dritten Vektor auswŠhlen, erhalten wir ein Quadrat.
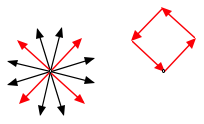
Quadrat
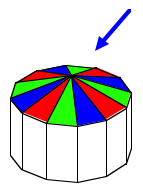
Blau wird gleich nass wie rot und wie grŸn
Wenn wir nur jeden vierten Vektor nehmen, ergibt sich ein gleichseitiges Dreieck.
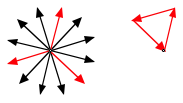
Gleichseitiges Dreieck
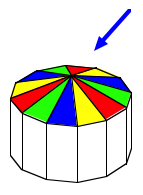
Auf allen Farben je dieselbe NŠsse
Es sei der Leserin Ÿberlassen, zu Ÿberlegen, ob und wie das weitergeht.
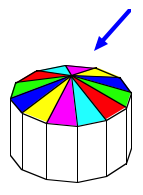
Dach in allen Farben