Hans Walser, [20040416a]

Pythagoreische Rechtecke

1 Vier gleiche rechtwinklige Dreiecke

1.1 Allgemeiner Fall

Wir starten mit einem beliebigen rechtwinkligen Dreieck in der üblichen Beschriftung.

Startdreieck

Nun versuchen wir, mit zwei solchen Dreiecken sowie ihren Spiegelbildern – insgesamt also vier kongruenten Dreiecken – ein Rechteck so auszulegen, dass an der Peripherie des Rechtecks die Seitenlängen a, b und c des Dreieckes je zwei Mal vorkommen. Dies ist – bis auf Spiegelungen – auf zwei Arten möglich.

Die beiden Lösungen

In der ersten Lösung hat das Rechteck die Länge und die Breite ; in der zweiten Lösung ist die Länge und die Breite .

In beiden Rechtecken bleibt in der Mitte ein rechteckiges „Loch“ offen, das aber offenbar dieselbe Form wie das große Recheck hat, also zum großen Rechteck ähnlich ist.

Für die erste Lösung können wir dies so einsehen: Die beiden vermuteten gleichen Seitenverhältnisse sind:

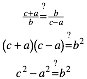
Die letzte Formelzeile ist aber nach dem Satz des Pythagoras richtig.

Für die zweite Lösung läuft der Beweis analog.

Der Verkleinerungsfaktor vom großen Rechteck zum kleinen Rechteck ist in der ersten Lösung , in der zweiten Lösung .

Im Folgenden beschränken wir uns jeweils auf die erste Lösung.

1.2 Spezielle rechtwinklige Dreiecke

1.2.1 Rechtwinklig gleichschenkliges Dreieck

Für Dreiecke mit erhalten wir Rechtecke mit dem Seitenverhältnis .

Rechtwinklige gleichschenklige Dreiecke

Ein solches Rechteck entsteht als Restrechteck, wenn wir von einem DIN A4 – Papier oben ein Quadrat abschneiden.

Von einem DIN A4 Papier wird ein Quadrat abgeschnitten

1.2.2 Goldenes Rechteck

Bei Verwendung von Dreiecken mit erhalten wir Rechtecke im goldenen Schnitt (vgl. [Steibl 1996, S. 88f], [Walser 2004, S. 39f]).

Goldene Rechtecke

2 Weiter geht’s

2.1 Wir füllen die Löcher

Da das innere Lochrechteck ähnlich ist zum großen Rechteck, können wir es analog zerlegen in vier kleinere rechtwinklige Dreiecke und ein kleineres Lochrechteck. Diese vier kleineren Figuren sind natürlich ähnlich zu den entsprechenden Ausgangsfiguren.

Weitere Unterteilung

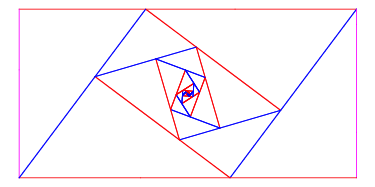
Und nun ist kein Halten mehr. Wir können die Unterteilung theoretisch ad infinitum weiterführen.

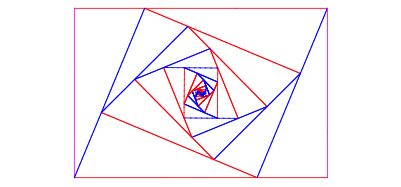
Iteration ad infinitum

2.2 Spiralen

Wenn wir uns in der Figur auf die kurzen Katheten der Dreiecke beschränken, entstehen eckige Spiralen.

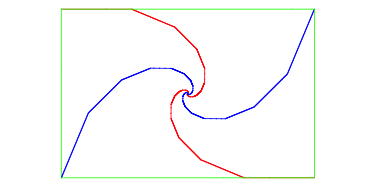
Eckige Spiralen

Die Eckpunkte dieser Spiralen liegen auf „richtigen“ logarithmischen Spiralen.

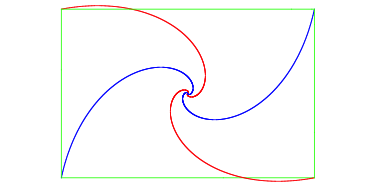
Logarithmische Spiralen

Diese vier logarithmischen Spiralen sind kongruent. Das glaubt man zuerst nicht, weil die Gesamtfigur keine vierstrahlige Rotationssymmetrie hat. Es ist aber so.

3 Pythagoreische Dreiecke

3.1 Beispiel

Bei unseren speziellen rechtwinkligen Dreiecken traten bei der Hypotenuse hässliche Wurzelausdrücke auf. Wir können dies vermeiden, wenn wir so genannte pythagoreische Dreiecke verwenden. Das sind rechtwinklige Dreiecke mit ganzzahligen Seiten. Das einfachste und am besten bekannte Beispiel ist das pythagoreische Dreieck mit den Seiten , und . Dies führt zu einem Recheck der Länge 8 und der Breite 4. Das Ding passt also, wenigstens was die Außenkontur betrifft, bestens in einen Quadratraster.

Man ist versucht, das entstehende Rechteck mit ganzzahligen Seiten als pythagoreisches Rechteck zu bezeichnen.

Pythagoreisches Recheck

Damit auch das Lochrechteck seine Eckpunkte eingerastet bekommt, ist die Maschenweite des Rasters auf einen Fünftel zu verkleinern.

Kleinerer Raster

Natürlich lässt sich auch hier das Spielchen mit der Iteration machen.

Iteration

3.2 Allgemein

Es gibt unendlich viele pythagoreische Dreiecke. Diese können wie folgt generiert werden: wir nehmen ein Zahlenpaar mit , und . Dann sind

die Seiten eines pythagoreischen Dreieckes. Die Seiten haben zudem die Eigenschaft, dass sie keinen gemeinsamen Teiler haben, wir können also nicht mehr „kürzen“.

Umgekehrt können alle pythagoreischen Dreiecke auf diese Weise gebildet werden.

Die Eingangszahlen u und v werden als Parameter des pythagoreischen Dreieckes bezeichnet. Im Dreieck sind sie allerdings nicht direkt sichtbar.

Wenn wir nun mit vier kongruenten pythagoreischen Dreiecken unser Rechteck bilden, erhalten wir ein Rechteck mit ganzzahligen Seiten, und zwar ist die Länge und die Breite . Für das Verhältnis zwischen Länge und Breite ergibt sich:

Die beiden Parameter u und v geben also das Seitenverhältnis des Rechteckes an; an diesem Rechteck werden die Parameter direkt sichtbar.

Die folgende Tabelle gibt die ersten Beispiele.

u	v	a	b	c	Länge	Breite
2	1	3	4	5	8	4
3	2	5	12	13	18	12
4	1	15	8	17	32	8
4	3	7	24	25	32	24
5	2	21	20	29	50	20
5	4	9	40	41	50	40
6	1	35	12	37	72	12
6	5	11	60	61	72	60
7	2	45	28	53	98	28
7	4	33	56	65	98	56
7	6 1	3	84	85	98	84
8	1	63	16	65	128	16
8	3	55	48	73	128	48
8	5	39	80	89	128	80
8	7	15	112	113	128	112
9	2	77	36	85	162	36
9	4	65	72	97	162	72
9	8	17	144	145	162	144
10	1	99	20	101	200	20
10	3	91	60	109	200	60
10	7	51	140	149	200	140
10	9	19	180	181	200	180

Ausmaße der pythagoreischen Rechtecke

3.3 Sonderfall Fibonacci

Die Fibonacci-Zahlen sind so definiert: Es ist eine Folge von Zahlen mit und ( so genannte Startwerte) und . Die Tabelle gibt den Anfang dieser Zahlenfolge.

Fibonacci-Folge

Zwei aufeinander folgende Fibonacci-Zahlen passen recht gut als Parameter für pythagoreische Dreiecke; allerdings ist die Bedingung bei jedem dritten Paar nicht erfüllt, nämlich dort, wo zwei ungerade Fibonacci-Zahlen aufeinander folgen. Ihre Differenz ist dann eine gerade Zahl. Wenn wir auch diese Zahlen als Parameter verwenden, erhalten wir zwar auch rechtwinklige Dreiecke mit ganzzahligen Seitenlängen, aber diese Seitenlängen haben einen gemeinsamen Teiler. Die Tabelle gibt den Anfang dieser Daten. Es ist zusätzlich das Verhältnis von Länge zu Breite der pythagoreischen Rechtecke eingetragen. Das ist, wie wir gesehen haben, das Verhältnis , in unserem Falle also:

n			a	b	c	Länge	Breite	Verhältnis
1	1	1	0	2	2	2	2	1
2	2	1	3	4	5	8	4	2
3	3	2	5	12	13	18	12	1.500000000
4	5	3	16	30	34	50	30	1.666666667
5	8	5	39	80	89	128	80	1.600000000
6	13	8	105	208	233	338	208	1.625000000
7	21	13	272	546	610	882	546	1.615384615
8	34	21	715	1428	1597	2312	1428	1.619047619
9	55	34	1869	3740	4181	6050	3740	1.617647059
10	89	55	4896	9790	10946	15842	9790	1.618181818
11	144	89	12815	25632	28657	41472	25632	1.617977528
12	233	144	33553	67104	75025	108578	67104	1.618055556
13	377	233	87840	175682	196418	284258	175682	1.618025751
14	610	377	229971	459940	514229	744200	459940	1.618037135
15	987	610	602069	1204140	1346269	1948338	1204140	1.618032787

Pythagoreische Rechtecke mit Fibonacci-Zahlen

Wir sehen, dass sich das Seitenverhältnis der pythagoreischen Dreiecke einem bestimmten Wert annähert; dies ist der goldene Schnitt . Die ist weiter nicht überraschend, denn dies gilt bereits für das Verhältnis aufeinander folgender Fibonacci-Zahlen.

Andererseits hatten wir das goldene Rechteck bereits erhalten unter Verwendung des Dreieckes mit . Dies heißt nun aber, dass die in der Tabelle aufgelisteten pythagoreischen Dreiecke dieses spezielle Dreieck mit approximieren. Tatsächlich gilt etwa für das Verhältnis:

Literatur

[Steibl 1996] Steibl, Horst: Geometrie aus dem Zettelkasten. Hildesheim: Franzbecker 1996. ISBN 3-88120-269-2

[Walser 2004] Walser, Hans: Der Goldene Schnitt. 4. Auflage. Leipzig: Edition am Gutenbergplatz 2004. ISBN 3-937219-00-5