Hans Walser, [20180326]

Pythagoreische Dreiecke falten

Anregung: R. S.-H., F.

1 Worum geht es

Durch Falten erhalten wir eine Folge von pythagoreischen Dreiecken. Es ergibt sich auch eine Verallgemeinerung des Satzes von Haga.

2 Das Vorgehen

Wir arbeiten mit quadratischem Origami-Papier der Kantenlänge 1. Vorderseite gelb, Rückseite zyan. Durch Falten finden wir den Mittelpunkt der Oberkante (Abb. 1).

Abb. 1: Mittelpunkt der Oberkante

Wir falten nun den rechten unteren Eckpunkt auf diesen Mittelpunkt (Abb. 2).

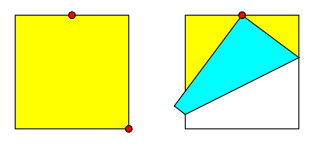
Abb. 2: Rechte untere Ecke

Es werden zwei gelbe rechtwinklige Dreiecke sichtbar. Im Dreieck rechts oben haben wir für die längere Kathete:

(1)

Wegen

(2)

und

(3)

folgt:

(4)

Somit ist:

(5)

Es handelt sich um das „Lehrer-Dreieck“, das einfachste pythagoreische Dreieck.

Das Dreieck links oben ist dazu ähnlich. Daher ergeben sich die Längen gemäß Abbildung 3 (Satz von Haga).

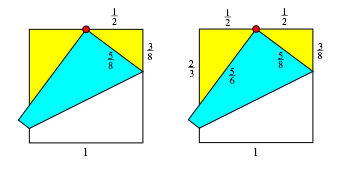
Abb. 3: Satz von Haga

Nun falten wir die beiden in der Abbildung 4 blau markierten Punkte aufeinander. Dadurch erhalten wir ein neues rechtwinkliges Dreieck mit der langen Kathete:

(6)

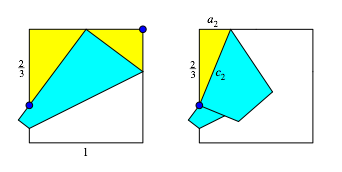
Abb. 4: Neues rechtwinkliges Dreieck

Wegen

(7)

und

(8)

ergibt sich:

(9)

Wir haben also das pythagoreische Dreieck mit dem Seitenverhältnis:

(10)

Die Abbildung 5 zeigt die beiden nächsten Faltschritte. Es wird aufgefaltet.

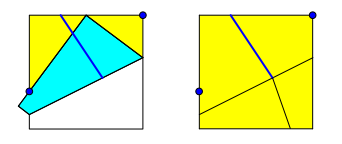
Abb. 5: Auffalten

Nun falten wir erneut die beiden blauen Punkte aufeinander und falten anschließend die beiden roten Punkte aufeinander (Abb. 6).

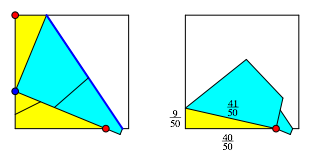
Abb. 6: Nächster Faltschritt

So entsteht ein weiteres rechtwinkliges Dreieck. Mit einer analogen Rechnung wie oben erhalten wir:

(11)

Wir haben also das pythagoreische Dreieck mit dem Seitenverhältnis:

(12)

Wir vermuten, dass wir durch Iteration eine Folge von pythagoreischen Dreiecken erhalten.

3 Rekursion

Die Abbildung 7 illustriert den allgemeinen Iterationsschritt von auf .

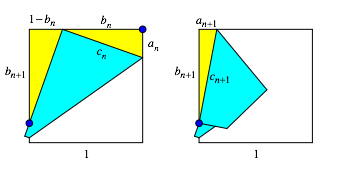
Abb. 7: Allgemeiner Schritt

Wir erhalten zunächst:

(13)

Aus

(14)

und

(15)

ergibt sich

(16)

und:

(17)

Mit den Formeln (13), (16) und (17) ist die Rekursion vollständig beschrieben.

4 Tabellen

Die Tabelle 1 gibt die ersten 10 Beispiele.

n	an	bn	cn
1	3/8	1/2	5/8
2	5/18	2/3	13/18
3	9/50	4/5	41/50
4	17/162	8/9	145/162
5	33/578	16/17	545/578
6	65/2178	32/33	2113/2178
7	129/8450	64/65	8321/8450
8	257/33282	128/129	33025/33282
9	513/132098	256/257	131585/132098
10	1025/526338	512/513	525313/526338

Tab. 1: Beispiele

In der Spalte für b_n sehen wir die Verallgemeinerung des Satzes von Haga. Offenbar ist:

(18)

Weiter ist:

(19)

In der Tabelle 2 sind die Seitenverhältnisse in ganzen Zahlen angegeben. Der Querstrich deutet diese Erweiterung an. Es sind alles pythagoreische Dreiecke. Zusätzlich sind die Parameter u und v dieser pythagoreischen Dreiecke angegeben.

n				un	vn
1	3	4	5	2	1
2	5	12	13	3	2
3	9	40	41	5	4
4	17	144	145	9	8
5	33	544	545	17	16
6	65	2112	2113	33	32
7	129	8320	8321	65	64
8	257	33024	33025	129	128
9	513	131584	131585	257	256
10	1025	525312	525313	513	512

Tab. 2: Ganzzahlige Seitenverhältnisse

Zur Erinnerung: Zu teilerfremden u > v > 1, mod(u – v, 2) = 1, sind

(20)

die Seiten eines primitiven pythagoreischen Dreieckes. Diese Parametrisierung ist eindeutig.

5 Feststellungen

Auf Grund der Tabelle 2 vermuten wir:

(21)

Weiter ist:

(22)

Durch Nachrechnen zeigt man, dass (22) mit (20) und (21) kompatibel ist.

Die lange Kathete und die Hypotenuse unterscheiden sich nur um 1:

(23)

Die Dreiecke sind also fast gleichschenklig, mit einer vergleichsweise kurzen Basis a_n.

6 Beweis

Wir haben zu zeigen, dass wir bei Fortführung des Faltprozesses eine unendliche Folge von pythagoreischen Dreiecken erhalten. Dazu setzen wir:

(24)

Damit lassen sich vermöge (20) die ganzzahligen Werte berechnen:

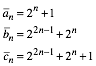(25)

Daraus ergibt sich die Hilfsgröße:

(26)

Für die Berechnung der ursprünglich durch Falten erhaltenen Werte a_n, b_n, c_n müssen die Werte aus (25) so skaliert werden, dass a_n + c_n = 1 wird (Seitenlänge des Origami-Papieres). Also:

(27)

Zu zeigen ist nun folgendes: Die Werte (27) genügen den Rekursionsformeln (13), (16) und (17). Der Autor hat das mit CAS verifiziert.

7 Der Winkel alpha

In der Tabelle 3 sind zusätzlich die der Seite a_n gegenüberliegenden Winkel in ° sowie deren Partialsummen angegeben.

n
1	3	4	5	36.86989765°	36.86989765°
2	5	12	13	22.61986495°	59.48976260°
3	9	40	41	12.68038349°	72.17014609°
4	17	144	145	6.732921330°	78.90306742°
5	33	544	545	3.471409177°	82.37447660°
6	65	2112	2113	1.762807993°	84.13728459°
7	129	8320	8321	0.8882888659°	85.02557346°
8	257	33024	33025	0.4458793023°	85.47145276°
9	513	131584	131585	0.2233750757°	85.69482784°
10	1025	525312	525313	0.1117966075°	85.80662445°

Tab. 3: Winkel alpha

Wir sehen, dass diese Winkel in etwa wie eine geometrische Folge mit q = ½ abnehmen. Ich vermute daher, dass die Partialsummenfolge konvergiert.