Hans Walser, [20110613a]
Pythagoreische Dreiecke
Anregungen: M. B., B. und A. R., S.
1 Worum geht es?
Es wird versucht, einige Eigenschaften der Pythagoreischen Zahlentripel und der pythagoreischen Dreiecke zu visualisieren.
2 Formeln
2.1 Generierung der pythagoreischen Zahlentripel
In der Regel werden die pythagoreischen Zahlentripel wie folgt generiert:
Wir wŠhlen zwei natźrliche Zahlen (Parameter) u und v mit folgenden Bedingungen:
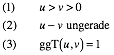
Dann setzen wir:
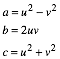
a, b und c bilden ein primitives (teilerfremdes) pythagoreisches Zahlentripel. Auf diese Weise ergeben sich alle primitiven pythagoreischen Zahlentripel ([Dickson 1920] und [Dickson 1966]).
Die Bedingung (1) sichert, dass a, b, c positiv sind. Wenn wir auf die Bedingung (1) verzichten, mźssen wir mit den BetrŠgen von a, b, c arbeiten, um ein Dreieck zeichnen zu kšnnen. Wir werden das im folgenden gelegentlich tun.
Wenn die Bedingung (2) verletzt ist, haben a, b, c den gemeinsamen Teiler 2.
Wenn die
Bedingung (3) verletzt ist, haben a, b, c
den gemeinsamen Teiler ![]() .
.
Wenn wir also zulassen, dass a, b, c gemeinsame Teiler haben, kšnnen wir auf die EinschrŠnkungen (2) und (3) verzichten. Wir werden das im folgenden gelegentlich tun.
2.2 Umkehrung
Umgekehrt gelten die Formeln:
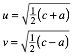
2.3 In- und Ankreisradien
Inkreisradius:
![]()
Ankreisradien:
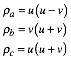
Diese Radien sind ebenfalls natźrlich Zahlen (vgl. [Baptist 1982]). Bei den Formeln fźr die Radien ist nicht recht einsichtig, warum der Inkreisradius eine Sonderrolle spielen soll.
Wenn wir
auf die Bedingung ![]() verzichten,
mźssen wir mit den BetrŠgen arbeiten.
verzichten,
mźssen wir mit den BetrŠgen arbeiten.
3 Darstellung im Koordinatensystem
3.1 Das Dreieck
In einem kartesischen Koordinatensystem wŠhlen wir die Eckpunkte A, B, C der pythagoreischen Dreiecke wie folgt:
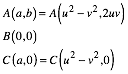
Die
Koordinaten sind ganzzahlig. Wenn wir auf die Bedingung ![]() verzichten,
kšnnen sie negativ sein.
verzichten,
kšnnen sie negativ sein.
Fźr den Mittelpunkt M des Umkreises (Thaleskreis) ergibt sich:
![]()
3.2 Zentren von In- und Ankreisen
Zentrum des Inkreises:
![]()
Zentren der Ankreise:
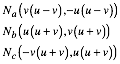
Bemerkung: Der Schwerpunkt dieser vier Punkte ist der Mittelpunkt M des Umkreises. Dies gilt allerdings in einem beliebigen Dreieck.
Bei den Formeln fźr die Zentren ist nicht recht einsichtig, warum der Inkreis eine Sonderrolle spielen soll.
3.3 Der W-Punkt
Wir
definieren den Punkt ![]() . Er illustriert die beiden Parameter.
. Er illustriert die beiden Parameter.
3.4 Beispiel
Die
Abbildung 1 zeigt den Fall fźr ![]() . Dieser Punkt ist grźn eingezeichnet. Es ist weiter:
. Dieser Punkt ist grźn eingezeichnet. Es ist weiter:
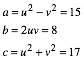
Fźr den Inkreisradius erhalten wir:
![]()
Ankreisradien:
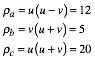
Zentrum des Inkreises:
![]()
Zentren der Ankreise:
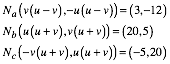
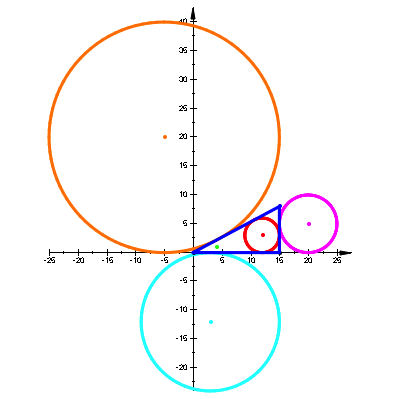
Abb. 1: u = 4, v = 1
3.5 In der Gau§schen Zahlenebene
Mit ![]() erhalten wir
zunŠchst den Punkt W. Wegen
erhalten wir
zunŠchst den Punkt W. Wegen
![]()
ergibt
sich durch ![]() der Punkt A. Aus den Regeln des Rechnens mit den
komplexen Zahlen folgt, dass der Punkt W
auf der Winkelhalbierenden des Winkels
der Punkt A. Aus den Regeln des Rechnens mit den
komplexen Zahlen folgt, dass der Punkt W
auf der Winkelhalbierenden des Winkels ![]() liegt.
liegt.
4 Ausdehnung des Parameterbereiches
Wir
verzichten nun ausdrźcklich auf die einschrŠnkende Bedingung ![]() . Es soll nun also
. Es soll nun also ![]() .
.
Wir illustrieren die Situation an den acht Beispielen (Abb. 2):
![]()
Der grźne
Punkt ![]() gibt jeweils die
aktuellen Parameter an.
gibt jeweils die
aktuellen Parameter an.
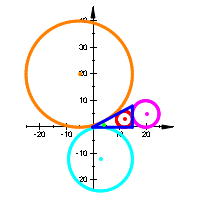
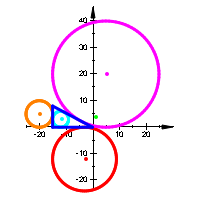
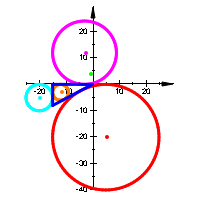
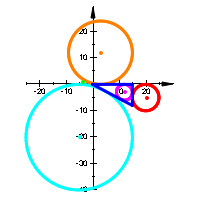
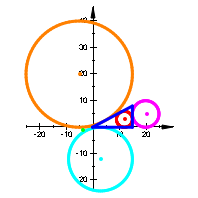
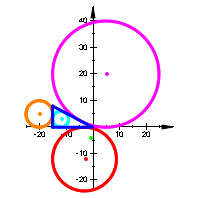
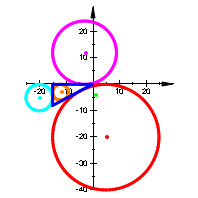
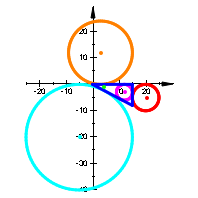
Abb. 2: Permutation der Parameter und Vorzeichen
Wir sehen, dass die Rollen der In- und Ankreise permutiert werden.
5 Visualisierung einzelner Punkte
5.1 Die Punkte W
Wir zeichnen
die Punkte ![]() mit gźner
Quadratsignatur der SeitenlŠnge 1.
mit gźner
Quadratsignatur der SeitenlŠnge 1.
Die
Bedingung ![]() fźhrt zu einem
etwas langweiligen Bild. Fźr die Abbildung 3 ist
fźhrt zu einem
etwas langweiligen Bild. Fźr die Abbildung 3 ist ![]() .
.
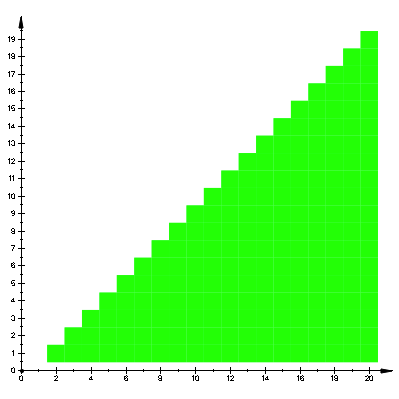
Abb. 3: u > v > 0
Mit den beiden
Bedingungen ![]() ergibt sich ein
Karo-Muster (Abb. 4).
ergibt sich ein
Karo-Muster (Abb. 4).
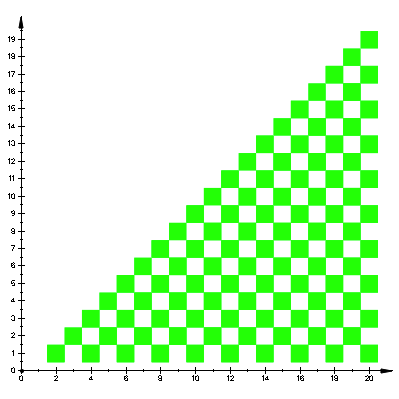
Abb. 4: Karo-Muster
Mit den
beiden Bedingungen ![]() wird es
spannender (Abb. 5).
wird es
spannender (Abb. 5).
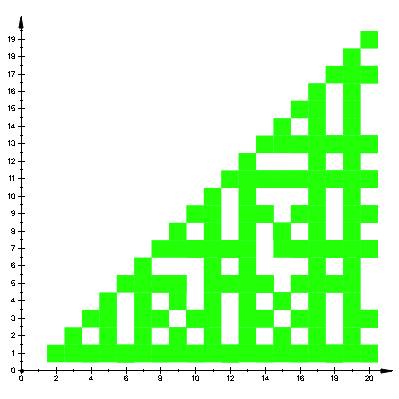
Abb. 5: u und v teilerfremd
Die Prinzahlen fźhren zu einer durchgehenden horizontalen oder vertikalen Linie. Deutlich sind auch die Primzahlzwillinge (zum Beispiel 11 / 13 oder 17 / 19) zu erkennen.
Das
Muster wird noch interessanter, wenn wir auf die EinschrŠnkung ![]() verzichten. Fźr
die Abbildung 6 ist
verzichten. Fźr
die Abbildung 6 ist ![]() .
.

Abb. 6: u und v teilerfremd
Jede
horizontale und jede vertikale Linie hat eine Translationssymmetrie. Als
Beispiel etwa die horizontalen Linien fźr ![]() (Abb. 7).
(Abb. 7).

Abb. 7: v = 5, 10, 15
Und nun
alle drei Bedingungen, also ![]() . Wir erhalten so
die Punkte W (Abb. 8).
. Wir erhalten so
die Punkte W (Abb. 8).
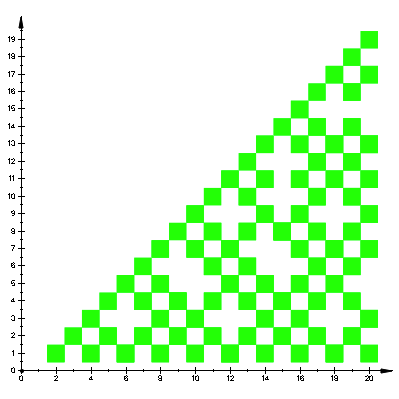
Abb. 8: Die Punkte W
Die
Primzahlen und insbesondere die Primzahlzwillingen sind nun als schrŠge Linien
(mit den Steigungen ![]() ) erkennbar.
) erkennbar.
Im der
Abbildung 8 ist die Bedingung ![]() weggelassen. Es
ist
weggelassen. Es
ist ![]() .
.

Abb. 9: Bedingungen (2) und (3)
5.2 Die Punkte A
Der Punkt
A ist gegeben durch ![]() . Wir stellen die Punkte mit blauer Kreissignatur dar.
. Wir stellen die Punkte mit blauer Kreissignatur dar.
ZunŠchst
verwenden wir nur die Bedingung ![]() . Das ergibt ein ăgebogenesŇ Raster. In der Abbildung 10 ist
. Das ergibt ein ăgebogenesŇ Raster. In der Abbildung 10 ist ![]() .
.
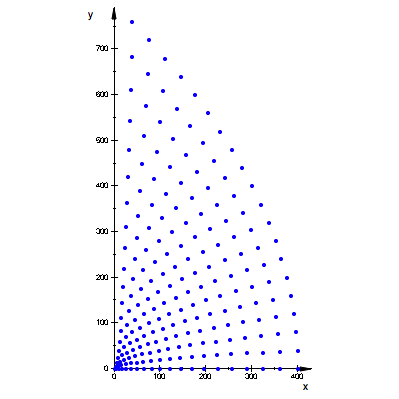
Abb. 10: Gebogenes Raster
Um die
Struktur des Rasters zu erkennen, lassen wir die Bedingung ![]() auch noch weg. In
der Abbildung 11 ist
auch noch weg. In
der Abbildung 11 ist ![]() . Die Punkte sind die Schnittpunkte von konfokalen liegenden
Parabeln. Darin zeigt sich, dass hinter unseren Formeln die komplexe
Quadratfunktion steckt. Die komplexe Quadratfunktion fźhrt zu einer doppelten
†berlagerung. Jede Punkt ist doppelt gezeichnet.
. Die Punkte sind die Schnittpunkte von konfokalen liegenden
Parabeln. Darin zeigt sich, dass hinter unseren Formeln die komplexe
Quadratfunktion steckt. Die komplexe Quadratfunktion fźhrt zu einer doppelten
†berlagerung. Jede Punkt ist doppelt gezeichnet.

Abb. 11: Liegende Parabeln
Nun
bringen wir die Bedingung ![]() ins Spiel (Abb.
12). Wir erhalten wieder Parabeln, diese sind nun wie in der Schule
ăstehendŇ. Warum ist das so?
ins Spiel (Abb.
12). Wir erhalten wieder Parabeln, diese sind nun wie in der Schule
ăstehendŇ. Warum ist das so?
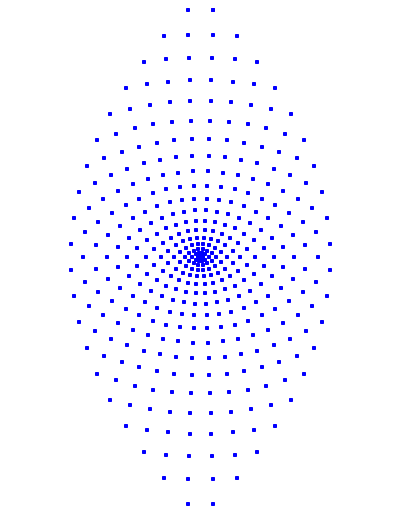
Abb. 12: Stehende Parabeln
Die
Bedingung ![]() bringt zusŠtzlich
eine Ausdźnnung (Abb. 13).
bringt zusŠtzlich
eine Ausdźnnung (Abb. 13).
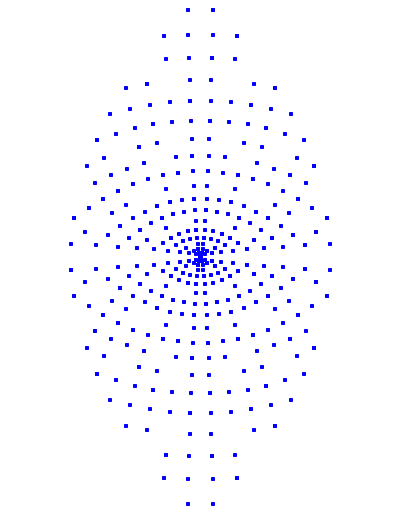
Abb. 13: Bedingungen (2) und (3)
5.3 Die Inkreismittelpunkte N
Fźr die
Inkreismittelpunkt N gilt ![]() . Wir arbeiten zunŠchst ohne Bedingungen. In der Abbildung 14
ist
. Wir arbeiten zunŠchst ohne Bedingungen. In der Abbildung 14
ist ![]() .
.

Abb. 14: Na schšn
Die
Bedingung ![]() dźnnt aus (Abb.
15).
dźnnt aus (Abb.
15).

Abb. 15: Bedingung (2)
Die
Bedingung ![]() bringt eine
zusŠtzliche Ausdźnnung (Abb. 16).
bringt eine
zusŠtzliche Ausdźnnung (Abb. 16).

Abb. 16: Bedingungen (2) und (3)
5.4 Ankreismittelpunkte
Fźr die Ankreismittelpunkte gelten die Formeln:
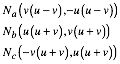
In den
folgenden Abbildungen sind die Punkte ![]() cyan,
cyan, ![]() magenta und
magenta und ![]() orange
gezeichnet. ZusŠtzlich sind die Inkreismittelpunkte (rot) eingezeichnet.
orange
gezeichnet. ZusŠtzlich sind die Inkreismittelpunkte (rot) eingezeichnet.
Wenn wir
ohne weitere Bedingungen arbeiten, erhalten wir fźr ![]() die Abbildung 17.
Auf den ersten Blick verblźffend ist die vierteilige Drehsymmetrie.
die Abbildung 17.
Auf den ersten Blick verblźffend ist die vierteilige Drehsymmetrie.

Abb. 17: Ohne EinschrŠnkung
In der Abbildung 18 sind zusŠtzlich noch die Punkte A eingezeichnet.
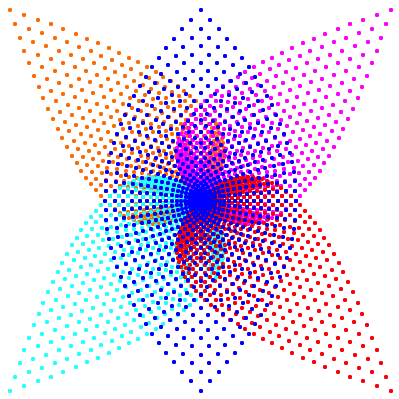
Abb. 18: ZusŠtzlich mit Punkten A
In der
Abbildung 19 sind die beiden Bedingungen ![]() eingearbeitet.
eingearbeitet.
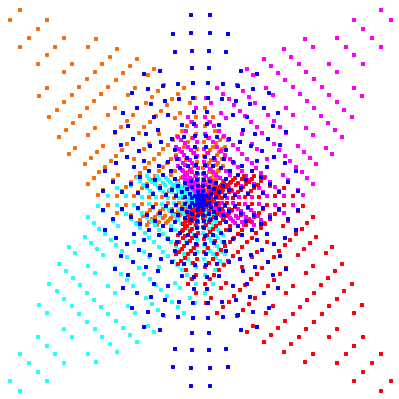
Abb. 19: In- und Ankreismittelpunkte sowie Punkte A
Literatur
[Baptist 1982] Baptist, P.: Inkreisradius und pythagoreische Zahlentripel. Praxis der Mathematik 24, 1982, S. 161 - 164.
[Dickson 1920] Dickson, Leonard Eugene: History of the Theory of Numbers, II. Diophantine Analysis. Washington: Carnegie Institution 1920.
[Dickson 1966] Dickson, Leonard Eugene: History of the Theory of Numbers; vol II. New York: Chelsea 1966.