Hans Walser, [20191103]

Pythagoreische Dreiecke

1 Worum geht es?

Geometrischer Zugang zu den pythagoreischen Dreiecken.

2 Klassisch

Der klassische Zugang zu den primitiven (Seiten teilerfremd) pythagoreischen Dreiecken geht rechnerisch. Wir wählen die beiden Parameter u und v mit folgenden Bedingungen: u > v, u, v teilerfremd und u – v ungerade. Dann sind

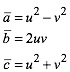(1)

die Seiten eines primitiven pythagoreischen Dreieckes. Umgekehrt lässt sich jedes primitive pythagoreische Dreieck auf diese Weise parametrisieren.

3 Geometrischer Zugang

Wir zeichnen ein Rechteck mit den Seitenlängen u und v (Abb. 1). In diesem Rechteck zeichnen wir eine Diagonale und deren Mittelsenkreche. Die Mittelsenkrechte schneiden wir mit der langen Rechteckseite.

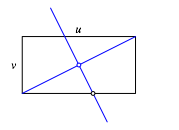
Abb. 1: Rechteck und Mittelsenkrechte der Diagonale

Der Schnittpunkt bildet zusammen mit zwei Rechteckecken das gesucht pythagoreische Dreieck (Abb. 2).

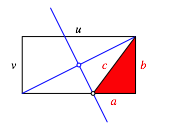
Abb. 2: Pythagoreisches Dreieck

4 Beweis

4.1 Von den Parametern zum Dreieck

Wir arbeiten im kartesischen Koordinatensystem der Abbildung 3 und berechnen die Streckenlänge d.

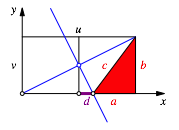
Abb. 3: Koordinatensystem

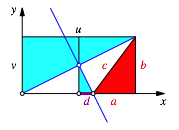
Abb. 4: Ähnlichkeit

Auf Grund der Ähnlichkeit (Abb. 4) erhalten wir:

(2)

Daraus ergibt sich:

(3)

Weiter ist:

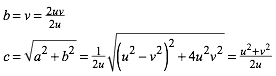(4)

Aus (3) und (4) ergibt sich die Kompatibilität mit (1).

4.2 Umkehrung: vom Dreieck zu den Parametern

Mit einem gegebenen pythagoreischen Dreieck und drei Kopien (zwei davon spiegelbildlich) bilden wir das Rechteck gemäß Abbildung 5. Das Rechteck hat ein rechteckiges Loch. (Das Lochrechteck ist ähnlich zum gesamten Rechteck.)

Abb. 5: Rechteck aus vier Dreiecken

Die Seitenlängen sind ganzzahlig. Gekürzt ergeben sie u und v. Die Abbildung 5 gehört zum Beispiel u = 2 und v = 1 (so genanntes „Lehrerdreieck“).