1 Worum geht es?

Geometrischer Zugang zu den pythagoreischen Dreiecken.

2 Klassisch

Der klassische Zugang zu den primitiven (Seiten teilerfremd) pythagoreischen Dreiecken geht rechnerisch. Wir wählen die beiden Parameter u und v mit folgenden Bedingungen: u > v, u, v teilerfremd und u – v ungerade. Dann sind

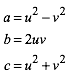(1)

die Seiten eines primitiven pythagoreischen Dreieckes. Umgekehrt lässt sich jedes primitive pythagoreische Dreieck auf diese Weise parametrisieren.

Die Tabelle 1 zeigt die ersten Werte.

u	v	a	b	c
2	1	3	4	5
3	2	5	12	13
4	1	15	8	17
4	3	7	24	25
5	2	21	20	41
5	4	9	40	41

Tab. 1: Pythagoreische Tripel

3 Geometrischer Zugang

3.1 Beispiel

Für u = 2 und v = 1 ergibt sich das pythagoreische Dreieck mit den Seiten a = 3, b = 4 und c = 5.

Wir konstruieren nun ein Dreieck mit diesem Seitenverhältnis wie folgt.

Wir zeichnen den Einheitskreis (Abb. 1a) und anschließend ein rechtwinkliges Dreieck mit den Katheten u = 2 und v = 1 in der Position der Abbildung 1b.

Abb. 1: Kreis und Dreieck

Nun schneiden wir die Hypotenuse dieses rechtwinkligen Dreiecks mit dem Einheitskreis (Abb. 2a).

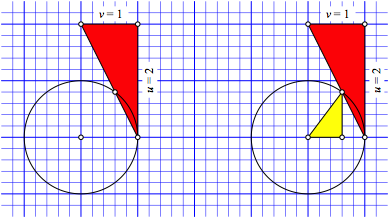
Abb. 2: Schnittpunkt und pythagoreisches Dreieck

Wir können nun im Einheitskreis ein rechtwinkliges Dreieck einzeichnen (Abb. 2b). Dieses hat das Seitenverhältnis 3:4:5, ist also das gesuchte pythagoreische Dreieck.

3.2 Allgemein und Beweis

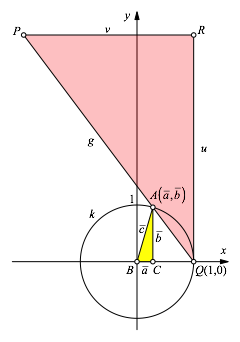
Wir arbeiten mit den Bezeichnungen der Abbildung 3.

Abb. 3: Beweisfigur

Der Einheitskreis hat die Gleichung:

(2)

Für die Gerade g erhalten wir die Gleichung:

(3)

Für die Koordinaten und des Schnittpunktes A erhalten wir aus (2) und (3):

(4)

Es ist also:

(5)

Dies war zu zeigen.

Literatur

Baptist, Peter (1982): Inkreisradius und pythagoreische Zahlentripel. Praxis der Mathematik, 24, 161-164.

Dickson, Leonard Eugene (1920): History of the Theory of Numbers, II. Diophantine Analysis. Washington: Carnegie Institution.

Dickson, Leonard Eugene (1966): History of the Theory of Numbers; vol II. New York: Chelsea.

Foster, Colin (2016): Proof Without Words: Integer Right Triangle Hypotenuses Without Pythagoras. The College Mathematics Journal. Vol. 47, No. 2, March 2016, 101.

Sierpiński, Wacław (1962): Pythagorean Triangles. Trans. A. Sharma. Yeshiva Univ., New York, 1962. Reprinted by Dover, Minneola, NY, 2003.

Websites

Hans Walser: Pythagorean Traingles

http://www.walser-h-m.ch/hans/Miniaturen/P/Pythagorean_Triangles/Pythagorean_Triangles.htm

http://www.walser-h-m.ch/hans/Miniaturen/P/Pythagorean_Triangles/Pythagorean_Triangles.pdf

Hans Walser: Pythagoreische 60°- und 120°-Dreiecke

http://www.walser-h-m.ch/hans/Miniaturen/P/Pyth-60-Dreiecke/Pyth-60-Dreiecke.htm

http://www.walser-h-m.ch/hans/Miniaturen/P/Pyth-60-Dreiecke/Pyth-60-Dreiecke.pdf

Hans Walser: Pythagoreische Dreiecke

http://www.walser-h-m.ch/hans/Miniaturen/P/Pyth_Dreiecke/Pyth_Dreiecke.htm

http://www.walser-h-m.ch/hans/Miniaturen/P/Pyth_Dreiecke/Pyth_Dreiecke.pdf

Hans Walser: Pythagoreische Dreiecke