1 Worum geht es?

Visualisierung der üblichen Parametrisierung der pythagoreischen Dreiecke.

2 Erinnerung

Mit

$Titel: {"mathml":"<math style=\"font-family:stix;font-size:24px;\" xmlns=\"http://www.w3.org/1998/Math/MathML\"><mstyle mathsize=\"24px\"><mi>u</mi><mo>,</mo><mi>v</mi><mo>∈</mo><mi mathvariant=\"normal\">ℕ</mi><mo>,</mo><mo/><mi>u</mi><mo>></mo><mi>v</mi><mo>></mo><mn>0</mn><mo>,</mo><mo/><mi>gcd</mi><mfenced><mrow><mi>u</mi><mo>,</mo><mi>v</mi></mrow></mfenced><mo>=</mo><mn>1</mn><mo>,</mo><mo/><mi>mod</mi><mfenced><mrow><mi>u</mi><mo>-</mo><mi>v</mi><mo>,</mo><mo/><mn>2</mn></mrow></mfenced><mo>=</mo><mn>1</mn></mstyle></math>"} - Beschreibung: u Komma v element von gerade natürliche Zahlen Komma u größer als v größer als 0 Komma gcd Klammer öffnen u Komma v Klammer schließen gleich 1 Komma mod Klammer öffnen u minus v Komma 2 Klammer schließen gleich 1$

ist

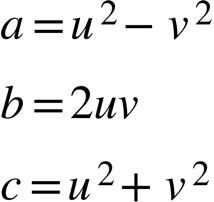
$Titel: {"mathml":"<math style=\"font-family:stix;font-size:24px;\" xmlns=\"http://www.w3.org/1998/Math/MathML\"><mstyle mathsize=\"24px\"><mi>a</mi><mo>=</mo><msup><mi>u</mi><mn>2</mn></msup><mo>-</mo><msup><mi>v</mi><mn>2</mn></msup><mspace linebreak=\"newline\"/><mi>b</mi><mo>=</mo><mn>2</mn><mi>u</mi><mi>v</mi><mspace linebreak=\"newline\"/><mi>c</mi><mo>=</mo><msup><mi>u</mi><mn>2</mn></msup><mo>+</mo><msup><mi>v</mi><mn>2</mn></msup></mstyle></math>"} - Beschreibung: a gleich u im Quadrat minus v im Quadrat b gleich 2 u v c gleich u im Quadrat plus v im Quadrat$

ein primitives pythagoreisches Tripel.

3 Form des pythagoreischen Dreieckes

Die Form des zugehörigen pythagoreischen Dreieckes (gelb) kann in der Figur der Abbildung 1 (für u = 3 und v = 2) gesehen werden.

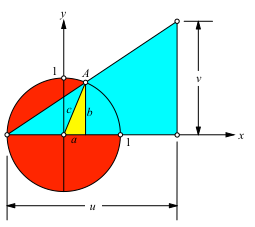
Abb. 1: Gelbes pythagoreisches Dreieck

4 Nachweis

Der rote Einheitskreis hat die Gleichung:

$Titel: {"mathml":"<math style=\"font-family:stix;font-size:24px;\" xmlns=\"http://www.w3.org/1998/Math/MathML\"><mstyle mathsize=\"24px\"><msup><mi>x</mi><mn>2</mn></msup><mo>+</mo><msup><mi>y</mi><mn>2</mn></msup><mo>=</mo><mn>1</mn></mstyle></math>"} - Beschreibung: x im Quadrat plus y im Quadrat gleich 1$

Die schräge Hypotenuse des hellblauen Dreiecks hat die Gleichung:

$Titel: {"mathml":"<math style=\"font-family:stix;font-size:24px;\" xmlns=\"http://www.w3.org/1998/Math/MathML\"><mstyle mathsize=\"24px\"><mi>y</mi><mo>=</mo><mfrac><mi>v</mi><mi>u</mi></mfrac><mo>+</mo><mfrac><mi>v</mi><mi>u</mi></mfrac><mi>x</mi></mstyle></math>"} - Beschreibung: y gleich v geteilt durch u plus v geteilt durch u x$

Damit ergeben sich für den Schnittpunkt A die Koordinaten:

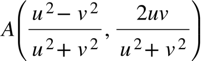
$Titel: {"mathml":"<math style=\"font-family:stix;font-size:24px;\" xmlns=\"http://www.w3.org/1998/Math/MathML\"><mstyle mathsize=\"24px\"><mi>A</mi><mfenced><mrow><mfrac><mrow><msup><mi>u</mi><mn>2</mn></msup><mo>-</mo><msup><mi>v</mi><mn>2</mn></msup></mrow><mrow><msup><mi>u</mi><mn>2</mn></msup><mo>+</mo><msup><mi>v</mi><mn>2</mn></msup></mrow></mfrac><mo>,</mo><mo/><mfrac><mrow><mn>2</mn><mi>u</mi><mi>v</mi></mrow><mrow><msup><mi>u</mi><mn>2</mn></msup><mo>+</mo><msup><mi>v</mi><mn>2</mn></msup></mrow></mfrac></mrow></mfenced></mstyle></math>"} - Beschreibung: A Klammer öffnen Zähler u im Quadrat minus v im Quadrat geteilt durch Nenner u im Quadrat plus v im Quadrat Bruchergebnis Komma Zähler 2 u v geteilt durch Nenner u im Quadrat plus v im Quadrat Bruchergebnis Klammer schließen$

Somit ist:

$Titel: {"mathml":"<math style=\"font-family:stix;font-size:24px;\" xmlns=\"http://www.w3.org/1998/Math/MathML\"><mstyle mathsize=\"24px\"><mi>a</mi><mo>:</mo><mi>b</mi><mo>:</mo><mi>c</mi><mo>=</mo><mfenced><mrow><msup><mi>u</mi><mn>2</mn></msup><mo>-</mo><msup><mi>v</mi><mn>2</mn></msup></mrow></mfenced><mo>:</mo><mfenced><mrow><mn>2</mn><mi>u</mi><mi>v</mi></mrow></mfenced><mo>:</mo><mfenced><mrow><msup><mi>u</mi><mn>2</mn></msup><mo>+</mo><msup><mi>v</mi><mn>2</mn></msup></mrow></mfenced></mstyle></math>"} - Beschreibung: a Doppelpunkt b Doppelpunkt c gleich Klammer öffnen u im Quadrat minus v im Quadrat Klammer schließen Doppelpunkt Klammer öffnen 2 u v Klammer schließen Doppelpunkt Klammer öffnen u im Quadrat plus v im Quadrat Klammer schließen$

Dies war zu zeigen.

Websites

Hans Walser: Pythagorean Triangles

http://www.walser-h-m.ch/hans/Miniaturen/P/Pythagorean_Triangles/Pythagorean_Triangles.htm

Hans Walser: Pythagoreische Dreiecke

http://www.walser-h-m.ch/hans/Miniaturen/P/Pyth_Dreiecke/Pyth_Dreiecke.htm

Hans Walser: Pythagoreische Dreiecke

http://www.walser-h-m.ch/hans/Miniaturen/P/Pyth_Dreiecke2/Pyth_Dreiecke2.htm

Hans Walser: Pythagoreische Dreiecke

http://www.walser-h-m.ch/hans/Miniaturen/P/Pyth_Dreiecke3/Pyth_Dreiecke3.htm

Hans Walser: Pythagoreische Dreiecke

http://www.walser-h-m.ch/hans/Miniaturen/P/Pyth_Dreiecke4/Pyth_Dreiecke4.htm

Hans Walser: Pythagoreische Dreiecke falten

http://www.walser-h-m.ch/hans/Miniaturen/P/Pyth_Dr_falten/Pyth_Dr_falten.htm