Hans Walser, [20120616]
Pythagoreische Vierecke
1
Problemstellung
Genau in den Vierecken mit orthogonalen Diagonalen gilt:
Gesucht sind
nichttriviale ganzzahlige Lšsungen dieser Gleichung. Triviale Lšsungen sind 
(Rhombus) und 
oder 
(Drachenviereck).
2
Beispiel
Die Abbildung zeigt ein
solches Viereck.
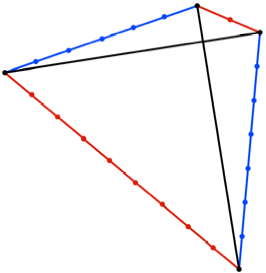
Viereck
Das Viereck ist durch
seine vier Seiten nicht eindeutig bestimmt. Die Diagonalen sind immer
orthogonal, die DiagonalenlŠngen sind offen und in der Regel nicht ganzzahlig.
Fragen:
á
Gibt es Vierecke, bei denen beide DiagonalenlŠngen
ganzzahlig sind?
á
Gibt es Vierecke, bei denen alle vier
Diagonalenabschnitte ganzzahlig sind?
3
Allgemein
Umformung:
Wir mźssen also ein
Produkt auf zwei verschiedene Weisen in zwei Faktoren zerlegen kšnnen.
Somit Vorgehen: Sei z weder Primzahl noch Quadrat einer Primzahl, also 
. Dann kann z
auf mindestens zwei verschiedene Arten in ein Produkt von zwei verschiedenen
Faktoren zerleget werden, da wir immer auch die ăZerlegungŇ 
zur Verfźgung
haben. Wir kšnnen also schreiben:
Setzen:
Das ist eine Lšsung.
Kontrolle:
Allenfalls kann durch
einen gemeinsamen Teiler dividiert werden.
4
Beispiele
5
Pythagoreische Dreiecke
Was geschieht, wenn z eine Quadratzahl ist? Dann ist 
und 
. Die restlichen Seiten b, c, d bilden ein pythagoreisches Dreieck mit den Katheten b und d
sowie der Hypotenuse c.
Beispiel:
Wir erhalten das
klassische pythagoreische Dreieck.
Weitere Beispiele:
