Hans Walser, [20141016]
Pythagoreische Vierecke mit orthogonalen Diagonalen
1 Worum geht es
Gesucht sind Vierecke mit orthogonalen Diagonalen, bei denen die Seiten und die Diagonalen ganzzahlig sind.
Als Hilfsmittel werden pythagoreische Dreiecke verwendet.
2 Vierecke mit orthogonalen Diagonalen
Ein Viereck mit den Seiten a, b, c, d hat genau dann orthogonale Diagonalen, wenn:
Es verschwindet die alternierende Summe der Quadrate der Seiten.
(Haag, 2003), (Walser, 2013).
3 Ganzzahlige Seiten und Diagonalen
Wir
arbeiten mit zwei primitiven pythagoreischen Zahlentripeln 
und 
. Es ist also 
und 
. Damit bauen wir die Figur der Abbildung 1. Die zum
ersten pythagoreischen Zahlentripel gehšrenden Dreiecke sind gelb, die anderen zyan gezeichnet. Die
pythagoreischen Dreiecke werden auf bŸndige Katheten gezoomt. Die Zoomfaktoren
sind reihum 
.
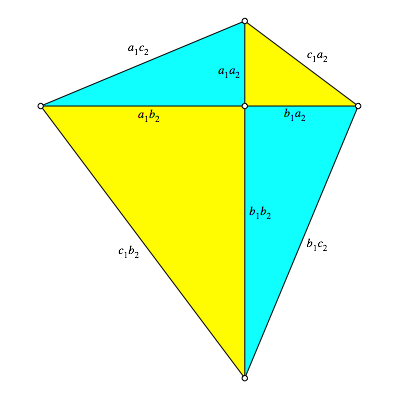
Abb. 1: Viereck aus pythagoreischen Dreiecken
Es sind die Seiten, die Diagonalenabschnitte und damit auch die Diagonalen ganzzahlig.
FŸr den FlŠcheninhalt A des Viereckes erhalten wir:
Da 
gerade
sind, ist der FlŠcheninhalt A
ganzzahlig.
4 Sehnenviereck
Das Viereck ist ein Sehnenviereck (Abb. 2). Dies kann entweder mit WinkelŸberlegungen (Ortsbogen) oder mit dem Satz des PtolemŠus gezeigt werden. FŸr den Umkreisradius r ergibt sich:
Da bei
primitiven pythagoreischen Zahlentripeln die 
ungerade
sind, ist der Umkreisradius r echt halbzahlig.
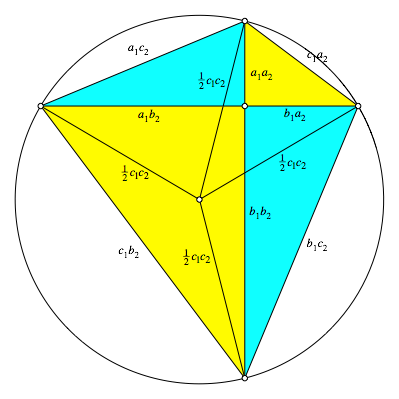
Abb. 2: Sehnenviereck
5 Neue Aufteilung
Mit dem Umkreismittelpunkt kann das Viereck neu sektioniert werden. Dabei entstehen von den beiden Typen der pythagoreischen Dreiecke je vier kongruente Exemplare (Abb. 3).
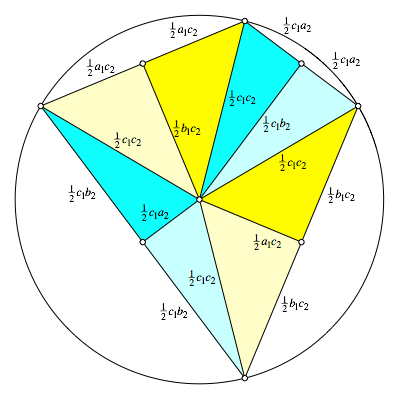
Abb. 3: Aufteilung in kongruente pythagoreische Dreiecke
6 Beispiel
Mit 
und 
ergeben
sich die Werte der Abbildung 4.
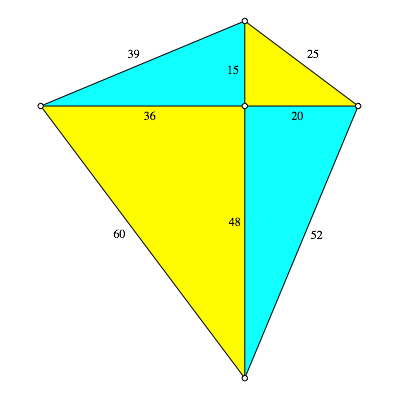
Abb. 4: Beispiel
Die beiden Diagonalen haben die LŠngen e = 56 und f = 63.
Der Umkreisradius ist r = 32.5.
7 Andere ganzzahlige Lšsung?
Mit gegebenen Seiten a = 25, b = 39, c = 60, d = 52 ist das Viereck noch nicht festgelegt. Wir kšnnen noch die eine Diagonale e wŠhlen und dann mit der Heronschen FlŠcehnformel die andere Diagonale ausrechnen. Nachstehend ein brute force Programm fŸr unser Beispiel:
a:= 25: b:=39:
c:=60: d:=52:
for e from
1 to 80 do
q[e]:=1/e/2*sqrt((a+b+e)*(-a+b+e)*(a-b+e)*(a+b-e)):
s[e]:=1/e/2*sqrt((c+d+e)*(-c+d+e)*(c-d+e)*(c+d-e)):
f[e]:=q[e]+s[e]:
if type(f[e],
integer) then print(e,
f[e]) end;
end:
Wir erhalten die beiden FŠlle:
e = 16, f = 63
e = 56, f = 63
Die zweite Lšsung ist unser Beispiel. Die erste Lšsung ist nicht konvex und entsteht aus unserem Beispiel durch Einspiegeln (Abb. 5). Wir haben also keine echt neue Lšsung. Es ist aber kein Sehnenviereck mehr.
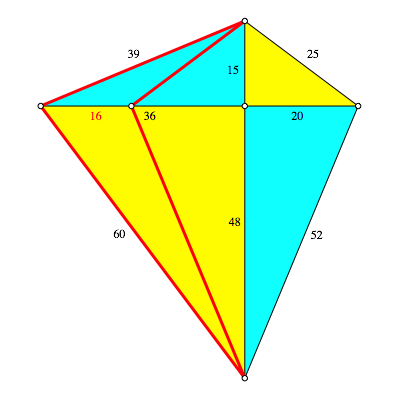
Abb. 5: Die andere Lšsung
Literatur
Haag, Wilfried (2003): Wege zu geometrischen SŠtzen. Stuttgart: Klett. ISBN 3-12-720120-6
Walser, Hans (2013): Vergessene Vierecke. In: Filler, Andreas / Ludwig, Mathias (Hrsg.): Wege zur Begriffsbildung fŸr den Geometrieunterricht. Ziele und Visionen 2020. VortrŠge auf der 29. Herbsttagung des Arbeitskreises Geometrie in der Gesellschaft fŸr Didaktik der Mathematik vom 14. bis 16. September 2012 in SaarbrŸcken. Hildesheim : Franzbecker 2013. ISBN: 978-3-88120-589-4. S. 153-166.