Hans Walser, [20130729b]

Pythagoras mit Dreiecken

1 Worum es geht

Den Seiten eines rechtwinkligen Dreieckes setzen wir regelmäßige Dreiecke auf (Abb. 1) und suchen eine passende Zerlegung für die Flächengleichheit.

Abb. 1: Grau + Orange = Braun

2 Bezeichnungen

Wir bezeichnen die drei Seiten des rechtwinkligen Dreiecks so, dass . Es ist dann .

Bei der Farbgebung wurde versucht, mit möglichst wenigen Farben auszukommen, aber doch die Symmetrien möglichst zu wahren.

3 Allgemeiner Fall

Für den allgemeinen Fall müssen wir unterscheiden zwischen („kleines“ rechtwinkliges Dreieck, Abbildung 2) und („großes“ rechtwinkliges Dreieck, Abbildung 3). Den Übergangsfall behandeln wir unter den Sonderfällen.

3.1 Kleines rechtwinkliges Dreieck

Abb. 2: Kleines rechtwinkliges Dreieck

Wir benötigen insgesamt sieben Puzzle-Teile, aber nur drei verschiedene Formen.

An den inneren Grenzpunkten der Puzzle-Teile kommen immer drei Teile (drei Farben) zusammen.

3.2 Großes rechtwinkliges Dreieck

Für wird das Dreieck an der Kathete a zu sperrig. Wir müssen Ecken abschneiden.

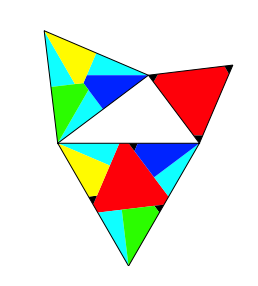
Abb. 3: Großes rechtwinkliges Dreieck

4 Sonderfälle

4.1 Neckischer Fall

Einen neckischen Sonderfall erhalten wir mit (Abb. 4). Es ist dann . Im gleichseitigen Dreieck auf der Hypotenuse c haben wir nur Grenzpunkte, bei denen vier Teile, also auch vier Farben, zusammenkommen.

Abb. 4: Neckischer Sonderfall

Dieser Sonderfall erlaubt eine Variante (Abb. 5).

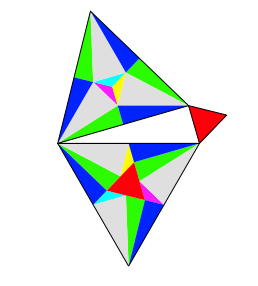
Abb. 5: Variante

4.2 Übergangsfall

Im oben erwähnten Übergangsfall ist (Abb. 6). Das rechtwinklige Dreieck ist ein halbes gleichseitiges Dreieck.

Abb. 6: Übergangsfall

4.3 Halbes DIN-Rechteck

Wir haben ein rechtwinkliges Dreieck mit dem Seitenverhältnis . Zunächst lässt sich das kleinere Kathetendreieck so in das Hypotenusendreieck einpassen, dass die Seiten des Kathetendreiecks orthogonal zu denen des Hypotnusendreiecks werden (Abb. 7).

Abb. 7: Einpassen des Kathetendreiecks

Es bleiben drei Dreiecke mit Winkeln 30°-60°-90° übrig. Dafür muss eine schöne gemeinsame Zerlegung mit dem großen Kathetenquadrat gefunden werden, eine Aufgabe, die sich als nicht so einfach erwies. Die Abbildung 8 zeigt eine symmetrische Lösung.

Abb. 8: Symmetrische Lösung

4.4 Pythagoreische Dreiecke

Bei pythagoreischen Dreiecken gibt es immer die Lösung, alle Dreiecke mit einem regulären Dreiecksraster zu füllen. Die Abbildung 9 zeigt dies am Beispiel des Lehrerdreiecks mit dem Seitenverhältnis . Die Herausforderung besteht nur noch darin, die Farben regelmäßig zu verteilen.

Abb. 9: Pythagoreisches Dreieck

Natürlich können Dreiecke zu größeren Puzzle-Teilen zusammengefasst werden (Abb. 10).

Abb. 10: Größere Puzzle-Teile

Wird auf Symmetrie verzichtet, reichen noch weniger Teile (Abb. 11).

Abb. 11: Ohne Symmetrie

4.5 Gleichschenklig rechtwinkliges Dreieck

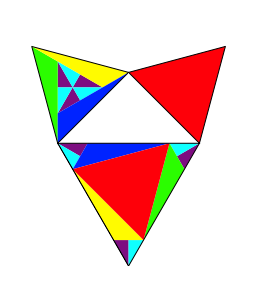
Abb. 12: Rechtwinklig gleichschenkliges Dreieck