Hans Walser, [20150617]
Pythagoras mit Šhnlichen rechtwinkligen Dreiecken
1 Der einfachste Zerlegungsbeweis fŸr den Satz des Pythagoras
Die Abbildung 1 zeigt den einfachsten Zerlegungsbeweis fŸr den Satz des Pythagoras.
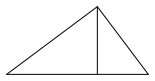
Abb. 1: Einfachster Zerlegungsbeweis fŸr den Satz des Pythagoras
Das Einfachste ist immer das Schwierigste. Daher im Folgenden die ErklŠrung fŸr diesen Zerlegungsbeweis.
2 ErklŠrung
Der Satz des Pythagoras gilt ja nicht nur fŸr an die Seiten angesetzte Quadrate, sondern fŸr beliebige zueinander Šhnliche Figuren mit den Seiten als ReferenzlŠnge. Die Abbildung 2 zeigt ein Beispiel.
Abb. 2: Blau = Rot + GrŸn
Insbesondere kšnnen wir das ursprŸngliche rechtwinklige Dreieck als Form fŸr die angesetzten Šhnlichen Figuren verwenden (Abb. 3). Aus Šsthetischen GrŸnden haben das rote und das grŸne Dreieck gegenŸber dem ursprŸnglichen Dreieck und auch gegenŸber dem blauen Dreieck eine umgekehrte Orientierung.
Abb. 3: Blau = Rot + GrŸn
Die Abbildung 4 zeigt den Zerlegungsbeweis.
Abb. 4: Zerlegungsbeweis
Wenn wir die farbigen Dreiecke der Abbildung 3 je um die Hypotenusenmitte in das ursprŸngliche rechtwinklige Dreieck hineindrehen (Drehung um 180¡), ergibt sich die Figur der Abbildung 1.