Hans Walser, [20111226b]

Pythagoras im Dreiecksraster

Es wird die Idee der pythagoreischen Dreiecke mit dem regulären Dreiecksraster kombiniert.

1 Beispiele

Bei den folgenden Beispielen ist jeweils die „Schlüsselrechnung“ angegeben.

Die Abbildung 1 zeigt die Minimallösung. Leider müssen wir an den Ecken des Hypotenusendreiecks mit zusammengestückelten Dreiecken arbeiten.

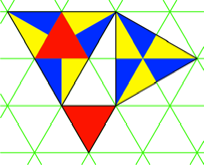
Abb. 1: Schlüsselrechnung:

Durch Halbieren der Maschenweite können wir im Hypotenusendreieck mit ganzen Rasterdreiecken arbeiten (Abb. 2).

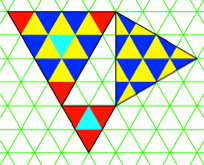
Abb. 2: Schlüsselrechnung:

In der Abbildung 3 sind nur noch die Ecken des Hypotenusendreiecks im Raster. Die „Zähldreiecke“ sind aber kongruent zu den Rasterdreiecken und stimmen anzahl- und flächenmäßig mit den Zähldreiecken in den beiden Kathetendreiecken überein.

Wir haben eine kleine Parkett-Unschönheit an den Ecken des Hypotenusendreieckes. Wir dürfen aber die drei gelben Eckdreiecke nicht durch blaue ersetzen, weil sonst die Anzahlen der gelben und blauen Dreiecke nicht mit den entsprechenden Anzahlen im Kathetendreieck übereinstimmen. Nachzählen erlaubt.

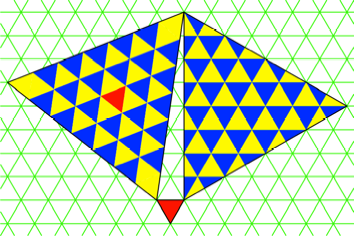
Abb. 3: Schlüsselrechnung:

Im Beispiel der Abbildung 4 geht alles schön auf.

Abb. 4: Schlüsselrechnung:

Noch zwei weitere Beispiele. Wer findet weitere Beispiele?

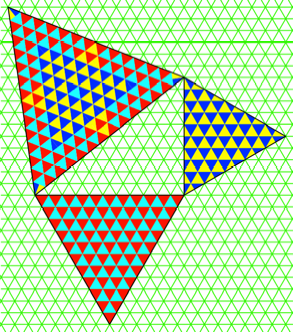
Abb. 5: Schlüsselrechnung:

Abb. 6: Schlüsselrechnung:

2 Überlagerungsraster

Wir nehmen in der Abbildung 6 den Hintergrundraster in den Vordergrund (Abb. 7).

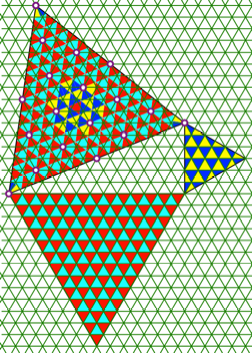
Abb. 7: Raster im Vordergrund. Überlagerung

Es gibt nun Rasterpunkte des ursprünglichen Dreiecksrasters, welche mit Rasterpunkten des Hypotenusendreiecksrasters übereinstimmen. Diese Rasterpunkte bilden ihrerseits ein Dreiecksraster (Abb. 8).

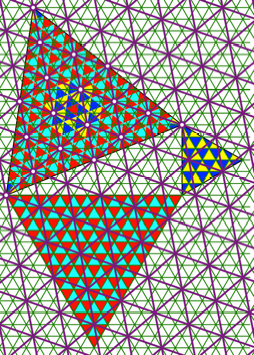
Abb. 8: Überlagerungsraster

Der Überlagerungsraster sitzt symmetrisch über dem ursprünglichen Dreiecksraster und dem Raster des Hypotenusendreieckes. An der linken unteren Ecke des rechtwinkligen Dreieckes sehen wir, das eine der drei Rasterlinien des Überlagerungsrasters die äußere Winkelhalbierende ist.

3 Hintergrund

Unsere „Schlüsselgleichungen“ waren von der Form . Allgemein finden wir Beispiele über die Lösungen der diophantischen Gleichung.

Die Tabelle 1 zeigt die ersten Lösungen. Dabei wurden nur teilerfremde Lösungen aufgenommen. So fehlt zum Beispiel der Fall der Abbildung 2.

p	q	r
1	1	2
1	4	7
1	15	26
1	56	97
11	4	13
11	5	14
11	21	38
11	24	43
11	80	139
11	91	158
13	3	14
13	8	19
13	20	37
13	35	62
13	77	134
13	132	229
23	7	26
23	12	31
23	40	73
23	55	98
23	153	266
37	5	38
37	28	61
37	48	91
37	117	206
37	187	326
47	8	49
47	33	74
47	65	122
47	140	247
59	11	62
59	40	91
59	84	157
59	171	302

Tabelle 1: Erste Lösungen

Die Vermutung, dass p eine Primzahl sein muss, ist aber falsch. Die Tabelle 2 zeigt die ersten Lösungen, bei denen p keine Primzahl ist.

p	q	r
1	1	2
1	4	7
1	15	26
1	56	97
121	9	122
121	104	217
121	140	271
143	17	146
143	28	151
143	95	218
143	112	241
143	180	343
169	55	194
169	84	223

Tabelle 2: Erste Lösungen mit nicht primem p

4 Frage des mittleren Dreieckes

Beim Verteilen der Zähldreiecke auf das Hypotenusendreiecks möchte man natürlich möglichst eine Anordnung mit hoher Symmetrie, im Idealfall mit der Symmetrie des gleichseitigen Dreiecks. Dazu ist es wichtig, zu Beginn abzuklären, ob es in der Mitte ein Dreieck hat. Da hilft folgende Einsicht (Abb. 9).

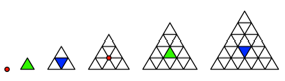
Abb. 9: Was ist in der Mitte?

Mit der Seitenlänge n der Dreiecke gilt:

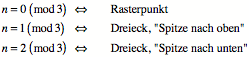
Das kann induktiv bewiesen werden.

5 Link mit pythagoreischen Dreiecken

Ein jedermann im Lande kennt die Abbildung 10.

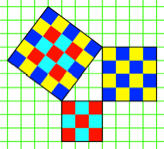
Abb. 10: Pythagoreisches Dreieck

Natürlich können die Zählquadrate durch Zähldreiecke ersetzt werden (Abb. 11). Dabei werden allerdings in den beiden Kathetenfiguren die Binnenverteilungen der Zählfiguren verändert. Statt zum Beispiel fünf rote und vier cayn haben wir sechs rote und drei cyan. Die Gesamtsumme bleibt sich aber gleich.

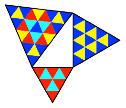
Abb. 11: Dasselbe mit Dreiecken

Leider passen nicht einmal die beiden Kathetendreiecke in denselben Raster. Die Dreiecke sind unterschiedlich orientiert.