Hans Walser, [20160425]

Pythagoras-Schmetterling

1 Das Phänomen

Wir beginnen mit einem beliebigen rechtwinkligen Dreieck und zeichnen die übliche Pythagoras-Figur. Dann fügen wir zwei weitere Quadrate an (rot in Abbildung 1).

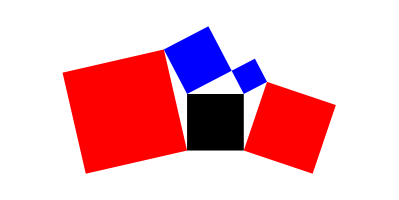
Abb. 1: Noch zwei Quadrate

In der Schule lernen wir den Satz des Pythagoras: Die Flächensumme der beiden blauen Quadrate ist gleich der Fläche des schwarzen Quadrates:

blau = schwarz (1)

Beim Spielen mit einer dynamischen Geometrie-Software stellen wir fest, dass die Flächensumme der beiden roten Quadrate das Fünffache der Fläche des schwarzen Quadrates ist, und das unabhängig von der Form des rechtwinkligen Dreieckes:

rot = fünf mal schwarz (2)

Da ist kein Halten mehr. In der Abbildung 2 sind zwei weitere Schritte eingezeichnet.

Abb. 2: Pythagoras-Schmetterling

Wir stellen fest:

hellblau = zehn mal schwarz (3)

und:

gold = 29 mal schwarz (4)

Die Bezeichnung Schmetterling bezieht sich auf die Struktur der Figur, welche links und rechts die gleiche ist. Ein realer Schmetterling ist auch größenmäßig links und rechts einigermaßen gleich (Abb. 3, vgl. (Walser 2014)).

Abb. 3: Distelfalter

Als Mathematiker frägt man nach dem Beweis. Als normaler Mensch möchte man wissen, wie es weiter geht.

Beides lässt sich mithilfe des Max-und-Moritz-Theorems (Busch 1865) angehen.

2 Das Max-und-Moritz-Theorem

Wir beginnen mit zwei Quadraten (blau in Abb. 4), die an einer Ecke gelenkig verbunden sind. Dann fügen wir zwei weitere Quadrate an (rot in Abb. 4).

In dieser Situation gilt das Max-und-Moritz-Theorem:

rot = zwei mal blau (5)

Abb. 4: rot = zwei mal blau

Für den Beweis arbeiten wir mit den Bezeichnungen der Abbildung 5.

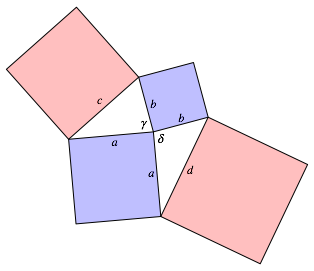
Abb. 5: Bezeichnungen

Die Winkel und ergänzen sich auf 180°. Daher ist:

(6)

Aus dem Kosinus-Satz ergibt sich:

(7)

Wegen (6) ergibt sich durch Addition der beiden Zeilen von (7):

(8)

Damit ist das Max-und-Moritz-Theorem bewiesen.

Nun zurück zum Pythagoras-Schmetterling.

3 Beweis der Phänomene

Wir arbeiten mit den Bezeichnungen der Abbildung 6.

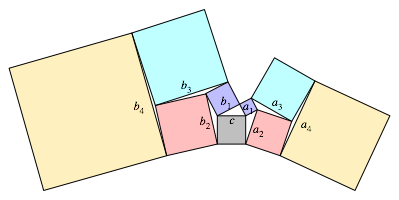
Abb. 6: Beweisfigur

Zunächst ist:

(9)

In der Abbildung 6 sind das schwarze und dass kleine blaue Quadrat in der Position der beiden blauen Quadrate der Abbildung 5, das große blaue und das kleine rote Quadrat in der Position der beiden roten Quadrate. Nach dem Max-und-Moritz-Theorem gilt:

(10)

Und analog:

(11)

Addition der beiden Zeilen (10) und (11) ergibt wegen (9):

(12)

Das ist die Aussage (2).

Weiter ist rechts:

(13)

Analog links:

(14)

Addition der Zeilen (13) und (14) ergibt wegen (9) und (12):

(15)

Das ist die Aussage (3).

Weiter gilt rechts:

(16)

Analog gilt auf der linken Seite:

(17)

Addition der Zeilen (13) und (14) ergibt wegen (9), (12) und (15):

(18)

Das ist die Aussage (4).

4 Wie geht es weiter?

Der nächste Schritt sieht so aus:

(19)

Addition:

(20)

Und aus Spaß an der Freude noch ein Schritt:

(21)

Addition:

(22)

5 Die Schmetterlings-Folge

Die Flächensummen sind Vielfache der Fläche des schwarzen Quadrates. Wir schreiben:

(23)

Gesucht ist die Schmetterlings-Folge . Wir wissen bereits:

n	1	2	3	4	5	6
	1	5	10	29	73	194

Tab. 1: Schmetterlings-Folge

Allgemein ist (für , für kleinere n müssen die Bezeichnungen geändert werden):

(24)

Addition unter Verwendung der Schreibweise (23):

(25)

Daraus ergibt sich die Rekursion:

(26)

Mit den Startwerten aus der Tabelle 1 ergeben sich die Werte der Tabelle 2(vgl. [1]). Für die Quotientenfolge zweier aufeinanderfolgender Folgenglieder zeichnet sich ein bekannter Grenzwert ab (Quadrat des Goldenen Schnittes, vgl. (Walser 2013)).

n			n
1	1	5	11	23761	2.618155802
2	5	2	12	62210	2.617987462
3	10	2.900000000	13	162865	2.618051761
4	29	2.517241379	14	426389	2.618027201
5	73	2.657534247	15	1116298	2.618036582
6	194	2.603092784	16	2922509	2.618032998
7	505	2.623762376	17	7651225	2.618034367
8	1325	2.615849057	18	20031170	2.618033844
9	3466	2.618869013	19	52442281	2.618034044
10	9077	2.617715104	20	137295677	2.618033968

Tab. 2: Schmetterlings-Folge

Bemerkung: Die Rekursionsformel (26) ist symmetrisch. Wenn wir rückwärts rechnen, erhalten wir:

(27)

Die Tabelle 3 zeigt die Werte für negative n. Die Schmetterlings-Folge ist symmetrisch. Der Symmetriepunkt ist bei . Man kann sich überlegen, was dieser Symmetriepunkt geometrisch bedeutet.

n		n
—20	137295677	—8	1325
—19	52442281	—7	505
—18	20031170	—6	194
—17	7651225	—5	73
—16	2922509	—4	29
—15	1116298	—3	10
—14	426389	—2	5
—13	162865	—1	1
—12	62210	0	2
—11	23761	1	1
—10	9077	2	5
—9	3466	3	10

Tab. 3: Negative Indizes

6 Grenzfall. Fibonacci

Wir lassen nun die eine Kathete des Ausgangsdreieckes gegen null gehen: . Aus der Abbildung 6 sehen wir, dass dann die Figur die Grenzlage der Abbildung 7 einnimmt.

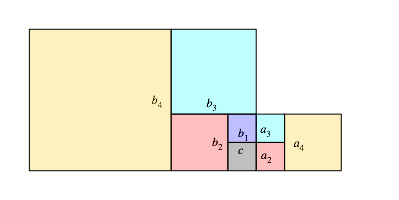
Abb. 7: Grenzlage

Wir erkennen in dieser Grenzlage zweimal die Fibonacci-Packung der Quadrate mit den Seitenlängen der Fibonacci-Folge. Die Abbildung 8 zeigt dasselbe etwas ausführlicher.

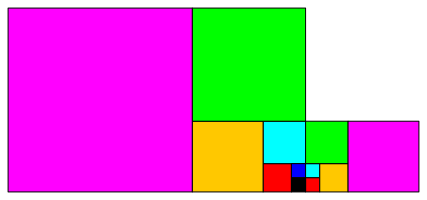
Abb. 8: Fibonacci-Packungen

Zur Erinnerung die Fibonacci-Folge (Walser 2012, S. 9, Walser 2013, S. 105):

n	0	1	2	3	4	5	6	7	8
	0	1	1	2	3	5	8	13	21

Für die Seitenlängen der Quadrate gilt in unserem Grenzfall:

Somit ist in unserem Grenzfall:

(28)

Wegen der Invarianz der Flächensumme der Quadrate mit gleichem Index gilt das aber nicht nur im Grenzfall, sondern allgemein.

Vergleich mit (23) ergibt:

(29)

Die Abbildung 9 ist eine schematische Darstellung von (29).

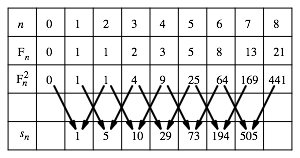
Abb. 9: Schematische Darstellung

7 Explizite Formel

Für die Fibonacci-Zahlen gibt es die explizite Formel von Binet (Walser 2012, S. 13., Walser 2013, S. 106). Diese Formel enthält den Goldenen Schnitt:

(30)

Damit lautet die Formel von Binet:

(31)

Wir setzen (31) in (29) und erhalten:

(32)

Die Folge ist eine Linearkombination dreier geometrischer Folgen. Wegen ist die Folge im Wesentlichen exponentiell wachsend. Für die Quotientenfolge gilt:

(33)

8 Heuristisches Vorgehen

Die explizite Formel können wir direkt aus der Rekursion (26) ohne den Umweg über die Fibonacci-Zahlen gewinnen. Das geht wie folgt.

Wir nehmen einmal heuristisch an, die Quotientenfolge habe einen Grenzwert :

(34)

Aus der Rekursion (26) erhalten wir:

(35)

Daraus ergibt sich durch Grenzübergang :

(36)

Diese kubische Gleichung hat offensichtlich eine erste Lösung . Wir dividieren durch den entsprechenden Linearfaktor:

(37)

Die nun noch quadratische Gleichung

(38)

hat die beiden Lösungen:

(39)

Der Goldene Schnitt tritt halt wieder auf. Nun machen wir für die explizite Formel den Ansatz:

(40)

Einsetzen der Startwerte aus der Tabelle 1 liefert ein Gleichungssystem für .

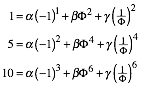(41)

Dieses Gleichungssystem (41) hat die Lösung:

(42)

Einsetzen in den Ansatz (40) ergibt die explizite Formel (32). Diese muss noch induktiv verifiziert werden:

(43)

9 Grafen

Die Abbildung 10 zeigt die Punkte .

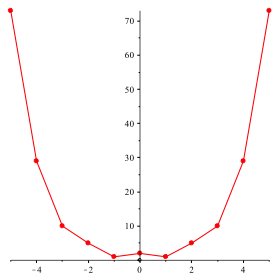
Abb. 10: Punktgraf

Die Punkte sind linear verbunden. Wir sehen die Symmetrie und ahnen das exponentielle Wachstum.

Der Polygonzug der Abbildung 10 zeigt allerdings nicht eine Approximation des Funktionsgrafen von:

(44)

Wegen der Basis in der Mitte hat die Funktion komplexe Funktionswerte. So ist zum Beispiel:

(45)

Die Abbildung 11 zeigt die Kurve mit der Parameterdarstellung:

(46)

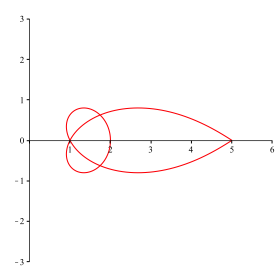
Abb. 11: In der Gaußschen Zahlenebene

Die Abbildung 12 zeigt den Ausschnitt für in überhöhter Darstellung.

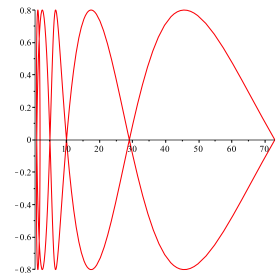
Abb. 12: Größerer Ausschnitt

Literatur

Busch, Wilhelm (1865): Max und Moritz eine Bubengeschichte in sieben Streichen. München: Verlag von Braun und Schneider.

Walser, Hans (2012): Fibonacci. Zahlen und Figuren. Leipzig, EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-60-8.

Walser, Hans (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wußing über populärwissenschaftliche Mathematikliteratur aus Leipzig. Edition am Gutenbergplatz, Leipzig. ISBN 978-3-937219-85-1.

Walser, Hans (2014): Symmetrie in Raum und Zeit. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-46-2.

Weblinks

[1] https://oeis.org/A069921