Hans Walser, [20120529a], [20191026]
Pythagoras-Schwerpunkte
Anregung: Fred Vo§: Die Waage des Pythagoras
1 Worum es geht
Die Pythagoras-Figur ist wohlbekannt.

Abb. 1: Pythagoras-Figur
Wir berechnen Schwerpunkte dieser Figur und Teilen davon, und zwar Eckenschwerpunkte und Flchenschwerpunkte. Au§er bei einem Dreieck sind nmlich Eckenschwerpunkt und Flchenschwerpunkt in der Regel verschieden.
Wir arbeiten mit den Bezeichnungen und der Disposition der Abbildung 2.
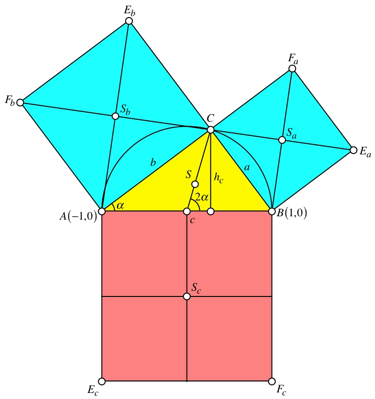
Abb. 2: Bezeichnungen und Disposition
Es ist dann:
![]()
Weiter
seien S der Schwerpunkt des
rechtwinkligen Dreieckes ABC und ![]() die Schwerpunkte
der angesetzten Quadrate. Mit einiger Rechnung finden wir:
die Schwerpunkte
der angesetzten Quadrate. Mit einiger Rechnung finden wir:
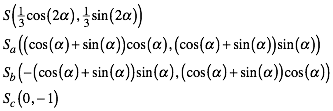
Fr die Au§enecken der angesetzten Quadrate ergibt sich:
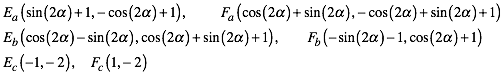
2 Eckenschwerpunkte
Wir haben
bereits ![]() als Schwerpunkt
des Dreiecks ABC.
als Schwerpunkt
des Dreiecks ABC.
Fr den
Schwerpunkt der drei Au§enecken ![]() finden wir aber
ebenfalls
finden wir aber
ebenfalls ![]() , und dasselbe gilt fr die drei Au§enecken
, und dasselbe gilt fr die drei Au§enecken ![]() . Schlie§lich haben auch die drei Punkte
. Schlie§lich haben auch die drei Punkte ![]() diesen
Schwerpunkt.
diesen
Schwerpunkt.
Die vier
Dreiecke ABC, ![]() ,
, ![]() und
und ![]() haben alle
denselben Schwerpunkt S.
haben alle
denselben Schwerpunkt S.
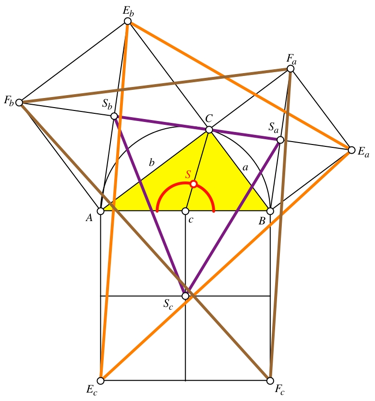
Abb. 3: Gemeinsame Eckenschwerpunkte
Damit haben auch die neun Ecken der Pythagoras-Figur diesen Schwerpunkt S.
Wenn sich der Punkt C auf dem Thaleskreis bewegt, beschreibt der Punkt S einen dazu konzentrischen Kreis mit einem Drittelradius.
3 Flchenschwerpunkte
Das Dreieck ABC hat den Punkt S auch als Flchenschwerpunkt, da im Dreieck Eckenschwerpunkt und Flchenschwerpunkt bereinstimmen.
Im weiteren verwenden wir folgende Bezeichnungen:
T sei der Flchenschwerpunkt der beiden Kathetenquadrate als Gesamtfigur.
U sei der Flchenschwerpunkt der drei Quadrate der Pythagorasfigur.
V schlie§lich sei der Flchenschwerpunkt der gesamten Pythagorasfigur, also Dreieck mit den drei Quadraten.
3.1 Flchenschwerpunkt der beiden Kathetenquadrate
Der
gesuchte Punkt T teilt die Strecke ![]() im Verhltnis
im Verhltnis ![]() , wobei der dem Wert
, wobei der dem Wert ![]() entsprechende
Abschnitt bei
entsprechende
Abschnitt bei ![]() beginnt.
beginnt.
Nun teilt
der Fu§punkt D der Hhe ![]() die Hypotenuse AB im Verhltnis
die Hypotenuse AB im Verhltnis ![]() , wobei der dem Wert
, wobei der dem Wert ![]() entsprechende
Abschnitt bei
entsprechende
Abschnitt bei ![]() beginnt. Dies
folgt aus den so genannten Kathetenstzen, die wir hier zur Seltenheit wieder
einmal brauchen knnen.
beginnt. Dies
folgt aus den so genannten Kathetenstzen, die wir hier zur Seltenheit wieder
einmal brauchen knnen.
Damit lsst sich der Punkt T gem§ Abbildung 4 konstruieren.
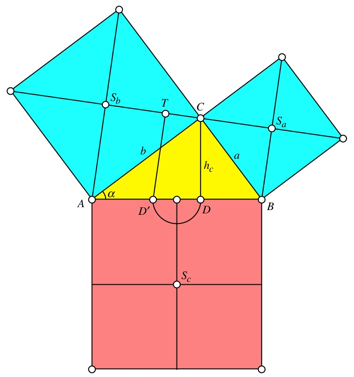
Abb. 4: Konstruktion des Flchenschwerpunktes der Kathetenquadrate
Rechnerisch finden wir:
![]()
Damit
knnen wir die Bahnkurve von T
plotten, wenn C die obere Hlfte des
Thaleskreises durchluft, also fr ![]() (Abb. 5).
(Abb. 5).
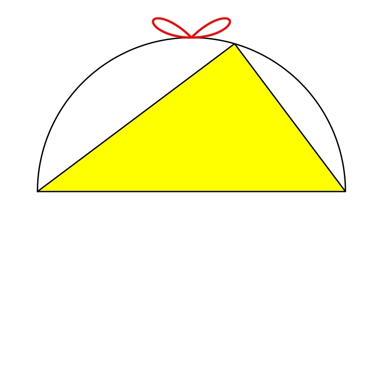
Abb. 5: Bahnkurve des Flchenschwerpunktes der Kathetenquadrate
Fr ![]() durchluft C den gesamten Thaleskreis. Im unteren
Teil sind dann allerdings die Kathetenquadrate aus Orientierungsgrnden nach
innen zu zeichnen. Fr den Punkt T
erhalten wir die Bahnkurve der Abbildung 6.
durchluft C den gesamten Thaleskreis. Im unteren
Teil sind dann allerdings die Kathetenquadrate aus Orientierungsgrnden nach
innen zu zeichnen. Fr den Punkt T
erhalten wir die Bahnkurve der Abbildung 6.
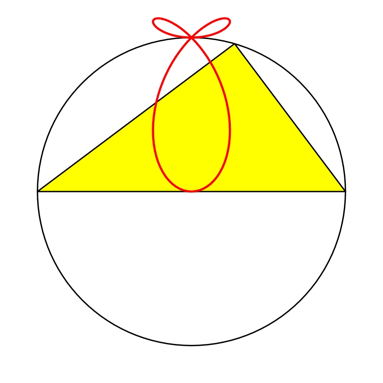
Abb. 6: Verlngerte Bahnkurve
Man kann
nachrechnen, dass sich im Tripelpunkt die Kurven unter Winkeln von 90¡ und 45¡
schneiden: Aus ![]() ergibt sich die
Vektordarstellung:
ergibt sich die
Vektordarstellung:
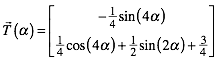
Fr ![]() erhalten wir
erhalten wir ![]() , also den Tripelpunkt. Weiter ist:
, also den Tripelpunkt. Weiter ist:
![]()
Somit haben wir im Tripelpunkt die Tangentialvektoren:
![]()
Daraus ergeben sich die Schnittwinkel von 90¡ und 45¡.
3.2 Flchenschwerpunkt der drei Quadrate
Nun
nehmen wir noch das Hypotenusenquadrat dazu, welches den Schwerpunkt ![]() hat. Da das
Hypotenusenquadrat dasselbe ãGewichtÒ hat wie die beiden Kathetenquadrate
zusammen (das ist ja die Aussage des Satzes von Pythagoras), knnen wir einfach
den Mittelpunkt von T und
hat. Da das
Hypotenusenquadrat dasselbe ãGewichtÒ hat wie die beiden Kathetenquadrate
zusammen (das ist ja die Aussage des Satzes von Pythagoras), knnen wir einfach
den Mittelpunkt von T und ![]() whlen. Fr den
Schwerpunkt U der drei Quadrate
erhalten wir daher:
whlen. Fr den
Schwerpunkt U der drei Quadrate
erhalten wir daher:
![]()
Fr ![]() erhalten wir die
Bahnkurve der Abbildung 7.
erhalten wir die
Bahnkurve der Abbildung 7.
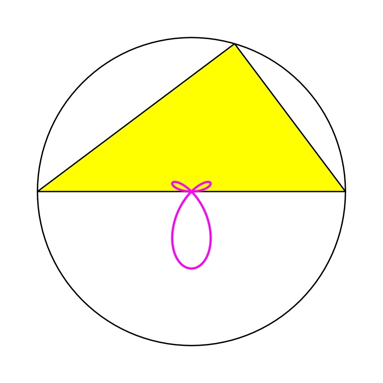
Abb. 7: Bahnkurve des Flchenschwerpunktes der drei Quadrate
3.3 Flchenschwerpunkt der Pythagoras-Figur
Fr den
Flchenschwerpunkt V der Gesamtfigur
mssen wir U und S mit den zugehrigen Flchen, also ![]() und
und ![]() gewichten. Das
lsst sich auch konstruktiv leicht durchfhren. Rechnerisch erhalten wir:
gewichten. Das
lsst sich auch konstruktiv leicht durchfhren. Rechnerisch erhalten wir:
![]()
Die Abbildung 8 zeigt die Bahnkurve.
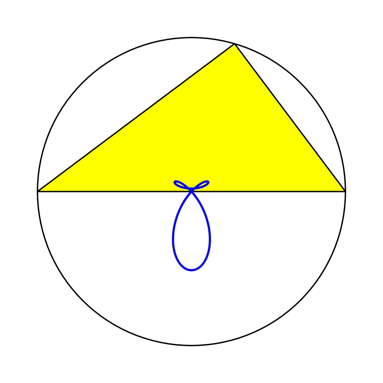
Abb. 8: Bahnkurve des Flchenschwerpunktes der Pythagoras-Figur
Die ist geringfgig anders als die Kurve der Abbildung 7, hat aber keinen Tripelpunkt, sondern drei Doppelpunkte. Die Abbildung 9 zeigt einen Ausschnitt.
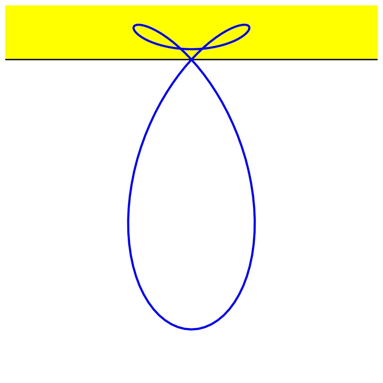
Abb. 9: Ausschnitt
Websites
Fred Vo§: Die Waage des Pythagoras (abgerufen 26.10.2019)
https://www.youtube.com/watch?v=cjKCnEpEEFs