Hans Walser, [20180104], [20210225]
Pythagoras-Zerlegungsbeweise
Anregung: Molokach (2017)
1 Worum geht es?
Zerlegungsbeweise des Satzes von Pythagoras mit Punktsymmetrie.
2 Klassisches Beispiel
Die Abbildung 1 zeigt einen Klassiker (Perigal). Alle drei Quadrate sind punktsymmetrisch unterteilt.

Abb.1: Klassischer Zerlegungsbeweis
Das kleine Kathetenquadrat ist unzerschnitten und gleich orientiert ins Hypotenusenquadrat źbernommen.
3 Duale Version
Die Abbildung 2 zeigt die sozusagen duale Version dazu. Das gro§e Kathetenquadrat ist so gut es geht unzerschnitten und gleich orientiert źbernommen. Das kleine Kathetenquadrat ist genau gleich zerlegt wie das gro§e Kathetenquadrat in der Abbildung 1.

Abb. 2: Duale Version
4 Weiterte Beispiele
Die Abbildungen 3 und 4 zeigen weitere Beispiele. Im Prinzip sind es Vorformen des Beispiels der Abbildung 2.
Im Beispiel der Abbildung 3 sind alle drei Quadrate durch ihre Diagonalen unterteilt. Die Unterteilung der so entstehenden rechtwinklig-gleichschenkligen Dreiecke ist aus (Molokach 2017) źbernommen.
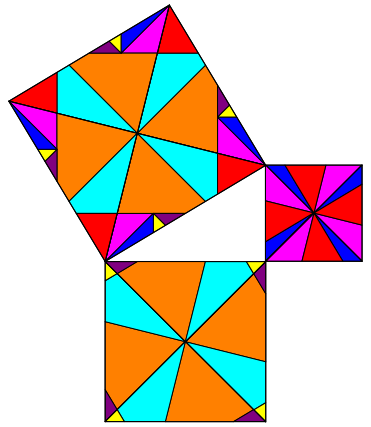
Abb. 3: Beispiel
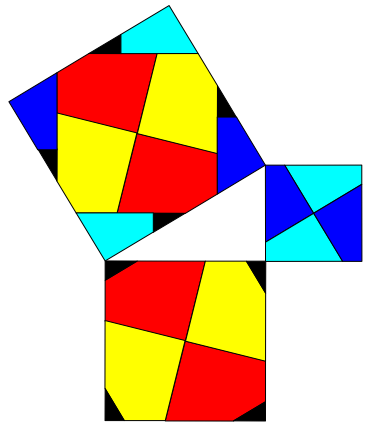
Abb. 4: Beispiel
5 Asymmetrisches Beispiel
Im folgenden Beispiel haben (Abb. 5) wir keine Symmetrien mehr. Die Teile kšnnen nicht mehr translatorisch ineinander źbergefźhrt werden.
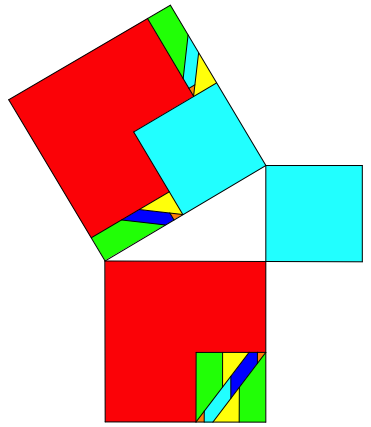
Abb. 5: Asymmetrisches Beispiel
Die Abbildung 6 zeigt die duale Variante.
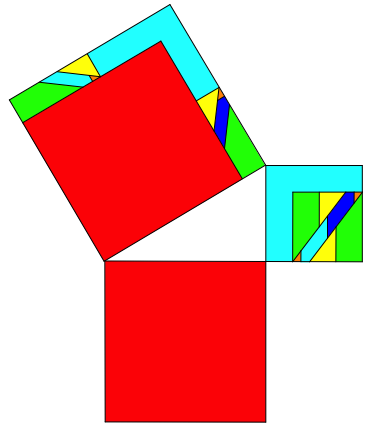
Abb.6: Duale Variante
Literatur
Molokach,
John (2017): Proof Without Words: The Pythagorean Theorem. The College
Mathematics Journal. Vol. 48, No. 5, November 2017, p. 334.