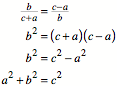Hans Walser, [20111111a]

Ein Beweis des Satzes von Pythagoras

1 Erinnerung

Ein klassischer Beweis des Satzes von Pythagoras basiert auf der Abbildung 1.

Abb. 1: Klassische Beweisfigur

Wir arbeiten mit einem Flächenvergleich:

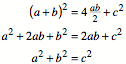
2 Umlegen der Dreiecke

Nun wenden wir zwei der Dreiecke um (die Rückseite ist grün) und setzen zu einem Rechteck zusammen (Abb. 2).

Abb. 2: Umlegen

3 Ähnliche Rechtecke

Wir vermuten, dass das „Loch“ im Innern ein zum Umrissrechteck ähnliches Rechteck ist.

Beweis: Wir zeichnen noch die Diagonalen ein und beschriften gemäß Abbildung 3.

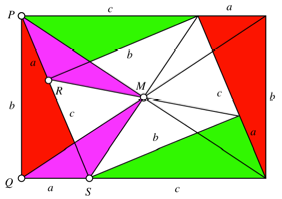
Abb. 3: Bezeichnungen

Die beiden Dreiecke MPR und MQS sind kongruent (gleiche Seiten). Das eine Dreieck ergibt sich aus dem anderen durch eine Drehung um M um den Diagonalenschnittwinkel PMQ des Umrissrechtecks. Damit ist der Diagonalenschnittwinkel RMS des Lochrechtecks gleich groß. Rechtecke mit gleichem Diagonalenschnittwinkel sind ähnlich.

4 Beweis des Satzes von Pythagoras

Das Umrissrechteck hat das Seitenverhältnis , das Lochrechteck das Seitenverhältnis . Aus der Ähnlichkeit der beiden Rechtecke folgt: