Hans Walser, [20201224]
Pythagoras
Anregung und Idee: Rainer Kaenders, Bonn
1 Worum geht es?
Was steckt hinter der Figur (Abb. 1)?
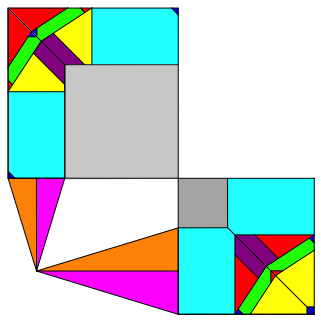
Abb. 1: Was steckt hinter der Figur?
2 Bearbeitung
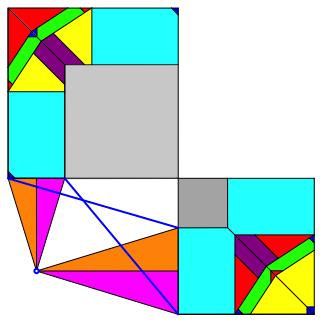
Abb. 2: Verdrehte blaue Strecken
Die beiden blauen Strecken (Abb. 2) sind gleich lang (Drehung um den blauen Punkt).
3 Zwei Pythagoras-Figuren
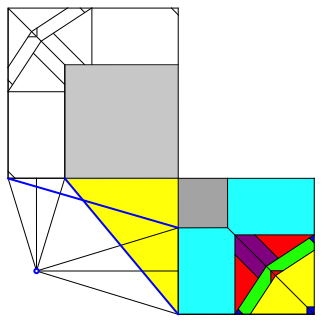
Abb. 3.1: Pythagoras-Figur
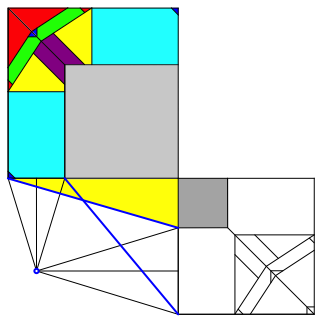
Abb. 3.2: Noch eine Pythagoras-Figur
Die beiden gelben rechtwinkligen Dreiecke haben dieselbe HypotenusenlŠnge.
Die Summe der KathetenflŠchen ist invariant.
4 Auf gemeinsamer Basis
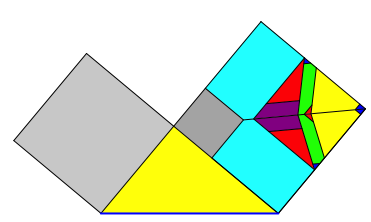
Abb. 4.1: Horizontale Hypotenuse
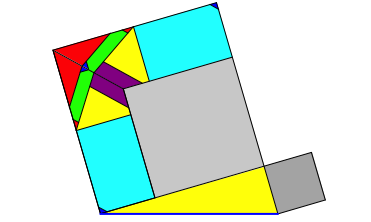
Abb. 4.2: Horizontale Hypotenuse
Invariante KathetenflŠchensumme.
5 Sonderfall
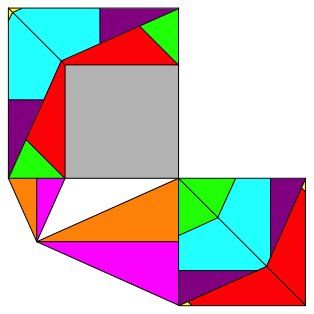
Abb. 5: Worin besteht der Sonderfall?
6 Verdrehte Strecken
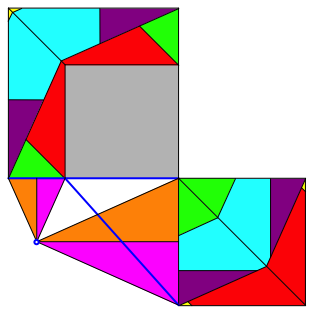
Abb. 6: Verdrehte blaue Strecken
7 Zwei Pythagoras-Figuren?
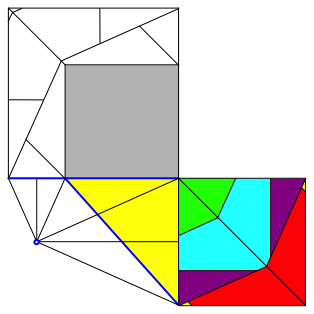
Abb. 7.1: Pythagoras-Figur
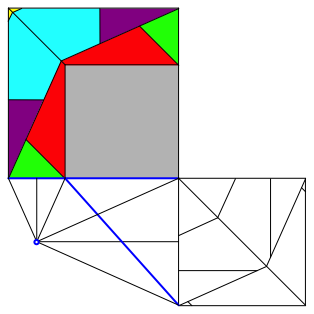
Abb. 7.2: Noch eine Pythagoras-Figur?
8 Auf gemeinsamer Basis
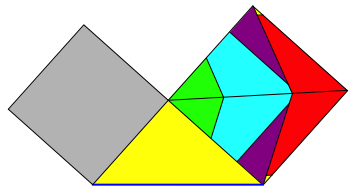
Abb. 8.1: Horizontale Hypotenuse
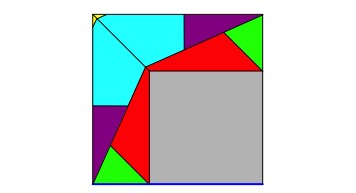
Abb. 8.2: Horizontale Hypotenuse
9 Klassische Darstellung
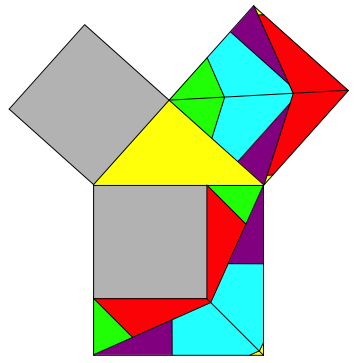
Abb. 9: Zerlegungsbeweis in klassischer Darstellung
Die Zerlegung hat diagonale Achsensymmetrie.