1 Worum geht es?

Bahnkurven in der Pythagoras-Ikone

2 Fragestellung

Gesucht sind die Bahnkurven der Mittelpunkte der Kathetenquadrate, wenn die Ecke C auf dem Thaleskreis bewegt wird (Abb. 1).

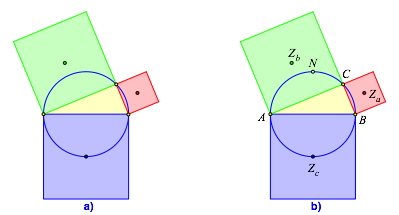
Abb. 1: Mittelpunkte der Kathetenquadrate

3 Bearbeitung

Der Polygonzug BZ_aCZ_bA (Abb. 2a) ist ein halbes Quadrat (Abb. 2b).

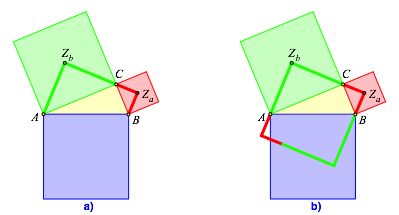
Abb. 2: Quadrat

Wegen der vierteiligen Drehsymmetrie des Quadrates können wir den in Bezug auf das Quadrat schrägen Durchmesser AB um 90° drehen (Abb. 3a). Der oberste Punkt N des Thaleskreises liegt ebenfalls auf dem Rand des Quadrates. Der Mittelpunkt Z_a des Kathetenquadrates über a liegt daher auf dem Thaleskreis über BN (Abb. 3b)

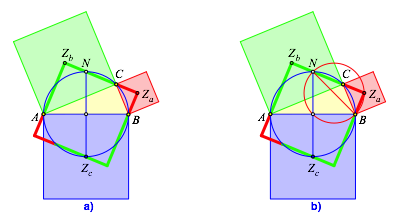
Abb. 3: Symmetrien im Quadrat

Analog für den Mittelpunkt Z_b (Abb. 4a).

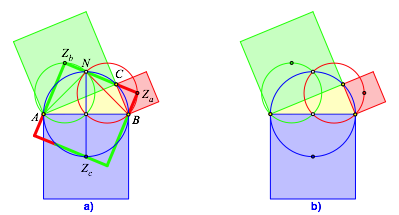
Abb. 4: Die beiden gesuchten Bahnkurven

Die Abbildung 5 illustriert den Sachverhalt.

Abb. 5: Bahnkurven

4 Ausblicke

Die Bahnkurven der Quadratecken sind ebenfalls Kreise (mündliche Mitteilung von Peter Gallin, Bauma) (Abb. 6). Die Kreise passen ins Quadratraster des Hypotenusenquadrates.

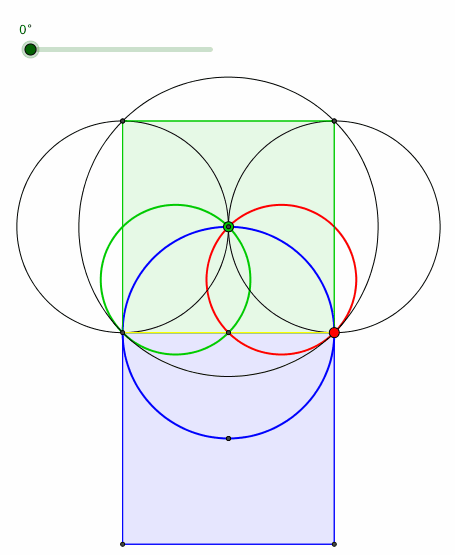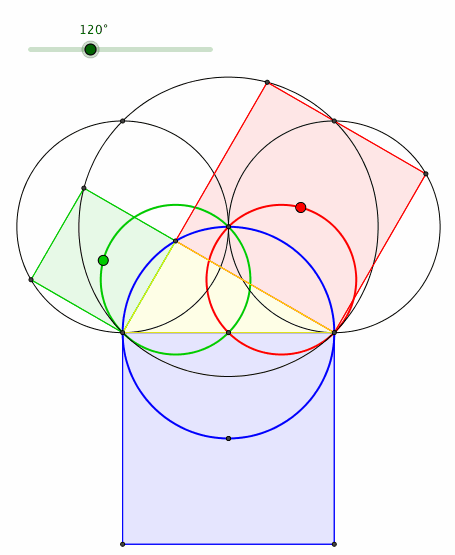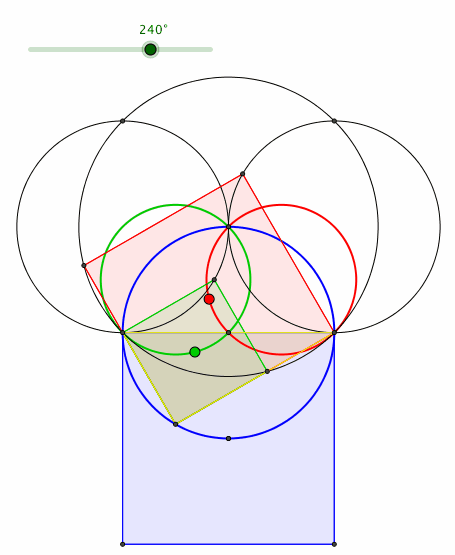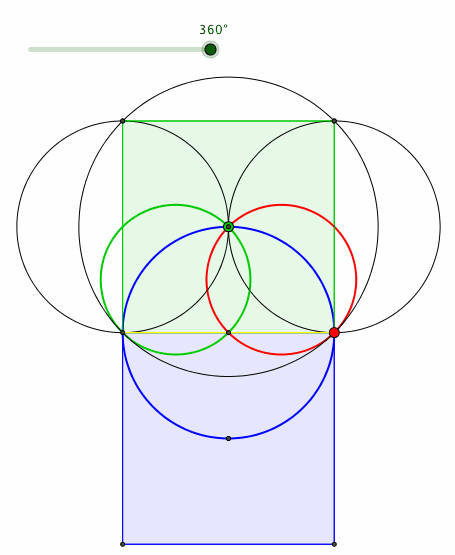
Abb. 6: Quadratecken

Andere Bahnkurven im Kontext des rechtwinkligen Dreiecks.

Websites

Hans Walser: Kardioide
http://www.walser-h-m.ch/hans/Miniaturen/K/Kardioide5/Kardioide5.htm