Hans Walser, [20201127]

Pythagoras in der Kugel

1 Worum geht es?

Visualisierung des Satzes von Pythagoras in der Kugel.

2 Pythagoras mit Kreisen

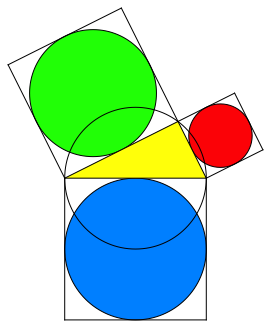
Abb. 1: Pythagoras mit Kreisen

In der Pythagoras-Ikone zeichnen wir die Inkreise der Quadrate (Abb. 1). Nach dem Satz des Pythagoras ist die Flächensumme der beiden Kathetenkreise gleich dem Flächeninhalt des Hypotenusenkreises.

Der Hypotneusenkreis ist gleich groß wie der Thaleskreis des Dreieckes.

3 Im Raum

Nun gehen wir in den Raum. Wir setzen die Kreisscheiben rechtwinklig an die Dreiecksebene an und zwar so, dass jede Dreiecksseite Durchmesser ihres Kreises wird (Abb. 2a). Die Gesamtfigur passt in eine Kugel mit demselben Durchmesser wie der Hypotenusenkreis (Abb. 2b).

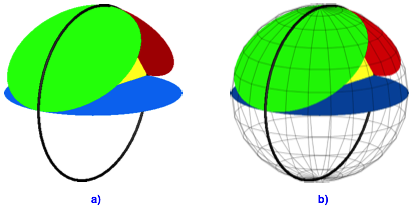
Abb. 2: Pythagoras in der Kugel

4 Animationen

Die folgenden Animationen zeigen die Situation aus verschiedenen Sichten.

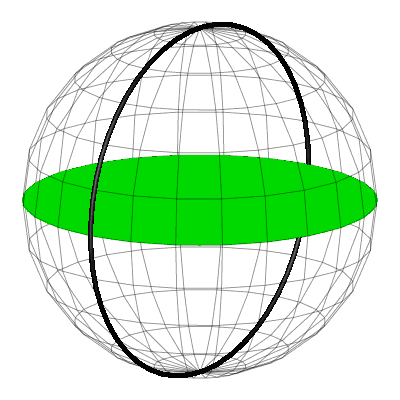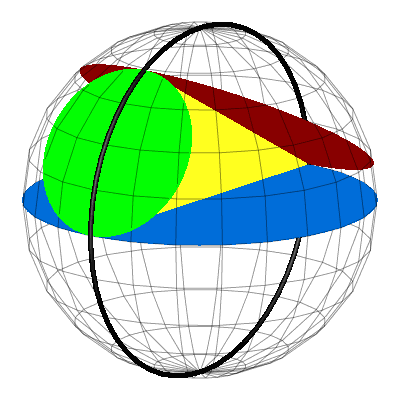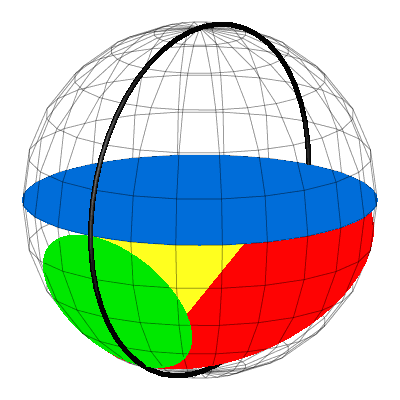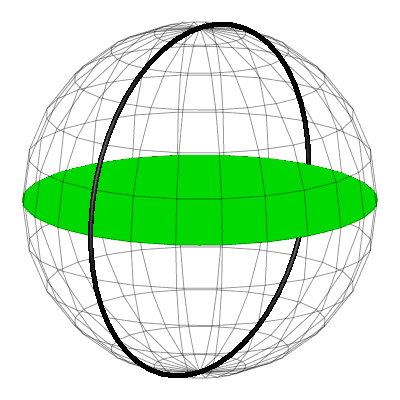
Animation 1: Ansicht

Animation 2: Sicht von vorne

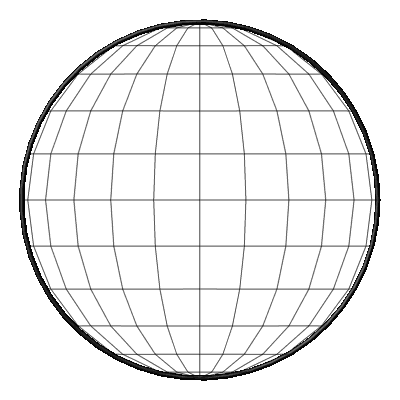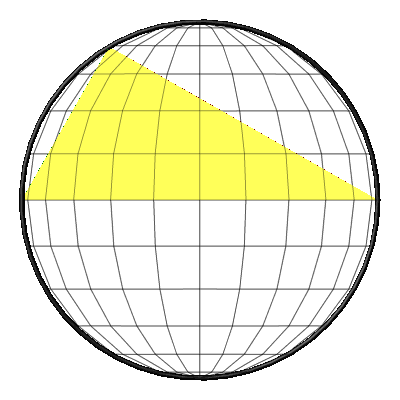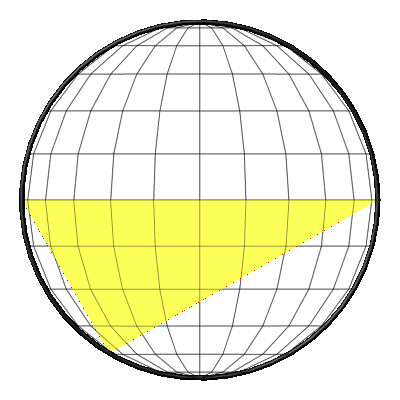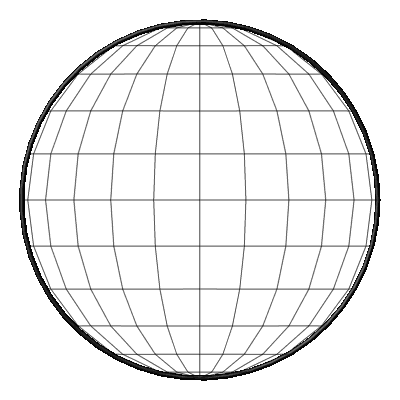
Animation 3: Sicht von der Seite

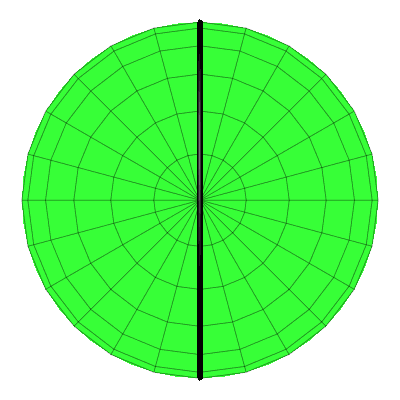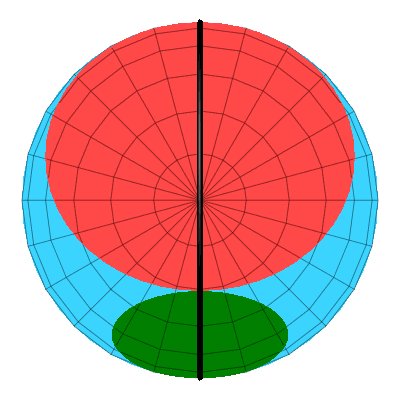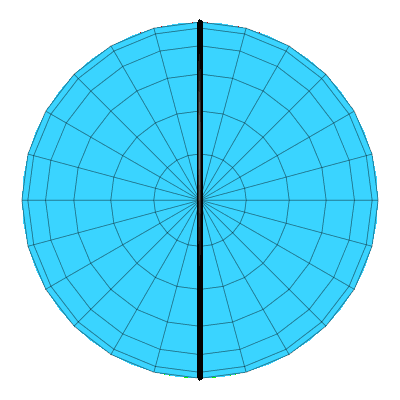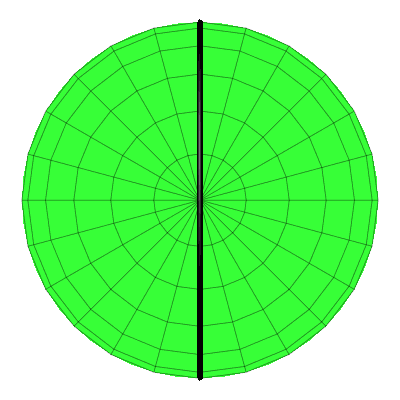
Animation 4: Sicht von oben