Hans Walser, [20160816], [20180420]
Pythagorean Triangles
1 What about?
We give a visualization of the usual parameterization of the Pythagorean triangles.
2 Parameterization of the Pythagorean triangles
Consider integers m > n > 0, m and n relatively prime and with opposite parity.
Set a = m2
– n2, b = 2mn,
c = m2 + n2.
The numbers a, b, and c are a primitive
Pythagorean triple and form a primitive Pythagorean triangle. Any primitive
Pythagorean triple is given by such a pair m
and n (Dickson 1920), (Dickson 1966))
und (Sierpiński 1962).
Table 1 gives the first examples.
|
m |
n |
a |
b |
c |
|
2 |
1 |
3 |
4 |
5 |
|
3 |
2 |
5 |
12 |
13 |
|
4 |
1 |
15 |
8 |
17 |
|
4 |
3 |
7 |
24 |
25 |
|
5 |
2 |
21 |
20 |
29 |
|
5 |
4 |
9 |
40 |
41 |
Tab. 1: Pythagorean triples
3 Visualization
The following figures refer to the cases m = 2, n = 1 (left), and m = 5, n = 2 (right), but the corresponding figures work for any Pythagorean triangle.
We consider not only the Pythagorean triangle itself (yellow), but also the right triangle with legs m and n (red).
Figure 1 gives the basic structure according to (Foster 2016).
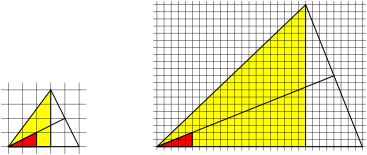
Fig. 1: Pythagorean yellow triangle and red triangle
And now a gallery of pictures. The proofs follow from the definitions of a, b, and c. For incircle and excircles compare (Baptist 1982).
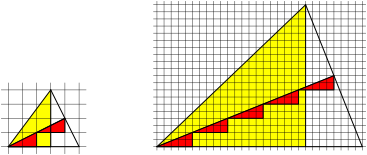
Fig. 2: m red triangles
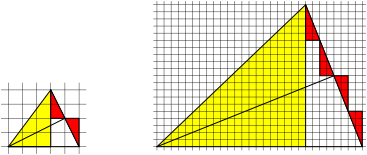
Fig. 3: To times n red triangles
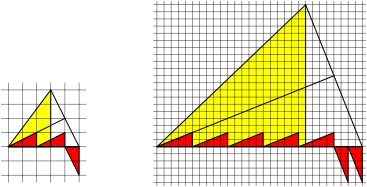
Fig. 4: m red triangles plus n red triangles
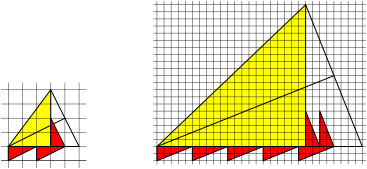
Fig 5: m red triangles minus n red triangles
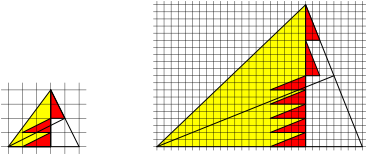
Fig. 6: m red triangles plus n red triangles
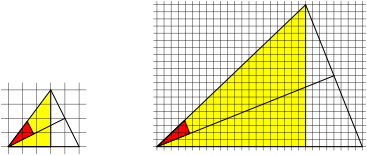
Fig. 7: Rotated red triangle
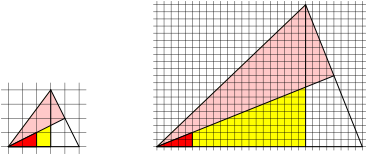
Fig. 8: Rotated and stretched
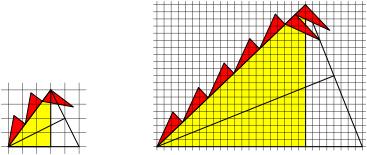
Fig. 9: m rotated plus n rotated red triangles
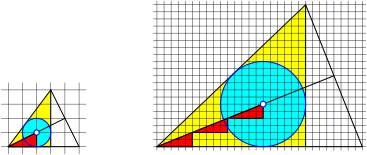
Fig. 10: Incircle: (m – n) red triangles
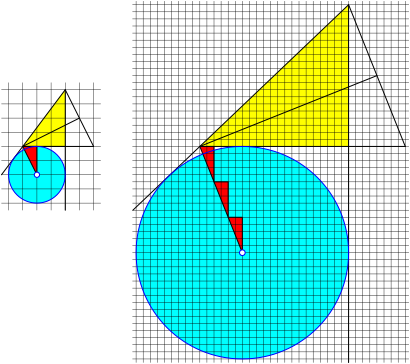
Fig. 11: Excircle: (m – n) red triangles
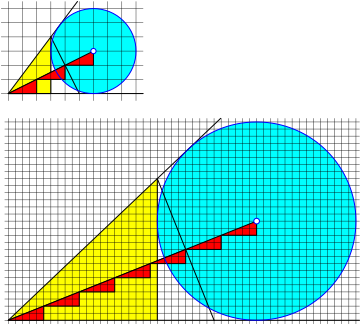
Fig. 12: Excircle: (m + n) red triangles
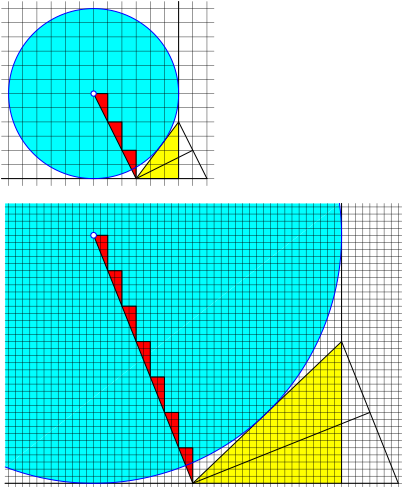
Fig. 13: Excircle: (m + n) red triangles
References
Baptist, Peter (1982): Inkreisradius und pythagoreische Zahlentripel. Praxis der Mathematik, 24, 161-164.
Dickson, Leonard Eugene (1920): History of the Theory of Numbers, II. Diophantine Analysis. Washington: Carnegie Institution.
Dickson, Leonard Eugene (1966): History of the Theory of Numbers; vol II. New York: Chelsea.
Foster, Colin (2016): Proof Without Words: Integer Right Triangle Hypotenuses Without Pythagoras. The College Mathematics Journal. Vol. 47, No. 2, March 2016, 101.
Sierpiński, Wacław (1962): Pythagorean Triangles. Trans. A. Sharma. Yeshiva Univ., New York, 1962. Reprinted by Dover, Minneola, NY, 2003.