1 Worum geht es?

Eckige logarithmische Spiralen im Quadrat mit rationaler Gesamtlänge im Vergleich zur Quadratseite. Geometrische Folgen und Reihen. Pythagoreische Dreiecke

2 Beispiel

Wir legen vier Dreiecke (eines davon gelb) mit dem Seitenverhältnis a:b:c = 3:4:5 in ein Quadrat gemäß Abbildung 1a.

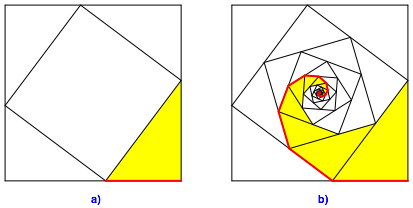
Abb. 1: Dreieck und Spirale

In der Mitte bleibt ein quadratisches Loch. Dieses füllen wir mit einer geeignet verkleinerten und verdrehten Kopie der Startfigur. Iteration des Prozesses führt auf eine Spirale (Abb. 1b).

a) Wie lang ist die rote Spirale im Vergleich zur Quadratseite?

b) Wie groß ist der Flächenanteil der gelben Spirale an der Quadratfläche?

Die rote Kathete in der Abbildung 1a ist der Quadratseite. Die roten Katheten in der Abbildung 1b bilden eine geometrische Folge mit dem Quotienten . Daraus ergibt sich für die Länge s der roten Spirale:

(1)

Das gelbe Dreieck in der Abbildung 1a hat den Anteil der Quadratfläche. Die Flächeninhalte der Dreiecke der Abbildung 1b bilden eine geometrische Folge mit dem Quotienten . Daraus ergibt sich für den Flächeninhalt A der gelben Spirale:

(2)

Das hätten wir allerdings billiger haben können: Wir haben insgesamt vier kongruente Spiralen im Quadrat (Abb. 2).

Abb. 2: Vier Spiralen

Wir hätten mit derselben Startsituation der Abbildung 1a auch andersherum wirtschaften können (Abb. 3). Man beachte, dass das geometrische Grundgerüst (schwarze Linien) in den Abbildungen 1 und 3 übereinstimmt.

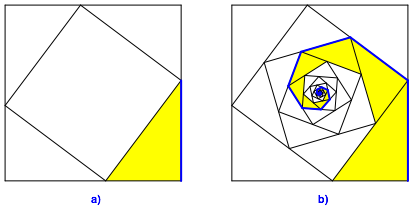
Abb. 3: Zweite Spirale

Für die blaue Spirale erhalten wir analog zu (1) die Länge s = 2 Quadratseiten. Man kann auch direkt überlegen, dass die blaue Kathete der roten misst.

3 Allgemein

Bei einem rechtwinkligen Dreieck mit dem Seitenverhältnis a:b:c erhalten wir für die rote Spirale (gebildet aus den Katheten a) die Länge:

(3)

Für die blaue Spirale (gebildet aus den Katheten b) ergibt sich entsprechend:

(4)

Bei rationalen Katheten sind die Spirallängen wegen der Quadratwurzel für die Hypotenuse in der Regel irrational. Eine Ausnahme bilden wie in unserem Einführungsbeispiel die pythagoreischen Dreiecke.

4 Pythagoreische Dreiecke

Die Tabelle 1 gibt eine Auflistung der ersten pythagoreischen Dreiecke nach der üblichen u,v-Parametrisierung zusammen mit den Spiralenlängen s_a und s_b relativ zur Quadratseite.

In der Spalte von s_b finden wir die ganzzahligen Vielfachen der Quadratseite.

u	v	a	b	c	s_a	s_b
2	1	3	4	5	3/2	2
3	2	5	12	13	5/4	3
4	1	15	8	17	5/2	4/3
4	3	7	24	25	7/6	4
5	2	21	20	29	7/4	5/3
5	4	9	40	41	9/8	5
6	1	35	12	37	7/2	6/5
6	5	11	60	61	11/10	6
7	2	45	28	53	9/4	7/5
7	4	33	56	65	11/8	7/3
7	6	13	84	85	13/12	7
8	1	63	16	65	9/2	8/7
8	3	55	48	73	11/6	8/5
8	5	39	80	89	13/10	8/3
8	7	15	112	113	15/14	8
9	2	77	36	85	11/4	9/7
9	4	65	72	97	13/8	9/5
9	8	17	144	145	17/16	9
10	1	99	20	101	11/2	10/9
10	3	91	60	109	13/6	10/7
10	7	51	140	149	17/14	10/3
10	9	19	180	181	19/18	10
11	2	117	44	125	13/4	11/9
11	4	105	88	137	15/8	11/7
11	6	85	132	157	17/12	11/5
11	8	57	176	185	19/16	11/3
11	10	21	220	221	21/20	11
12	1	143	24	145	13/2	12/11
12	5	119	120	169	17/10	12/7
12	7	95	168	193	19/14	12/5
12	11	23	264	265	23/22	12

Tab. 1: Spiralenlängen

Die Abbildung 4a zeigt das letzte Beispiel der Tabelle (u = 12, v = 11, s_b = 12). Zunächst meinen wir, da sei etwas mit der gelben Spirale schief gelaufen. Das ist aber nur, weil wir die blaue Spirale zunächst nicht so richtig sehen. In der Abbildung 4b diese kräftiger gezeichnet.

Abb. 4: Letztes Beispiel

Websites

Hans Walser: Spiralen im regelmäßigen Vieleck

www.walser-h-m.ch/hans/Miniaturen/S/Spiralen_reg_Vieleck/Spiralen_reg_Vieleck.htm