Hans Walser, [20200804], [20200808]

Pythagoreische Spiralen

1 Worum geht es?

Eckige logarithmische Spiralen im Dreieck und im Sechseck mit rationaler Gesamtlänge im Vergleich zur Seitenlänge. Geometrische Folgen und Reihen. Pythagoreische 60°- und 120°-Dreiecke.

2 Im gleichseitigen Dreieck

2.1 Das klassische Beispiel

Wir legen in jede Ecke ein längenmäßig halb so großes Dreieck (Abb. 1a). Dann iterieren wir den Prozess mit dem in der Mitte übrig bleibenden Dreieck.

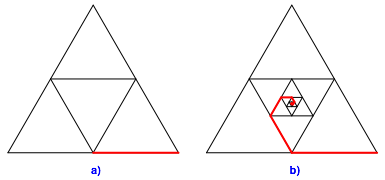
Abb. 1: Kantenmitten

Die rot eingezeichnete eckige logarithmische Spirale ist genau gleich lang wie die Dreiecksseite. Warum?

Natürlich hätten wir die Spirale auch anders herum zeichnen können(Abb. 2).

Abb. 2: Blaue Spirale

2.2 Pythagoreisches 60°-Dreieck

Das Dreieck mit den Seiten a₁ = 3, b = 8 und c = 7 hat den Winkel (Abb. 3a). (Der Index 1 bei a wird nachfolgend erklärt.) Dies kann mit dem Kosinus-Satz verifiziert werden:

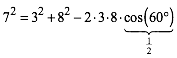(1)

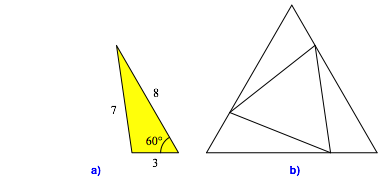
Abb. 3: Pythagoreisches 60°-Dreieck

Dreiecke mit ganzzahligen Seitenlängen und einem Winkel von 60° heißen pythagoreische 60°-Dreiecke.

Wir können drei solche Dreiecke in je eine Ecke eines gleichseitigen Dreiecks platzieren gemäß Abbildung 3b und 4a.

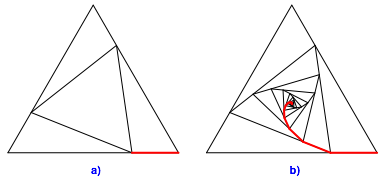
Abb. 4: Pythagoreische Spirale

Die Startstrecke der roten Spirale misst der Dreiecksseite. Die Streckenlängen bilden eine geometrische Folge mit dem Quotienten . Dies ist das Verhältnis der Seitenlängen zweier aufeinanderfolgender Dreiecke. Für die Gesamtlänge der roten Spirale relativ zur Seitenlänge erhalten wir damit:

(2)

Es gibt in der Figur einen weiteren Spiralentyp (Abb. 5).

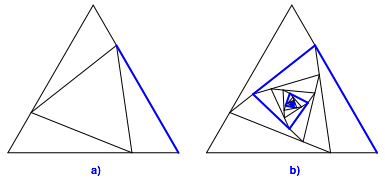
Abb. 5: Blaue Spirale

Die Gesamtlänge der blauen Spirale relativ zur Dreiecksseite ist:

(3)

2.3 Noch ein Beispiel

Das Dreieck mit den Seiten a₂ = 5, b = 8 und c = 7 hat ebenfalls den Winkel (Abb. 6a). Dies kann mit dem Kosinus-Satz verifiziert werden:

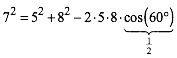(4)

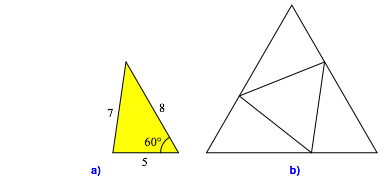
Abb. 6: Pythagoreisches 60°-Dreieck

Interessant ist, dass wir zwei verschiedene Beispiele haben, nämlich a₁ = 3, b = 8, c = 7 und a₂ = 5, b = 8, c = 7, die sich in nur einer Seite unterscheiden und trotzdem je einen Winkel haben. Wenn wir das eine Dreieck spiegeln, ergänzt es sich mit dem anderen zum gleichseitigen Dreieck (Abb. 7).

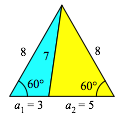
Abb. 7: Ergänzungsdreiecke

Durch Iteration der Abbildung 6b erhalten wir zwei Spiralentypen (Abb. 8).

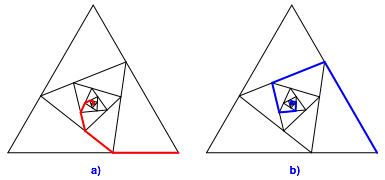
Abb. 8: Spiralen

Für die Gesamtlänge der roten Spirale relativ zur Seitenlänge erhalten wir:

(5)

Für die Gesamtlänge der blauen Spirale relativ zur Seitenlänge entsprechend:

(6)

2.4 Allgemein

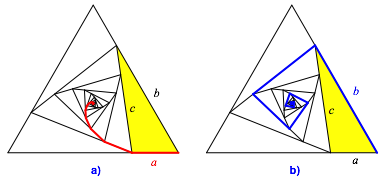
Abb. 9: Allgemein

Mit den Bezeichnungen der Abbildung 9 erhalten wir allgemein für die Spiralenlängen relativ zur Dreiecksseite:

(7)

Bei Verwendung eines pythagoreischen 60°-Dreieckes sind die Spiralenlängen relativ zur Dreiecksseite rational.

Die Tabelle 1 gibt die ersten Beispiele.

u	v	a1	a2	b	c	s1,rot	s1,blau	s2,rot	s2,blau
1	0	1	0	1	1	1	1	–	–
2	1	3	5	8	7	3/4	2	5/6	4/3
3	1	8	7	15	13	4/5	3/2	7/9	5/3
3	2	5	16	21	19	5/7	3	8/9	7/6
4	3	7	33	40	37	7/10	4	11/12	10/9
5	1	24	11	35	31	6/7	5/4	11/15	7/3
5	3	16	39	55	49	8/11	5/2	13/15	11/9
5	4	9	56	65	61	9/13	5	14/15	13/12
6	1	35	13	48	43	7/8	6/5	13/18	8/3
6	5	11	85	96	91	11/16	6	17/18	16/15
7	2	45	32	77	67	9/11	7/5	16/21	11/6
7	3	40	51	91	79	10/13	7/4	17/21	13/9
7	5	24	95	119	109	12/17	7/2	19/21	17/15
7	6	13	120	133	127	13/19	7	20/21	19/18
8	1	63	17	80	73	9/10	8/7	17/24	10/3
8	3	55	57	112	97	11/14	8/5	19/24	14/9
8	7	15	161	176	169	15/22	8	23/24	22/21
9	1	80	19	99	91	10/11	9/8	19/27	11/3
9	2	77	40	117	103	11/13	9/7	20/27	13/6
9	4	65	88	153	133	13/17	9/5	22/27	17/12
9	5	56	115	171	151	14/19	9/4	23/27	19/15
9	7	32	175	207	193	16/23	9/2	25/27	23/21
9	8	17	208	225	217	17/25	9	26/27	25/24
10	3	91	69	160	139	13/16	10/7	23/30	16/9
10	9	19	261	280	271	19/28	10	29/30	28/27

Tab. 1: Beispiele im Dreieck

Offenbar gibt es für jede natürliche Zahl eine passende blaue Spirale.

Die Abbildung 10b zeigt die Spirale, die gleich lang ist wie der Umfang des Dreieckes.

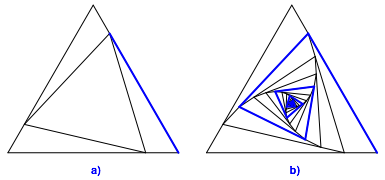
Abb. 10: Spiralenlänge = Dreiecksumfang

3 Im regelmäßigen Sechseck

Wir arbeiten mit pythagoreischen Dreiecken mit dem Winkel . Das einfachste Beispiel hat die Seiten a = 3, b = 5 und c = 7 (Abb. 11).

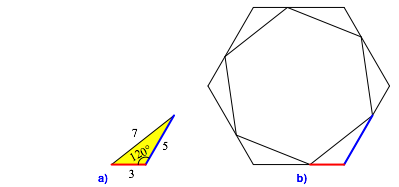
Abb. 11: Pythagoreisches 120°-Dreieck

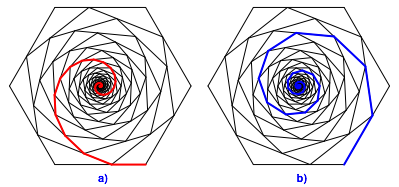
Abb. 12: Pythagoreische Spiralen

Für die Spiralenlängen können die Formeln (7) verwendet werden. Die rote Spirale (Abb. 12a) hat relativ zur Seitenlänge des Sechseckes die Spiralenlänge 3, die blaue Spirale (Abb. 12b) die Länge 5.

Die Tabelle 2 gibt weitere Beispiele.

u	v	a	b	c	srot	sblau
2	1	3	5	7	3	5
3	1	8	7	13	4	7/2
3	2	5	16	19	5/2	8
4	3	7	33	37	7/3	11
5	1	24	11	31	6	11/4
5	3	16	39	49	8/3	13/2
5	4	9	56	61	9/4	14
6	1	35	13	43	7	13/5
6	5	11	85	91	11/5	17
7	2	45	32	67	9/2	16/5
7	3	40	51	79	10/3	17/4
7	5	24	95	109	12/5	19/2
7	6	13	120	127	13/6	20
8	1	63	17	73	9	17/7
8	3	55	57	97	11/3	19/5
8	7	15	161	169	15/7	23
9	1	80	19	91	10	19/8
9	2	77	40	103	11/2	20/7
9	4	65	88	133	13/4	22/5
9	5	56	115	151	14/5	23/4
9	7	32	175	193	16/7	25/2
9	8	17	208	217	17/8	26
10	3	91	69	139	13/3	23/7
10	9	19	261	271	19/9	29

Tab. 2: Beispiele im Sechseck

Websites

Hans Walser: Spiralen im regelmäßigen Vieleck

www.walser-h-m.ch/hans/Miniaturen/S/Spiralen_reg_Vieleck/Spiralen_reg_Vieleck.htm

Hans Walser: Pythagoreische Spiralen

www.walser-h-m.ch/hans/Miniaturen/P/Pythagoreische_Spiralen/Pythagoreische_Spiralen.htm

Hans Walser: Pythagoreische 60°- und 120°-Dreiecke

http://www.walser-h-m.ch/hans/Miniaturen/P/Pyth-60-Dreiecke/Pyth-60-Dreiecke.htm