Hans Walser, [20140424]

p,q-Matrix

Anregung: R. S., C.

1 Worum geht es?

Für und untersuchen wir die Matrix:

Die Matrix hat die Zeilensummen und Spaltensummen 1. Sie ist also ein Sonderfall einer stochastischen Matrix.

Es entsteht ein Link zur Binomialverteilung.

2 Daten

Determinante:

Eigenwerte und Eigenvektoren:

Charakteristische Gleichung:

Eigenwerte:

Bemerkung: Jede stochastische Matrix hat einen Eigenwert 1.

Eigenvektoren:

Bemerkung: Die Matrix A ist symmetrisch. Bei jeder symmetrischen Matrix sind die Eigenvektoren orthogonal.

3 Beispiel

Wir wählen , also:

,

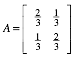Potenzen der Matrix und Umformung:

Matrix:

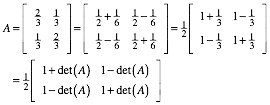
Quadrat der Matrix:

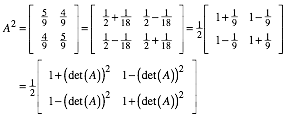
Dritte Potenz:

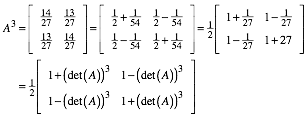
Wir sehen, wie der Hase läuft. Vermutung:

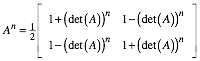
4 Beweis

Die Vermutung stimmt allgemein für unsere p,q-Matrix. Wegen haben wir also die Vermutung:

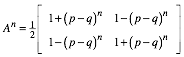
Beweis induktiv, wobei wir dauernd die Relation verwenden:

(I) Verankerung:

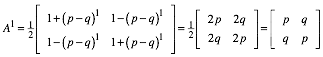
(II) Induktionsschritt:

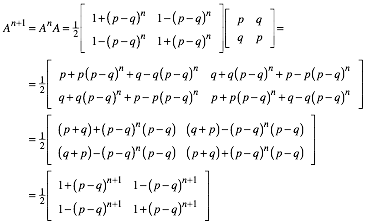
Damit ist die Vermutung bewiesen.

5 Grenzwert

Für und ist und damit:

6 Lineare Abbildung

Wir arbeiten exemplarisch mit der Matrix:

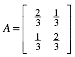
Im folgenden ist das Urbild grün, das Bild bei der Abbildung mit A rot und das Bild bei der Abbildung mit blau eingezeichnet.

Die Abbildung 1 zeigt die Bilder des Einheitsquadrates:

Abb. 1: Bilder des Einheitsquadrates

Die Abbildung 2 zeigt die Bilder des Einheitskreises.

Abb. 2: Bild des Einheitskreises

Wir sehen eine Kontraktion zur 45°-Geraden. Diese hat die Richtung des ersten Eigenvektors. Sie ist Fixpunktgerade der Abbildung. In Richtung des zweiten Eigenvektors haben wir jeweils eine Kontraktion mit dem Faktor . Dies ist der zweite Eigenwert.

7 Konjugation der Matrix

Die Abbildungen 1 und 2 legen nahe, die Situation in einem gedrehten Koordinatensystem zu beschreiben, dessen Achsen die Richtungen der Eigenvektoren haben (Abb. 3).

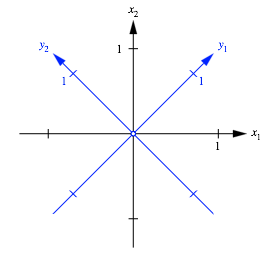
Abb. 3: Neues Koordinatensystem

Für die Umrechnung brauchen wir die Drehmatrix:

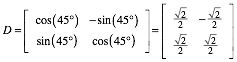
Die Matrix welche die Abbildung im neuen Koordinatensystem beschreibt finden wir durch Konjugation:

In der Hauptdiagonalen von stehen nun die beiden Eigenwerte der Matrix. Auch das Abbildungsverhalten ist sofort klar: In Richtung der ersten Achse passiert nichts, in Richtung der zweiten Achse haben wir den Kontraktionsfaktor .

Das Potenzieren wir nun einfach:

Durch Rückkonjugation erhalten wir die Situation im ursprünglichen Koordinatensystem:

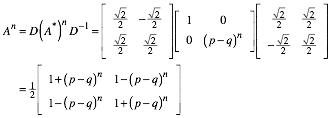
Damit hätten wir uns den Induktionsbeweis sparen können.

Weiter ist wegen :

Daraus erhalten wir ebenfalls durch Rückkonjugation:

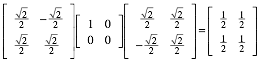
8 Binomialverteilung

Wir kehren nun zurück zur ursprünglichen Matrix:

Wir interpretieren p als Wahrscheinlichkeit eines Erfolges bei einem Bernoulli-Experiment und q entsprechend als Wahrscheinlichkeit eines Misserfolges.

Für das Quadrat der Matrix A erhalten wir:

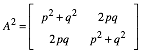
In der ersten Zeile ist das erste Element die Wahrscheinlichkeit, bei einer zweistufigen Bernoulli-Kette entweder zwei Erfolge oder zwei Misserfolge zu haben, das zweite Element ist die Wahrscheinlichkeit, genau einen Erfolg und einen Misserfolg zu haben. In der zweiten Zeile ist die Situation umgekehrt.

Weiter mit der dritten Potenz:

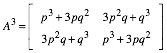
Hier ist die Wahrscheinlichkeit, bei drei Versuchen entweder drei oder genau einen Erfolg zu haben.

Allgemein ist in das erste Element in der obersten Zeile die Wahrscheinlichkeit, bei n Versuchen eine Anzahl Erfolge aus zu haben, und das andere Element der obersten Zeile die Gegenwahrscheinlichkeit, also die Wahrscheinlichkeit, bei n Versuchen eine Anzahl Erfolge aus zu erhalten.

Beweis mit Induktion.

Da für die beiden Elemente den Limes haben, heißt das, dass sich die beiden Wahrscheinlichkeiten annähern. Dies ist auch intuitiv klar.