Hans Walser, [20190627]
Quibla
Anregung: Vortrag von Ph. U., F.
1 Worum geht es?
Berechnung der Quibla, das hei§t der Richtung des Gro§kreisbogens nach Mekka.
2 Daten und Bezeichnungen
Kaaba in Mekka, Koordinaten: 21¡ 25Õ 21ÕÕ N, 39¡ 49Õ 34ÕÕ E
Umrechnung ins Bogenma§: 0.37389316 N, 0.69509677 E
Standortkoordinaten: phi, lambda
3 Sphrisches Dreieck
Wir arbeiten mit dem sphrischen Dreieck ABC, wobei:
A = Standort
B = Kaaba in Mekka
C = Nordpol
Die Abbildung 1 skizziert die Situation.
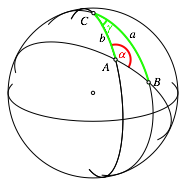
Abb. 1: Situation
Aus den
geografischen Breiten von Mekka und dem Standort lassen sich a und b berechnen (Ergnzung auf ¹/2). Die Differenz der geografischen
Lngen ergibt ![]() .
.
Gesucht
ist ![]() .
.
4 Sphrische Trigonometrie
Die passende Formel (siehe Formelsammlung) ist:
![]()
Dies kann umgeformt werden zu:
![]()
5 Beispiele
Die Richtung wird auf einem Kompass angegeben.
5.1 Saarbrcken
Koordinaten: 49.256577 N, 7.045378 E
Wir erhalten das Azimut 125.1277¡ (Abb. 2).
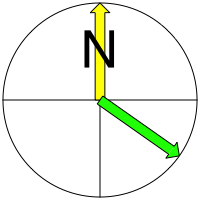
Abb. 2: Saarbrcken
5.2 Gleiche geografische Breite wie Mekka
Koordinaten: 21¡ 25Õ 21ÕÕ N, 10¡ 49Õ 34ÕÕ E
Wir erhalten das Azimut 84.6040¡ (Abb. 3). Die Richtung geht also nicht genau nach Osten, sondern ãoben durchÒ. Genau nach Osten wre ein Breitenkreis, aber kein Gro§kreis.
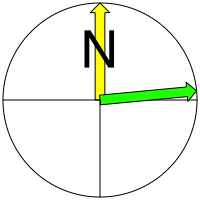
Abb. 3: Gleiche geografische Breite wie Mekka
5.3 stlich von Mekka
Harwan Garden, Koordinaten: 34¡09'34.9"N 74¡54'13.8"E. Wir befinden uns nrdlich und stlich von Mekka.
Wir erhalten aber formelm§ig das Azimut 76.7934¡ (Abb. 4).
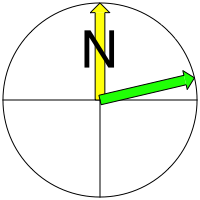
Abb. 4: stlich von Mekka?
Das irritiert, denn der grne Pfeil sollte nach Westen zeigen. Wir sind hier in der klassischen Tangensfalle. Der Tangens und der Kotangens haben einen sehr eingeschrnkten Bijektivittsbereich. Man muss mit Zusatzbedingungen (Vorzeichen) allenfalls 180¡ addieren. Man kann es aber auch so sehen: Es wird hier der gro§e Gro§kreisbogen, also der ãhintenherumÒ, gewhlt.
6
Zeichnerische Lsung
6.1 In der stereografischen
Projektion
Auf einer
Karte in stereografischer Projektion kann die Qibla bestimmt werden wie folgt
(Abb. 5).
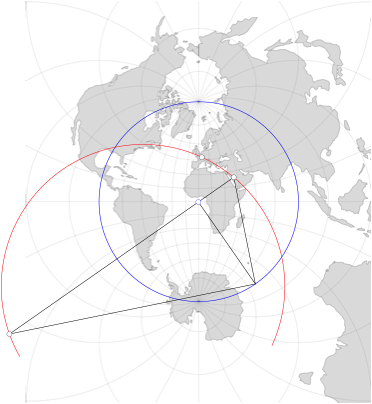
Abb.
5: Grafische Bestimmung
á
Diametraler Punkt zu Mekka (im
Prinzip Spiegelung am Hauptkreis, aber auf
die andere Seite)
á
(Planimetrischer)
Kreis durch Standort, Mekka und diametralen Punkt von
Mekka. Dies ist das stereografische Bild des gesuchten Gro§kreises.
á
Da die stereografische Projektion
winkeltreu (conformal) ist, kann der Winkel zum Meridian durch den Standort
abgelesen werden.
6.2 Ohne Karte
Das
Kartenbild ist nicht erforderlich. Bei Kenntnis von phi und lambda kann die
Position in der stereografischen Projektion gem§ Abbildung 6 eingezeichnet
werden.
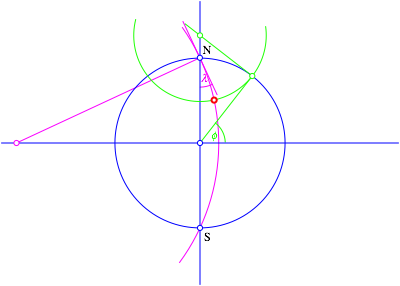
Abb.
6: Konstruktion in der stereografischen Projektion
7 Formeln der sphrischen Geometrie
7.1 Sphrische Dreiecke und Vielecke
![]()
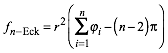
7.2 Sphrische Trigonometrie
Seiten-Cosinus-Satz
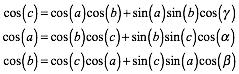
Winkel-Cosinus-Satz
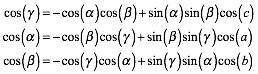
Sinus-Satz
![]()
Cotangens-Satz, erste Gruppe
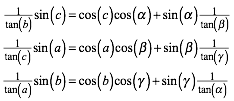
Cotangens-Satz, zweite Gruppe
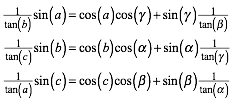
7.3 Sphrischer Pythagoras
![]()
Websites
Kartenprojektionen
http://swai.ethz.ch/swaie/MapProjector/MapProjector.de.html