Hans Walser, [20230826]
Quadrat auf Rechteck
1 Worum es geht
Eine Gleichflächenbedingung führt zum Goldenen Schnitt.
2 Problemstellung
Auf einem blauen Rechteck sitzt mittig ein rotes Quadrat. Die Figur passt in ein umfassendes Quadrat (Abb. 1). Wann haben das blaue Rechteck und das rote Quadrat denselben Flächeninhalt?

Abb. 1: Quadrat auf Rechteck
Die Abbildung 2 zeigt die Kinematik der Problemstellung.

Abb. 2: Kinematik
3 Bearbeitung
Das umfassende Quadrat sei das Einheitsquadrat, h die Höhe des blauen Rechteckes. Die Flächengleichheitsbedingung besagt:
h = (1 – h)2
Die für uns relevante Lösung dieser quadratischen Gleichung ist h = 1/Φ2 ≈ 0.3820. Dabei ist Φ der Goldene Schnitt, also Φ = (1 + √5)/2 ≈ 1.6180.
4 Mach mal Pause
In der Abbildung 3 ist bei der Lösung ein Zwischenhalt.

Abb. 3: Zwischenhalt bei der Lösung
5 Gemeinsame Zerlegung
Die Abbildung 4 illustriert die Flächengleichheit.
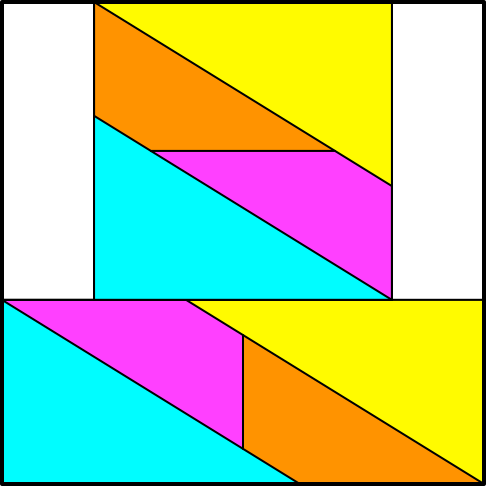
Abb. 4: Gemeinsame Zerlegung
Weblink
Hans Walser: Miniaturen: Goldener Schnitt
http://www.walser-h-m.ch/hans/Miniaturen_Uebersicht/Goldener_Schnitt/index.html