1 Worum geht es?

Einem Dreieck ist ein Quadrat einzubeschreiben, das auf einer Dreiecksseite sitzt (Abb. 1).

Abb. 1: Quadrat im Dreieck

2 Konstruktion

Wir arbeiten mit den Bezeichnungen der Abbildung 2a. Das Quadrat soll auf der Seite c aufsitzen.

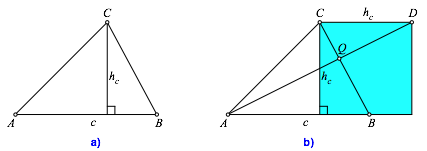
Abb. 2: Bezeichnungen. Höhenquadrat

Wir zeichnen nun das Höhenquadrat mit der Seite h_c (Abb. 2b). Der Schnittpunkt Q der Geraden BC und AD ist eine Ecke des gesuchten Quadrates (Abb. 3a). Das Höhenquadrat ist das Modellquadrat, das durch die zentrische Streckung mit dem Zentrum A in die richtige Größe und Lage gebracht wird.

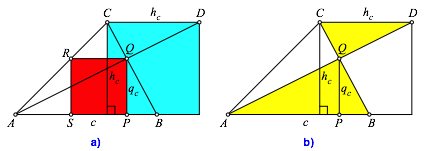
Abb. 3: Gesuchtes Quadrat. Ähnliche Dreiecke

3 Rechnung

Zur Berechnung der Quadratseite q_c arbeiten wir mit den beiden gelben Dreiecken der Abbildung 3b. Aus der Ähnlichkeit dieser Dreiecke folgt:

(1)

Daraus erhalten wir:

(2)

4 Diskussion

In (2) haben wir „Produkt durch Summe“.

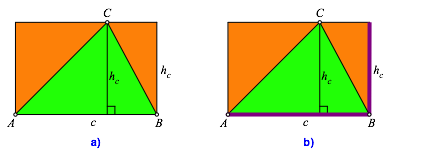
Abb. 4: Rechteck

Das Produkt im Zähler ist das Doppelte der Dreiecksfläche und kann durch ein Rechteck dargestellt werden (Abb. 4a). Die Summe im Nenner ist der halbe Umfang dieses Rechteckes (Abb. 4b).

Aus (2) folgt weiter, dass sich die Quadratseite q_c nicht ändert, wenn die Ecke C auf einer Parallelen zur Grundseite c bewegt wird (Abb. 5).

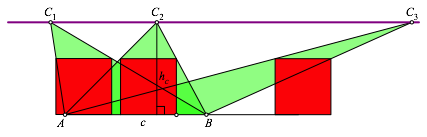
Abb. 5: Invariante Quadratseite

Die Formel (2) kann umgeformt werden zu:

(3)

Die Quadratseite q_c ist also das halbe harmonische Mittel von c und h_c.

Durch zyklische Vertauschung erhalten wir allgemein:

(4)

Websites

Thomas Jahre, Aufg. 56 - 668

https://www.schulmodell.eu/images/stories/mathe/wochenaufgabe/668.jpg

Hans Walser: Quadrat im Dreieck

http://www.walser-h-m.ch/hans/Miniaturen/Q/Quadrat_im_Dreieck/Quadrat_im_Dreieck.htm