Hans Walser, [20190415]
Quadrat <–> FŸnfeck
Anregung: Patrik G. K. Wiesner, BSc ETHZ, Davidgasse 42, A - 1100 Wien
1 Worum geht es?
Gesucht ist eine gemeinsame Zerlegung eines Quadrates und eines flŠchengleichen regelmŠ§igen FŸnfeckes.
2 Lšsungen
Im Folgenden einige Lšsungen.
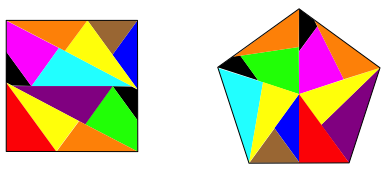
Abb. 1: Erste Lšsung
In der Lšsung der Abbildung 1 haben wir nur wenige Formen, die in verschiedenen Farben und Positionen erscheinen.
Abb. 2: Zweite Lšsung
Bei der Lšsung der Abbildung 2 werden viel mehr Teile benštigt. Beim Quadrat haben wir links oben eine kleines schwarzes und anschlie§end ein kleines himmelblaues Dreieck. Beim FŸnfeck ist das schwarze Dreieck an der Spitze oben und das himmelblaue in der Mitte.
Etliche Farben mussten mehrfach, das hei§t fŸr nicht kongruente Teile, verwendet werden.
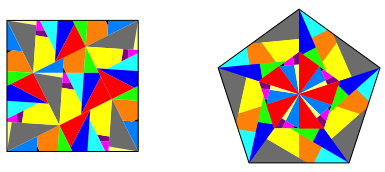
Abb. 3: Dritte Lšsung
In der Lšsung der Abbildung 3 haben wir nur elf verschiedene Teile, aber jedes Teil kommt fŸnfmal vor.
Abb. 4: Selbe Grundidee wie bei der Abbildung 3
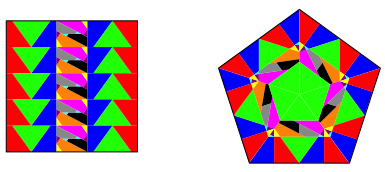
Abb. 5: Hohe Symmetrie bei Quadrat und FŸnfeck
Bei der Lšsung der Abbildung 5 haben wir hohe Symmetrien sowohl beim Quadrat wie auch beim FŸnfeck. Es sind acht Formen im Spiel. Jede Form erscheint zehn Mal.
Abb. 6: Hohe Symmetrie
Die Lšsung der Abbildung 6 ist nach derselben Grundidee gebaut wie die Lšsung der Abbildung 5. Es sind sechs Formen im Spiel. Ein sehr kleines Dreieck sieht man kaum.
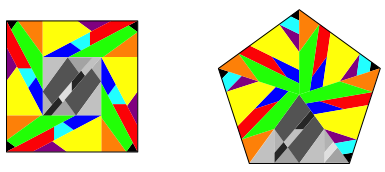
Abb. 7: Wie steht es mit den Symmetrien?
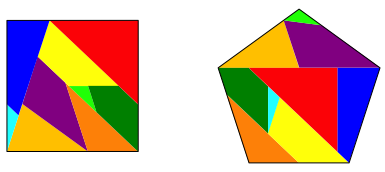
Abb.8: Lšsung
Wir haben insgesamt nur neun Teile. Das ist die Minimallšsung der von mir gefundenen Lšsungen.
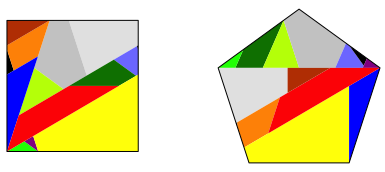
Abb. 9: Lšsung
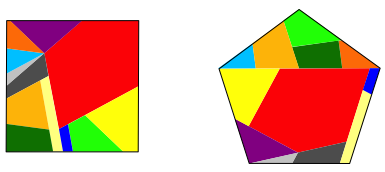
Abb. 10: Lšsung mit einem gro§en roten Fleck
Weblinks
Hans Walser: Dreieck, Quadrat, FŸnfeck
www.walser-h-m.ch/hans/Miniaturen/D/Dreieck-Quadrat-Fuenfeck/Dreieck-Quadrat-Fuenfeck.htm
Patrick Wiesner, Homepage