Hans Walser, [20160434]
Quadrate ansetzen
1 Worum geht es?
Einem beliebigen Vieleck setzen wir an den Seiten Quadrate an. Dann wiederholen wir das Quadrate-Ansetzen. Es entstehen Flchenverhltnisse, die mit den Fibonacci-Zahlen zu tun haben (Posamentier and Lehmann 2007), (Walser 2012).
2 Beispiel
Wir arbeiten exemplarisch mit einem Dreieck. Erste Runde
Einem beliebigen schwarzen Dreieck setzen wir an den Seiten rote Quadrate an (Abb. 1). Das sind wir von der Pythagoras-Ikone her gewohnt, aber in unserem Fall braucht das Dreieck nicht rechtwinklig zu sein.

Abb. 1: Rote Quadrate
Mit s1 bezeichnen wir die Flchensumme der drei roten Quadrate.
2.1 Zweite Runde
Nun setzen wir einen Kranz von grnen Quadraten an gem§ Abbildung 2.
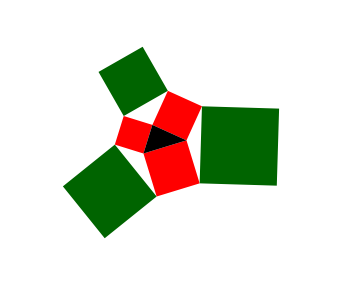
Abb. 2: Kranz von grnen Quadraten
Mit s2 bezeichnen wir die Flchensumme der drei grnen Quadrate.
2.2 Blaue Runde

Abb. 3: Kranz von blauen Quadraten
Die blauen Quadrate basieren je auf einer Ecke eines grnen und eines roten Quadrates. Wir greifen also auf die zwei vorangehenden Quadratkrnze zurck. Das erinnert an die Rekursion der Fibonacci-Zahlen.
Mit s3 bezeichnen wir die Flchensumme der drei blauen Quadrate.
2.3 Himmelblaue Runde

Abb. 4: Himmelblaue Runde
Die himmelblauen Quadrate basieren wiederum je auf einer Ecke der beiden vorangehenden Quadratkrnze.
Mit s4 bezeichnen wir die Flchensumme der drei himmelblauen Quadrate.
2.4 Magenta
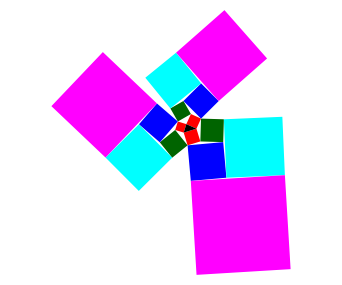
Abb. 5: Magenta Runde
Mit s5 bezeichnen wir die Flchensumme der drei magenta Quadrate.
2.5 Goldgelb
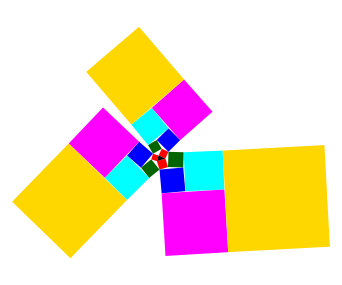
Abb. 6: Goldgelbe Runde
3 Flchenverhltnis
Wir erhalten experimentell unabhngig von der Form des schwarzen Basisdreieckes das Flchenverhltnis:
![]() (1)
(1)
Somit stellen sich zwei Fragen:
Wie lassen sich diese experimentellen Befunde beweisen?
Was hat es mit der Zahlenfolge 1, 3, 7, 19, 49, 129, ... auf sich?
4 Beweis
Fr den Beweis arbeiten wir mit einem Hilfssatz, dem Max-und-Moritz-Theorem.
4.1 Das Max-und-Moritz-Theorem
Wir beginnen mit zwei Quadraten (blau in Abb. 7), die an einer Ecke gelenkig verbunden sind. Dann fgen wir zwei weitere Quadrate an (rot in Abb. 7).
In dieser Situation gilt das Max-und-Moritz-Theorem:
rot = zwei mal blau (2)

Abb. 7: rot = zwei mal blau
Fr den Beweis arbeiten wir mit den Bezeichnungen der Abbildung 8.
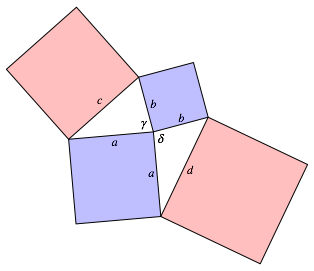
Abb. 8: Bezeichnungen
Die
Winkel ![]() und
und ![]() ergnzen
sich auf 180¡. Daher ist:
ergnzen
sich auf 180¡. Daher ist:
![]() (3)
(3)
Aus dem Kosinus-Satz ergibt sich:
![]() (4)
(4)
Wegen (3) ergibt sich durch Addition der beiden Zeilen von (4):
![]() (5)
(5)
Damit ist das Max-und-Moritz-Theorem bewiesen. Es wird im Folgenden andauernd verwendet.
Noch eine neckische Zusatzbemerkung (Abb. 9). Das Lot auf die eine rote Quadratseite halbiert die andere rote Quadratseite (und umgekehrt). Beweis? Dieser Sachverhalt wird im Folgenden nur zur Przisierung der Relation gegenberliegende Quadrate verwendet.
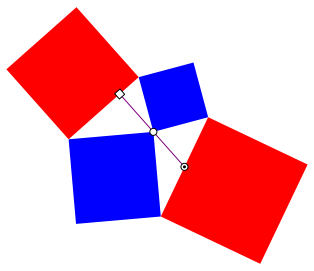
Abb. 9: Lot und Seitenhalbierende
Nun zurck zu unserem Dreieck.
4.2 Grne Runde
Aus der Disposition der Abbildung 2 ergibt sich aus dem Max-und-Moritz-Theorem, dass jedes grne Quadrat zusammen mit dem gegenberliegenden roten Quadrat jeweils flchengleich ist wie das Doppelte der beiden benachbarten Quadrate. Aufsummieren ergibt:
![]() (6)
(6)
Damit ist das erste Verhltnis von (1) abgehakt.
4.3 Blaue Runde
Gem§ Abbildung 3 ist jedes blaue Quadrat zusammen mit dem gegenberliegenden roten Quadrat flchenm§ig doppelt so gro§ wie das grne und das rote Quadrat, die eine gemeinsame Ecke auf dem Lot haben.
Aufsummieren ergibt daher:
![]() (7)
(7)
Damit ist das zweite Verhltnis von (1) abgehakt.
4.4 Himmelblaue Runde
Gem§ Abbildung 4 ist jedes himmelblaue Quadrat zusammen mit dem gegenberliegenden roten Quadrat flchenm§ig doppelt so gro§ wie das anschlie§ende blaue und grne Quadrat. Somit nach dem Max-und-Moritz-Theorem und Aufsummieren:
![]() (8)
(8)
5 Rekursion
Die himmelblaue Runde ist bereits typisch fr alle folgenden Runden. Fr n > 2 gilt:
![]() (9)
(9)
Damit haben wir die Rekursionsformel fr unsere Folge sn gefunden:
![]() (10)
(10)
Im Unterschied zur Fibonacci-Rekursion brauchen wir die drei vorangehenden Folgenglieder und daher auch drei Startwerte.
Die Tabelle 1 zeigt die ersten 20 Folgenglieder.
|
n |
sn |
|
n |
sn |
|
1 |
1 |
|
11 |
15841 |
|
2 |
3 |
|
12 |
41473 |
|
3 |
7 |
|
13 |
108577 |
|
4 |
19 |
|
14 |
284259 |
|
5 |
49 |
|
15 |
744199 |
|
6 |
129 |
|
16 |
1948339 |
|
7 |
337 |
|
17 |
5100817 |
|
8 |
883 |
|
18 |
13354113 |
|
9 |
2311 |
|
19 |
34961521 |
|
10 |
6051 |
|
20 |
91530451 |
Tab. 1: Folgenglieder
Die Folge hat die explizite Formel (bliche Herleitung):
![]() (11)
(11)
Mit der Schreibweise des Goldenen Schnittes (Posamentier and Lehmann 2012), (Walser 2013)
![]() (12)
(12)
kann die explizite Form geschrieben werden wie folgt:
![]() (13)
(13)
6 Die Fibonacci-Packung
Die Abbildung 10 zeigt die Fibonacci-Packung.
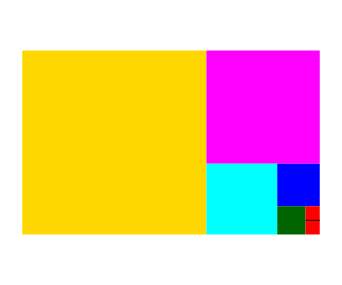
Abb. 10: Fibonacci-Packung
Die Quadrate haben der Reihe nach die Seitenlngen:
1, 1, 2, 3, 5, 8, 13, ... (14)
Das sind die Fibonacci-Zahlen. Die Quadrate haben daher der Reihe nach die Flcheninhalte:
1, 1, 4, 9, 25, 64, 169, ... (15)
Diese Folge hat ebenfalls die Rekursion (10) wie unsere Folge sn.
In der Abbildung 6 erkennen wir dreimal nherungsweise diese Fibonacci-Packung. Die drei Packungen haben aber die roten Startquadrate gemeinsam.
7 Andere Vielecke
Die Abbildungen 11 und 12 zeigen das analoge Vorgehen basierend auf einem beliebigen Viereck oder Siebeneck. Dabei ergeben sich berlappungen der Quadrate.
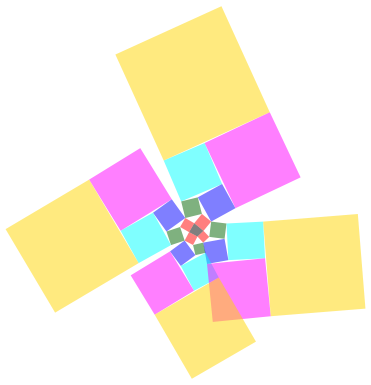
Abb. 11: Viereck als Ausgangsfigur

Abb. 12: Siebeneck als Ausgangsfigur
Wir erkennen wiederum die nherungsweisen Fibonacci-Packungen.
Die Flchensummen haben ebenfalls die Rekursion (10), aber andere Startwerte. Die Startwerte sind nicht mehr so schn wie im Falle eines Dreiecks als Startfigur.
Literatur
Posamentier, Alfred S. and Lehmann, Ingmar (2007): The (Fabulous) Fibonacci Numbers. Amherst, N.Y., Prometheus Books.
Posamentier, Alfred S. and Lehmann, Ingmar (2012): The Glorious Golden Ratio. Amherst, N.Y., Prometheus Books.
Walser, Hans (2012): Fibonacci. Zahlen und Figuren. Leipzig, EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-60-8.
Walser, Hans (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wu§ing ber populrwissenschaftliche Mathematikliteratur aus Leipzig. Edition am Gutenbergplatz, Leipzig. ISBN 978-3-937219-85-1.