1 Worum geht es?

Quadrate im und am rechtwinkligen Dreieck führen zu kollinearen Punkten und kopunktalen Geraden.

2 Die Quadrate

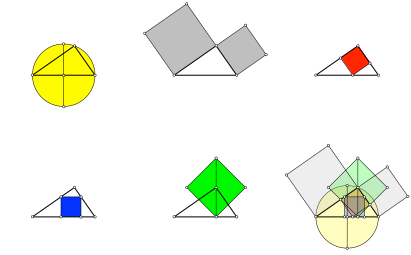
Abb. 1: Quadrate im und am rechtewinkligen Dreieck

Zu einem rechtwinkligen Dreieck zeichnen wir:

1. Den Thaleskreis

2. Die beiden Kathetenquadrate

3. Das einbeschriebene Quadrat in der Ecke mit dem rechten Winkel (rot).

4. Das einbeschriebene Quadrat auf der Hypotenuse (blau). Das blaue Quadrat ist kleiner als das rote Quadrat.

5. Das Quadrat mit dem Mittelpunkt in der Ecke mit dem rechten Winkel und einer Ecke im Fußpunkt der auf der Hypotenuse stehenden Höhe (grün).

Nun zeichnen wir die Überlagerung all dieser Figuren (Abb. 2).

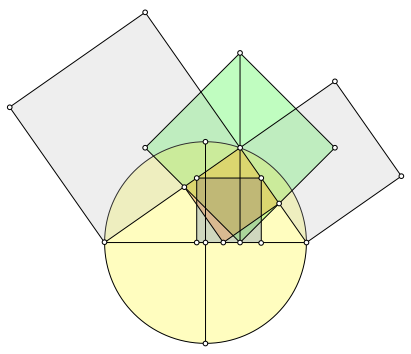
Abb. 2: Überlagerung

3 Kollineare Punkte und kopunktale Geraden

In der Figur hat es etliche Beispiele von kollinearen Punkten, also von drei oder mehr Punkten auf derselben Geraden (Abb. 3). Die betreffenden Geraden sind rot eingetragen.

Ebenso ergeben sich dann kopunktale Geraden, also drei oder mehr Geraden durch denselben Punkt. Die betreffenden Punkte sind rot markiert.

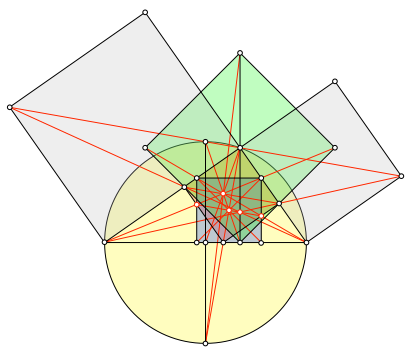
Abb. 3: Kollineare Punkte und kopunktale Geraden

4 Animation

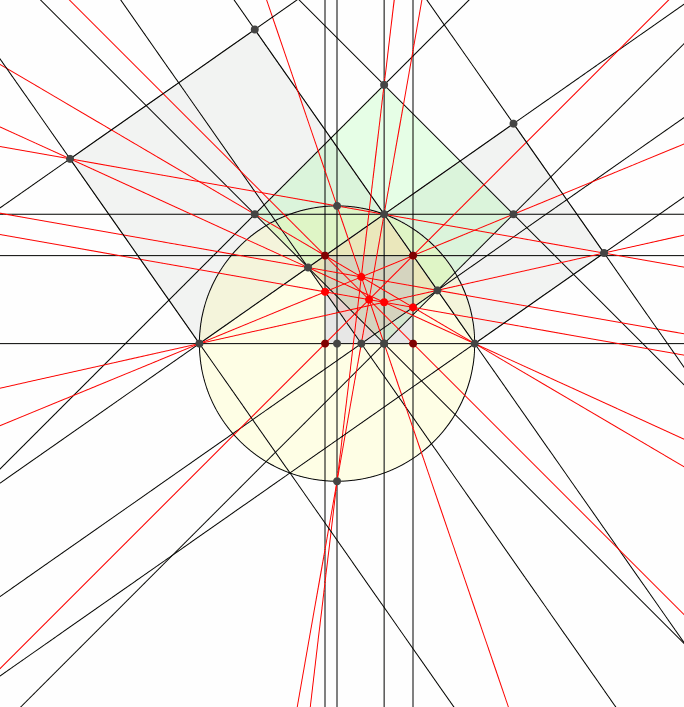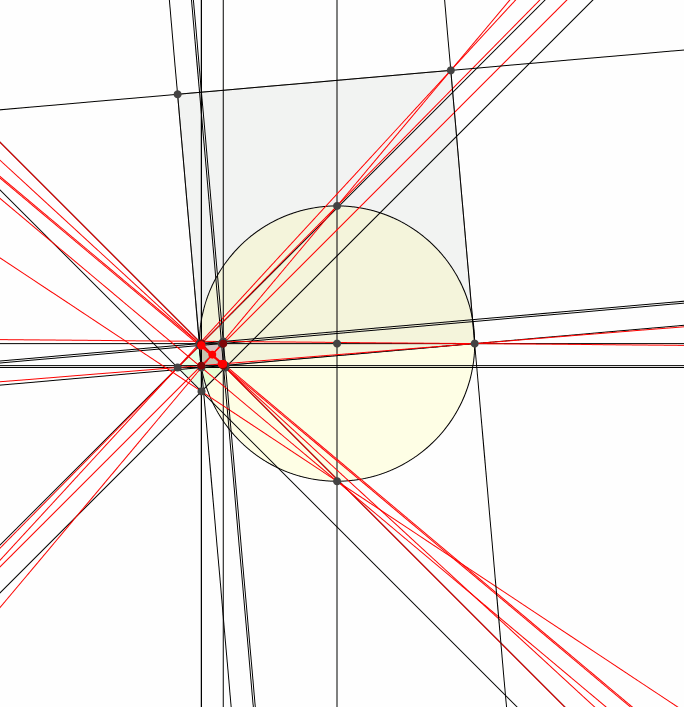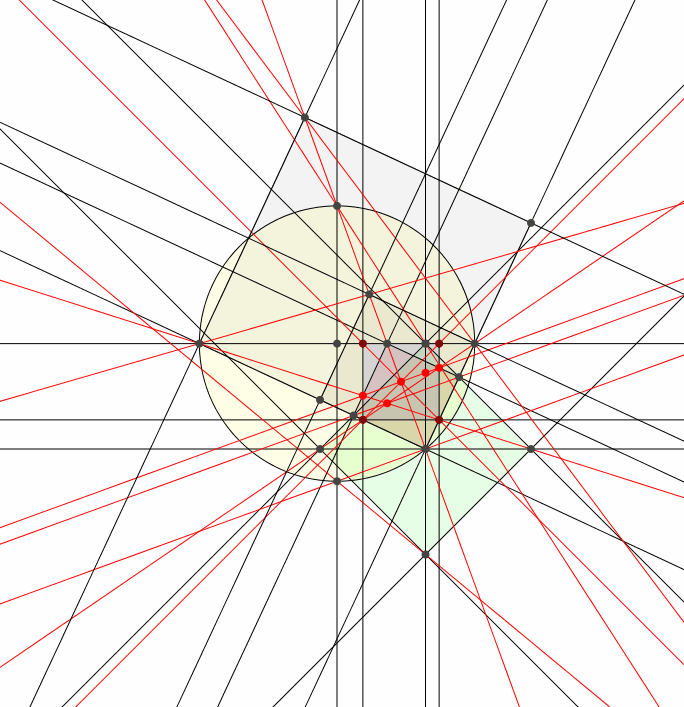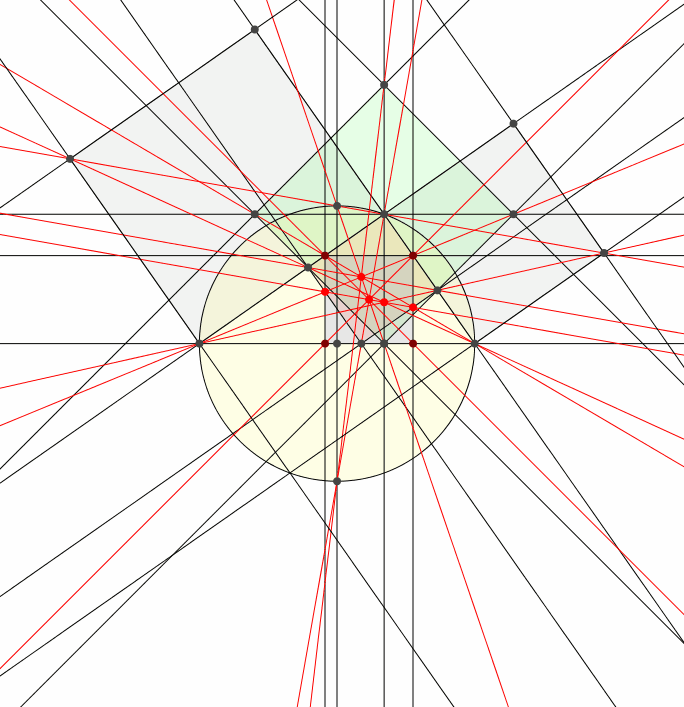
Abb. 4: Kollineare Punkte und kopunktale Geraden

Literatur

Walser, Hans (2012): 99 Schnittpunkte. Beispiele – Bilder – Beweise. 2. Auflage. EAGLE, Edition am Gutenbergplatz: Leipzig. ISBN 978-3-937219-95-0

Websites

Hans Walser: Euklid-Punkt

http://www.walser-h-m.ch/hans/Miniaturen/E/Euklid-Punkt2/Euklid-Punkt2.html

Hans Walser: Euklid-Punkt und seine Bahnkurven

http://www.walser-h-m.ch/hans/Miniaturen/E/Euklid-Punkt/Euklid-Punkt.html

Hans Walser: Miniaturen: Pythagoras, Flächensummen und rechtwinkliges Dreieck

http://www.walser-h-m.ch/hans/Miniaturen_Uebersicht/Pythagoras/index.html

Hans Walser: Schnittpunkte

http://www.walser-h-m.ch/hans/Schnittpunkte/index.html