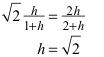1 Rhombus gesucht

Für welchen Rhombus sind die beiden Quadrate (Abb. 1) gleich groß?

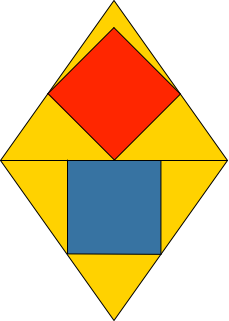
Abb. 1: Gleich große Quadrate

2 Hieb- und Stich-Rechnung

Wir arbeiten im Koordinatensystem der Abbildung 2.

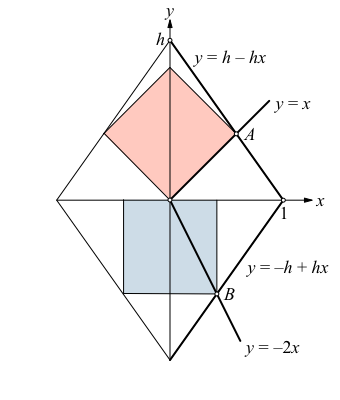
Abb. 2: Disposition

Für den Schnittpunkt A erhalten wir:

Damit ergibt sich für die Seitenlänge s_rot des roten Quadrates:

Für den Schnittpunkt B erhalten wir:

Damit ergibt sich für die Seitenlänge s_blau des blauen Quadrates:

Die Bedingung s_rot = s_blau ergibt:

Der gesuchte Rhombus hat also das Diagonalenverhältnis √2:1.

3 Bemerkungen zum Rhombus

Der Rhombus mit dem Diagonalenverhältnis √2:1 ergibt sich als Seitenmitten-Rhombus im DIN-Format (Abb. 3a). Die Seitenflächen des regelmäßigen Rhombendodekaeders sind ebenfalls Rhomben mit dem Diagonalenverhältnis √2:1 (Abb. 3b).

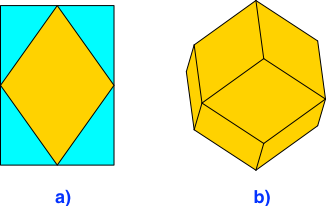
Abb. 3: DIN-Format und Rhombendodekaeder

4 Geometrische Konstruktion

Wir zeichnen zunächst zwei gleich große Quadrate in der gewünschten Position (Abb. 4a). Anschließend klappen wir das untere Quadrat nach oben (Abb. 4b). Damit haben wir genügend Informationen, die ober Hälfte des Rhombus zu zeichnen (Abb. 4c).

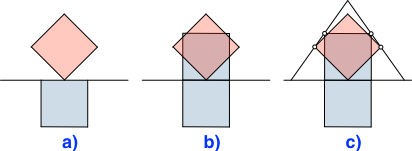
Abb. 4: Konstruktion

Durch Spiegeln ergibt sich die untere Hälfte.

5 Zerlegung

Bei gleich großen Quadraten sind auch die beiden Resteflächen des Rhombus oben und unten flächen- und damit zerlegungsgleich. Die Abbildung 5 zeigt eine gemeinsame Zerlegung der beiden Restflächen.

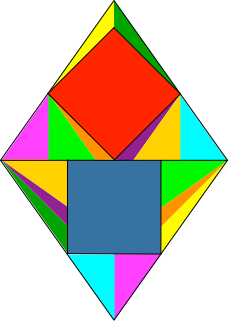
Abb. 5: Zerlegungsgleichheit

6 Teilpunkte

Die Eckpunkt der Quadrate unterteilen die Rhombenseiten im gleichen Verhältnis, nämlich √2:1.

Für den Teilpunkt A (Abb. 6a) ergibt sich dies aus dem hellblau eingezeichneten rechtwinkligen Dreieck. Es hat das Kathetenverhältnis √2:1. Die Winkelhalbierende des rechten Winkels teilt daher die Hypotenuse im selben Verhältnis.

Anschließend ergibt sich dieses Teilverhältnis für den Punkt B (Abb. 6b) aus den beiden gelb eingezeichneten rechtwinkligen Dreiecken, welche das Seitenverhältnis √2:1 haben (halbe Diagonale und halbe Seite in gleich großen Quadraten).

Abb. 6: Teilpunkte

7 Rhombenparkette

Die übereinstimmenden Teilpunkte haben zur Folge, dass in einem Rhombenparkett rote und blaue Quadrate gemeinsame Ecken haben (Abb. 7, 8 und 9).

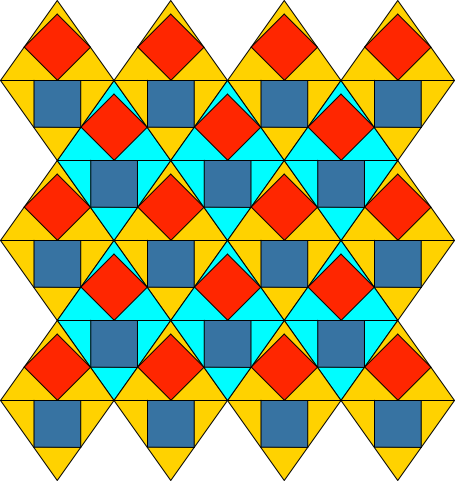
Abb. 7: Rhombenparkett

Abb. 8: Parkett mit gemeinsamen Zerlegungen

Abb. 9: Nur Farbe

Weblink

Hans Walser: Quadrat im Dreieck

http://www.walser-h-m.ch/hans/Miniaturen/Q/Quadrat_im_Dreieck/Quadrat_im_Dreieck.htm

Hans Walser: Quadratgleichheit

http://www.walser-h-m.ch/hans/Miniaturen/Q/Quadratgleichheit/Quadratgleichheit.html