Hans Walser, [20141214], [20150107]

Quadrate im Schachbrett

Anregung: Lange, Diemut (2014) und Rott, Benjamin (2014)

Idee: Mason, J, Burton, L., & Stacey, K. (1982/2010)

1 Die Frage

Wie viele Quadrate gibt es im Schachbrett (Abb. 1)?

Abb. 1: Schachbrett

2 Extremlösungen

2.1 Die Minimallösung

Wir beschränken uns auf das, was wir schwarz auf weiß vor Augen haben: Das kleine schwarze Quadrat und das große Rahmenquadrat. Also zwei Quadrate.

2.2 Die Maximallösung

Wir können beliebige Quadrate einzeichnen. Die Abbildung 2 zeigt ein Beispiel in rot.

Abb. 2: Beliebiges Quadrat

So gesehen, gibt es unendliche viele Quadrate im Schachbrett.

3 Restriktionen

3.1 Gitterlinien

Die Eckpunkte der Quadrate sollen auf Gitterlinien des Schachbrettes liegen. Die Abbildung 3 zeigt ein Beispiel.

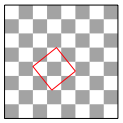
Abb. 3: Quadratecken auf Gitterlinien

Unter dieser Restriktion gibt es immer noch unendlich viele Quadrate.

3.2 Gitterpunkte

Anders wird die Sache, wenn wir die Quadratecken auf Gitterpunkte legen wollen (Abb. 4).

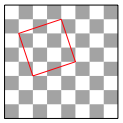
Abb. 4: Quadratecken in Gitterpunkten

Da wir im Schachbrett und auf seinem Rand insgesamt 81 Gitterpunkte haben, gibt es nur noch endlich viele Quadrate. Tatsächlich gibt es in einem quadratischen n✕n-Gitter genau

Quadrate mit den Ecken in den Gitterpunkten. In unserem Fall sind das

Quadrate.

4 Quadrat in vier Zügen

4.1 Turm

Die Abbildung 5 illustriert, wie ein Turm in vier Zügen ein Quadrat hinlegen kann.

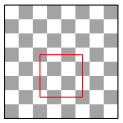
Abb. 5: Der Turm zeichnet ein Quadrat

Die Anzahl solcher Turmquadrate ist:

4.2 Läufer

Die Abbildung 6 zeigt ein Quadrat, das von einem Läufer gezeichnet wurde, der auf den weißen Feldern operiert.

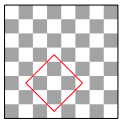
Abb. 6: Läufer

Solche Wege gibt es insgesamt , davon je 28 für Läufer auf weißen beziehungsweise schwarzen Feldern.

4.3 Dame

Da eine Dame sich wie ein Turm oder wie ein Läufer bewegen kann, hat sie 196 Möglichkeiten, ein Quadrat abzusetzen.

4.4 Springer

Die Abbildung 7 zeigt ein Quadrat, das durch einen Springer in vier Zügen gesprungen wurde.

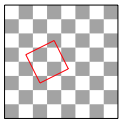
Abb. 7: Springer

Wenn ich richtig überlegt habe, gibt es solche Quadrate.

Der Springer kann auch in 8 Zügen ein Quadrat abstecken (Abb. 8).

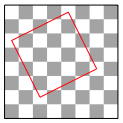
Abb. 8: Großes Springer-Quadrat

Solche großen Springer-Quadrate gibt es nur 8.

5 Würfel und Hyperwürfel

Meine Lehramtskandidaten stellten fest, dass ein Springer auch einen Würfel zeichnen kann (Abb. 9). Ich überlasse es der Leserin, die Anzahl solcher Würfel im Schachbrett zu bestimmen.

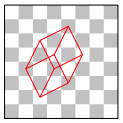
Abb. 9: Der Springer zeichnet einen Würfel

Allerdings muss er gelegentlich wieder zurückspringen, er kann nicht den ganzen Würfel in einem Durchgang zeichnen. Das können auch wir Menschen nicht, obwohl wir keine Rösser sind.

Der Springer kann sogar einen vierdimensionalen Hyperwürfel zeichnen (Abb. 10). Er braucht 32 Sprünge dazu.

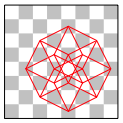
Abb. 10: 4d-Hyperwürfel

Und diesen Hyperwürfel schafft er sogar ohne Zurückspringen.

Nun ja, die Dame bringt ebenfalls einen vierdimensionalen Hyperwürfel zuwege (Abb. 11).

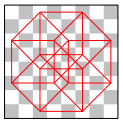
Abb. 11: 4d-Hyperwürfel der Dame

Literatur

Lange, Diemut (2014): Kooperationsarten in mathematischen Problemlöseprozessen. J Math Didakt 35. 173-204.

Mason, J, Burton, L., & Stacey, K. (1982/2010): Thinking mathematically (2nd Ed. 2010). Dorchester: Pearson.

Rott, Benjamin (2014): Mathematische Problembearbeitungsprozesse von Fünftklässlern – Entwicklung eines deskriptiven Phasenmodells. J Math Didakt 35. 252-282.