Hans Walser, [20130221]

Quadrate, Kreis und Goldener Schnitt

Es werden Konstruktionen des Goldenen Schnittes und des Goldenen Rechteckes vorgestellt, welche mit Quadraten und einem Kreis arbeiten.

Der Major ist jeweils blau, der Minor rot gezeichnet. Das Goldene Rechteck wird so golden wie möglich gezeichnet.

1 Zwei Quadrate

Abb. 1: Zwei Quadrate und ein Kreis

Hinter dieser Konstruktion steckt die klassische Konstruktion des Goldenen Schnittes.

2 Drei Quadrate

Wir zeichnen einen Stapel von drei Quadraten und zum mittleren Quadrat den Umkreis.

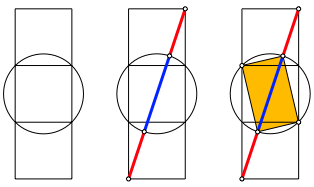
Abb. 2: Drei Quadrate und ein Kreis

Beweis durch Nachrechnen

3 Fünf Quadrate

Wir zeichnen ein Kreuz aus fünf Quadraten und dazu den Umkreis. Der Goldene Schnitt ergibt sich gemäß Abbildung 3. Beweis durch Nachrechnen.

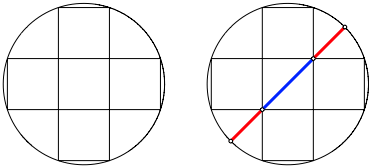
Abb. 3: Fünf Quadrate und ein Kreis

Das Goldene Rechteck finden wir gemäß Abbildung 4.

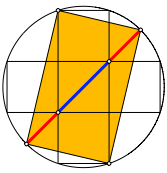
Abb. 4: Goldenes Rechteck

4 Fünf Quadrate und noch ein Quadrat

Wir zeichnen wieder ein Kreuz aus fünf Quadraten und dazu den Umkreis. In den Umkreis zeichnen wir ein weiteres (größeres) Quadrat ein gemäß Abbildung 5. Wir sehen den Goldenen Schnitt an allen Ecken und Enden.

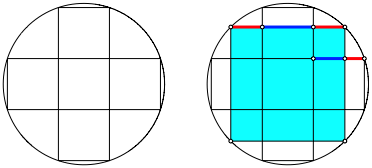
Abb. 5: Noch ein Quadrat

Der Beweis ergibt sich mit Strahlensätzen aus der Abbildung 3. Goldene Rechtecke finden wir en masse (Abb. 6).

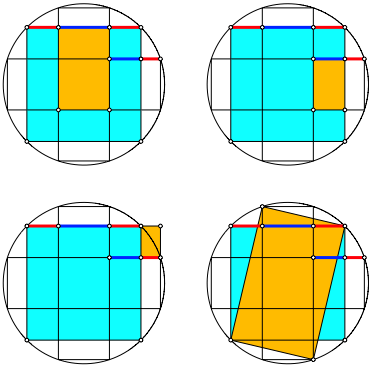
Abb. 6: Goldene Rechtecke

5 Der Major in der Mitte

Bei unseren Beispielen ist immer der Major in der Mitte, flankiert von zwei Minoren. Diese Situation haben wir auch in der Konstruktion von Odom (Abbildung 7).

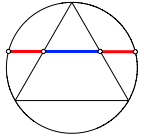
Abb. 7: Konstruktion von Odom