Hans Walser, [20070617a]

Grafische Lösung einer quadratischen Gleichung

Anregung: D. M. und M. P.

1 Problemstellung

Wir lösen die Gleichung:

Die Gleichung ist in einer in den Schulen unüblichen Form gegeben. Diese Form ist aber die eigentlich „natürliche“. Wir erhalten für die Lösungen:

und

Beispiel: In der quadratischen Gleichung ist und und daher:

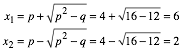
2 Grafische Lösungen

Wir besprechen drei verschiedene Methoden, die Gleichung grafisch zu lösen. Bei allen drei Methoden muss eine Einheitsstrecke e gegeben sein.

2.1 Die einfachste Methode

Diese Methode findet sich vielerorts in der Literatur. Wir verwenden ein kartesisches Koordinatensystem (damit ist auch die Einheitslänge gegeben). Über der Strecke AB mit und zeichnen wir den Thaleskreis und schneiden ihn mit der x-Achse. Die beiden Schnittpunkte sind und .

Die Figur illustriert den Fall . Es ist und .

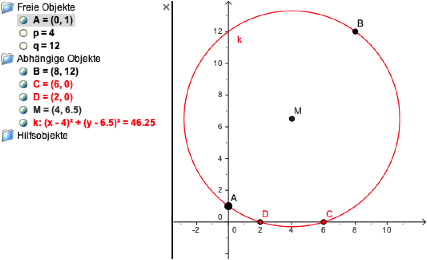
Konstruktion

Konstruktionsprotokoll:

Nr.	Name	Definition	Algebra
1	Punkt A	Punkt auf yAchse	A = (0, 1)
2	Zahl p		p = 4
3	Zahl q		q = 12
4	Punkt B	(2 p, q)	B = (8, 12)
5	Punkt M	Mittelpunkt von A, B	M = (4, 6.5)
6	Kreis k	Kreis mit Mittelpunkt M durch A	k: (x - 4)² + (y - 6.5)² = 46.25
7	Punkt C	Schnittpunkt von k, xAchse	C = (6, 0)
7	Punkt D	Schnittpunkt von k, xAchse	D = (2, 0)

2.1.1 Beweis

Es ist . Der Thaleskreis k hat den Radius und damit die Kreisgleichung:

Für den Schnitt mit der x-Achse setzen wir :

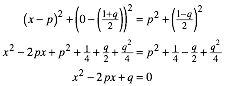
Die Schnittpunkte C und D führen also zu den Lösungen unserer quadratischen Gleichung.

Das Verfahren funktioniert auch für negative p und/oder q.

2.2 Zweimalige Anwendung des Höhensatzes

Wir zeichnen , und . Über der Strecke zeichnen wir den Thaleskreis und im Teilpunkt eine Senkrechte . Das gibt auf dem Thaleskreis den Punkt A. Nun eine Parallele a zur Basislinie durch A.

Auf der Parallelen a zeichnen wir den Punkt B mit der x-Koordinate p.

Nun zeichnen wir einen Kreis um B mit Radius p und schneiden ihn mit der x-Achse. Die Schnittpunkte C und D haben die x-Koordinaten beziehungsweise .

Die Figur illustriert den Fall . Es ist und .

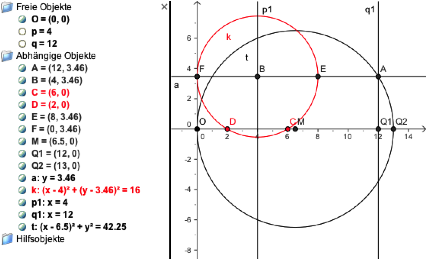
Konstruktion

Konstruktionsprotokoll:

Nr.	Name	Definition	Algebra
1	Zahl p		p = 4
2	Zahl q		q = 12
3	Punkt O		O = (0, 0)
4	Punkt Q1	(q, 0)	Q1 = (12, 0)
5	Punkt Q2	(q + 1, 0)	Q2 = (13, 0)
6	Punkt M	Mittelpunkt von O, Q2	M = (6.5, 0)
7	Gerade q1	x = q	q1: x = 12
8	Kreis t	Kreis mit Mittelpunkt M durch O	t: (x - 6.5)² + y² = 42.25
9	Punkt A	Schnittpunkt von t, q1	A = (12, 3.46)
10	Gerade a	Gerade durch A parallel zu xAchse	a: y = 3.46
11	Gerade p1	x = p	p1: x = 4
12	Punkt B	Schnittpunkt von a, p1	B = (4, 3.46)
13	Kreis k	Kreis mit Mittelpunkt B und Radius p	k: (x - 4)² + (y - 3.46)² = 16
14	Punkt C	Schnittpunkt von k, xAchse	C = (6, 0)
14	Punkt D	Schnittpunkt von k, xAchse	D = (2, 0)
15	Punkt E	Schnittpunkt von k, a	E = (8, 3.46)
15	Punkt F	Schnittpunkt von k, a	F = (0, 3.46)

2.2.1 Beweis

Aus dem Höhensatz im rechtwinkligen Dreieck ergibt sich . Aus dem Höhensatz im rechtwinkligen Dreieck ergibt sich .

Somit haben wir:

Somit ist eine Lösung der gegebenen quadratischen Gleichung. Analog für .

Das Verfahren funktioniert auch für , nicht aber für .

2.3 Stur nach Formel

Wir zeichnen die Lösungsformel und nach.

Die Figur illustriert den Fall . Es ist und .

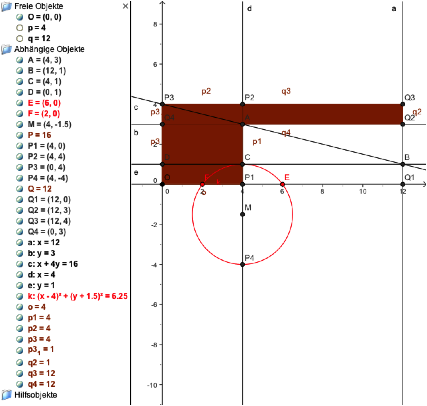
Konstruktion

Konstruktionsprotokoll:

Nr.	Name	Definition	Algebra
1	Zahl p		p = 4
2	Zahl q		q = 12
3	Punkt O		O = (0, 0)
4	Punkt P1	(p, 0)	P1 = (4, 0)
5	Punkt P2	(p, p)	P2 = (4, 4)
6	Punkt P3	(0, p)	P3 = (0, 4)
7	Punkt P4	(p, -p)	P4 = (4, -4)
8	Vieleck P	Vieleck O, P1, P2, P3	P = 16
8	Strecke o	Strecke[O, P1] von Vieleck P	o = 4
8	Strecke p1	Strecke[P1, P2] von Vieleck P	p1 = 4
8	Strecke p2	Strecke[P2, P3] von Vieleck P	p2 = 4
8	Strecke p3	Strecke[P3, O] von Vieleck P	p3 = 4
9	Punkt Q1	(q, 0)	Q1 = (12, 0)
10	Punkt Q2	(q, p - 1)	Q2 = (12, 3)
11	Punkt Q3	(q, p)	Q3 = (12, 4)
12	Punkt Q4	(0, p - 1)	Q4 = (0, 3)
13	Vieleck Q	Vieleck Q4, Q2, Q3, P3	Q = 12
13	Strecke q4	Strecke[Q4, Q2] von Vieleck Q	q4 = 12
13	Strecke q2	Strecke[Q2, Q3] von Vieleck Q	q2 = 1
13	Strecke q3	Strecke[Q3, P3] von Vieleck Q	q3 = 12
13	Strecke p31	Strecke[P3, Q4] von Vieleck Q	p31 = 1
14	Gerade a	Gerade durch Q3, Q2	a: x = 12
15	Gerade d	Gerade durch P1, P2	d: x = 4
16	Gerade b	Gerade durch Q4, Q2	b: y = 3
17	Punkt A	Schnittpunkt von b, d	A = (4, 3)
18	Gerade c	Gerade durch P3, A	c: x + 4y = 16
19	Punkt B	Schnittpunkt von a, c	B = (12, 1)
20	Gerade e	Gerade durch B parallel zu xAchse	e: y = 1
21	Punkt C	Schnittpunkt von d, e	C = (4, 1)
22	Punkt D	Schnittpunkt von e, yAchse	D = (0, 1)
23	Punkt M	Mittelpunkt von C, P4	M = (4, -1.5)
24	Kreis k	Kreis mit Mittelpunkt M durch C	k: (x - 4)² + (y + 1.5)² = 6.25
25	Punkt E	Schnittpunkt von k, xAchse	E = (6, 0)
25	Punkt F	Schnittpunkt von k, xAchse	F = (2, 0)

Beschreibung des Vorgehens:

Wir zeichnen als Quadrat mit den Ecken . Dann zeichnen wir das Rechteck mit den Ecken und verwandeln dieses Rechteck mit dem Gnomonverfahren in ein flächengleiches Rechteck mit der Länge p. Das Differenzrechteck hat nun den Flächeninhalt . Um daraus die Wurzel zu ziehen, verwenden wir den Höhensatz. Wir zeichnen den Thaleskreis k über der Strecke mit und schneiden diesen Thaleskreis mit der x-Achse. Das gibt die Punkte und . Die x-Koordinaten der Punkte E und F sind die Lösungen der quadratischen Gleichung.

Das Verfahren funktioniert auch für negative p und/oder q.

3 Komplexe Lösungen

Für ergibt sich die quadratische Gleichung mit den beiden konjugiert komplexen Lösungen . Wie sieht das bei unseren grafischen Verfahren aus?

3.1 Die einfachste Methode

Der Kreis k schneidet die x-Achse nicht.

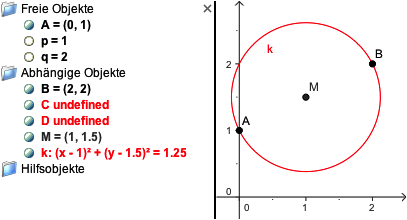
Keine reelle Lösung

Um das Problem zu Lösen, gehen wir in den Raum. Die x-Achse soll die bisherige Rolle weiterspielen, die y-Achse halten wir frei für die imaginäre Richtung, so dass die x,y-Ebene die Rolle der Gaußschen Zahlenebene übernimmt, und die z-Achse soll die Rolle der bisherigen y-Achse übernehmen. Das sieht dann zunächst so aus:

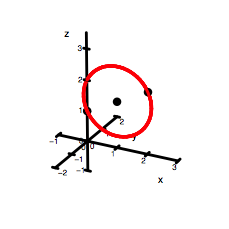
Im Raum

3.1.1 Zwischenspiel: Hyperboloid

Wenn wir in der Kugelgleichung ein Vorzeichen abändern, zum Beispiel zu , erhalten wir ein einschaliges Rotationshyperboloid mit gleichseitigen Hyperbeln als Profillinien. Der Kehlkreis (Breitenkreis mit kleinstem Umfang) hat in diesem Beispiel den Radius 1.

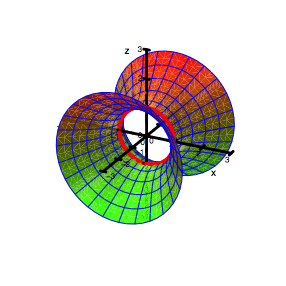
Rotationshyperboloid

Wir verwenden nun solche Hyperboloide zur Konstruktion der grafischen Lösungen der quadratischen Gleichung.

3.1.2 Beispiel

Im Beispiel verwenden wir den gezeichneten Kreis als Kehlkreis eines Hyperboloides. Dieses ist durch den Kehlkreis eindeutig festgelegt. Das Hyperboloid schneiden wir mit der x,y-Ebene, also mit der Gaußschen Ebene. Die Schnittfigur ist eine Hyperbel, deren Scheitel sind die Lösungen.

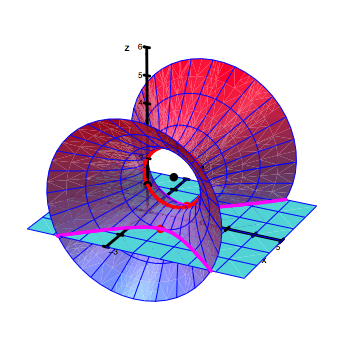
Schnitt mit der Gaußschen Zahlenebene

3.1.3 Allgemein

Dieses Verfahren funktioniert auch im reellen Fall. Die Hyperbel erscheint dann um 90° gedreht. Die Scheitel liegen auf der x-Achse.

Somit haben wir allgemein:

Wir zeichnen zunächst in der x,z-Ebene den Kehlkreis und dazu das Hyperboloid. Der schnitt mit der x,y-Ebene, also der Gaußschen Zahlenebene, ergibt eine Hyperbel. Deren Scheitelpunkt sind die Lösungen der quadratischen Gleichung.

Beweis:

Der Kehlkreis hat die Gleichungen:

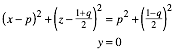
Das Hyperboloid hat daher die Gleichung:

Schnitt mit ergibt:

Dies lässt sich vereinfachen zu:

Das ist die Gleichung einer gleichseitigen Hyperbel in der x,y-Ebene.

Fallunterscheidung:

(I)

Die Hyperbel schneidet die x-Achse. Für erhalten und .

Die Figur illustriert den Fall . Es ist , sowie und .

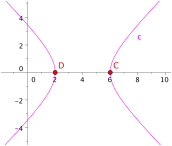
Hyperbel mit Scheitelpunkten

(II)

Die Hyperbel degeneriert zu zwei Geraden:

Die beiden Scheitel fallen zusammen und sind reell. Wir haben eine Doppellösung.

Die Figur illustriert den Fall . Es ist , sowie .

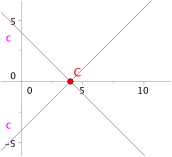
Doppellösung

(III)

Die Hyperbel hat die Scheitelpunkte auf der Symmetrieachse . Für ergibt sich

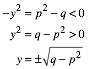
Die Scheitelpunkte haben also die Koordinaten ; es ist also und .

Die Figur illustriert den Fall . Die Hyperbel hat die Gleichung . Es ist .

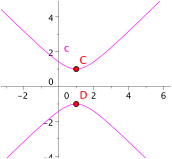
Komplexer Fall

3.2 Andere Methoden

In den Methoden Zweimalige Anwendung des Höhensatzes und Stur nach Formel kann völlig analog mit dem Hyperboloid gearbeitet werden.