Hans Walser, [20070407a], [20131218]
Quadratisches Rad
Anregung: T. U. – C. S.
1 Die Kettenlinie
Der
Funktionsgraph von ![]() wird als Kettenlinie bezeichnet, weil eine
durchhngende Kette diese Form annimmt.
wird als Kettenlinie bezeichnet, weil eine
durchhngende Kette diese Form annimmt.
Kettenlinie
Wir denken uns nun ein Lineal, das im Abstand 1 unterhalb der Oberkante einen Punkt P enthlt, und legen dieses Lineal so an den Scheitel S der Kettenlinie an, dass der Punkt P senkrecht unter den Scheitel S zu liegen kommt.
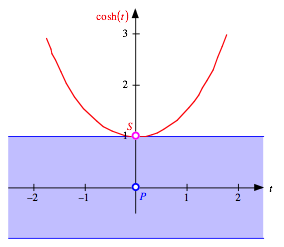
Anlegen des Lineals
Dann liegt der Punkt P natrlich im Ursprung.
Nun wlzen wir das Lineal auf der Kettenlinie ab und studieren die Bewegung des Punktes P.
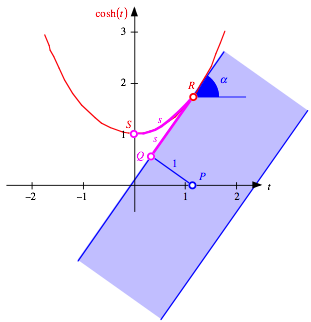
Abgewlztes Lineal
Die Figur suggeriert, dass P senkrecht unterhalb des Berhrungspunktes R auf der horizontalen Achse liegt. Dies ist auch richtig:
Der Punkt R habe die Darstellung:
![]()
Fr die abgewlzte Lnge s erhalten wir:
![]()
Fr den
Steigungswinkel ![]() gilt:
gilt:
![]()
Daraus ergibt sich:
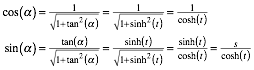
Somit hat der Punkt P die Darstellung:
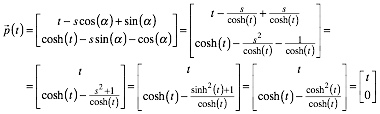
Damit liegt der Punkt P senkrecht unterhalb des Berhrungspunktes R auf der horizontalen Achse. Wir haben eine so genannte Geradfhrung.
2 Das quadratische Rad
Wir ersetzen den Streifen durch ein Quadrat der Seitenlnge 2 mit P als Mittelpunkt.
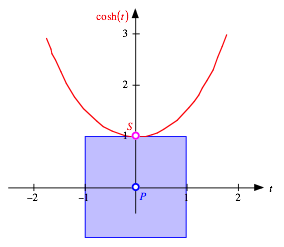
Quadratisches Rad
Dieses
knnen wir nun so lange abwlzen, bis die rechte obere Ecke auf der Kettenlinie
liegt. Dann ist ![]() . Fr den zugehrigen t-Wert
. Fr den zugehrigen t-Wert
![]() ergibt sich wegen
ergibt sich wegen
![]() :
:
![]()
An dieser Stelle setzen wir nun einen weiteren Kettelinienbogen an. Bei der nchsten Quadratecke verfahren wir wieder so. Damit erhalten wir eine Girlande von Kettenlinienbgen. Wenn wir schlie§lich noch an der horizontalen Achse spiegeln, ergibt sich eine Trasse, auf welchem das quadratische Rad vllig horizontal abrollen kann.
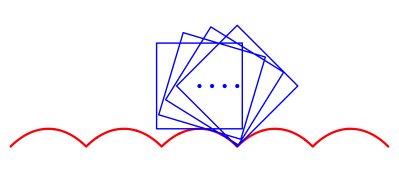
Trasse fr das quadratische Rad
Nach vier Umdrehungen ist das Rad wieder in gleicher Lage, weil der volle Umfang 8 abgewlzt worden ist. Damit ergibt sich die Periodenlnge p:
![]()
3 Das dreieckige Rad?
Analog
scheint es fr ein gleichseitiges Dreieck mit Innenkreisradius 1 zu funktionieren.
Die halbe Seitenlnge ist dann ![]() . Wir erhalten
. Wir erhalten
![]()
und die Periodenlnge p:
![]()
Die Trasse sieht so aus:
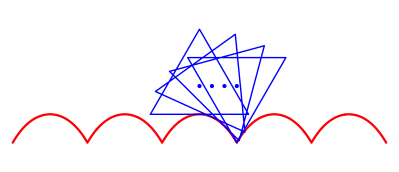
Trasse fr dreieckiges Rad?
Das funktioniert jetzt allerdings leider nicht. Eine Dreiecksecke nhert sich orthogonal der Trasse und hebt auch wieder orthogonal zur Trasse ab. In der Trasse habe wir aber dort einen Winkel von nur 60¡, so dass das Dreieck einhakt. Das folgende Bild zeigt die Situation stark vergr§ert.
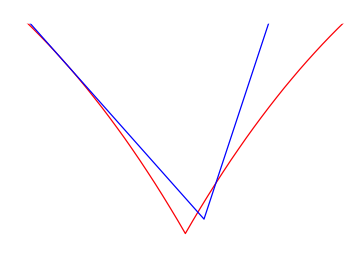
Dreieck hakt ein
4 Regelm§iges n-Eck
Allgemein
geht es aber fr ein regelm§iges n-Eck
mit ![]() und Innenkreisradius
1.
und Innenkreisradius
1.
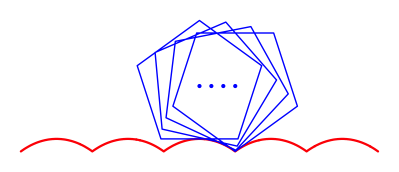
Regelm§iges Fnfeck
Die halbe
Seitenlnge dann ![]() . Weiter ist
. Weiter ist ![]() und fr die
Periodenlnge p ergibt sich
und fr die
Periodenlnge p ergibt sich ![]() .
.
5 Das Rad wird neu erfunden
Fr ![]() wird das Rad rund
und die Periodenlnge
wird das Rad rund
und die Periodenlnge ![]() . Es gilt daher:
. Es gilt daher:
![]()
Schauen wir das einmal an:
|
n |
n*arcsinh(tan(PI/n)) |
|
3 |
3.9508736908 |
|
4 |
3.5254943481 |
|
5 |
3.3713773881 |
|
6 |
3.2958368660 |
|
7 |
3.2526986741 |
|
8 |
3.2255977533 |
|
9 |
3.2074065425 |
|
10 |
3.1945825948 |
|
100 |
3.1421095524 |
|
1000 |
3.1415978213 |
|
10000 |
3.1415927053 |
|
100000 |
3.1415926541 |
Umwerfend
ist das allerdings nicht. Fr ![]() wird
wird ![]() klein und beide
beteiligten Funktionen knnen liniearisiert werden. Dann krzt sich das n heraus und es bleibt
klein und beide
beteiligten Funktionen knnen liniearisiert werden. Dann krzt sich das n heraus und es bleibt ![]() brig.
brig.