Hans Walser, [20130826]
Quadratrix
1 Die Kurve
Die Abbildung 1 zeigt die so genannte Quadratrix, die Kurve mit der Parameterdarstellung:
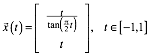
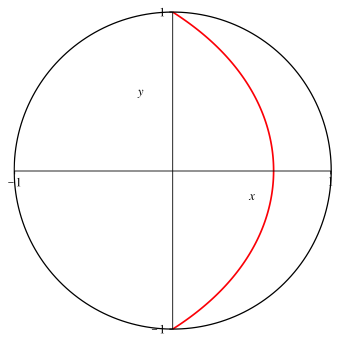
Abb. 1: Quadratrix
Die Quadratrix
schneidet die x-Achse bei 
und ist
daher fźr allerlei Spielereien im Bereich der Rektifikation oder der Quadratur
des Kreises geeignet.
†ber die Quadratrix siehe JŠger, Joachim und Schupp, Hans (2012).
2 Geradenscharen
Wir arbeiten nun mit
zwei Geradenscharen, nŠmlich einer Schar von parallelen Linien und einer Schar
von Ursprungsgeraden. Die parallelen Linien haben den Abstand 
und die
Ursprungsgeraden den Richtungsabstand 
. In der Abbildung 2 ist n = 4.
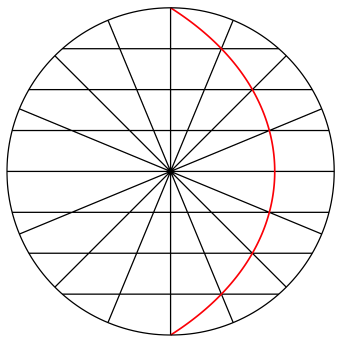
Abb. 2: Geradenscharen
Wir sehen, dass die Quadratrix durch geeignete Schnittpunkte verlŠuft.
Dies kann zur Winkeldrittelung verwendet werden. Der gelb markierte Winkel der Abbildung 3 kann gedrittelt werden, indem der horizontale hellblaue Streifen gedrittelt wird.
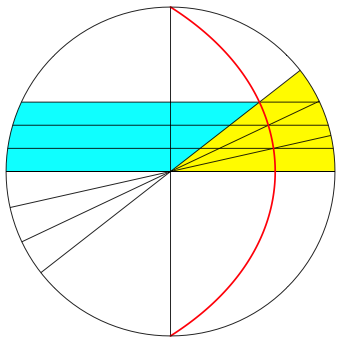
Abb. 3: Winkeldrittelung
3 Verdichtung und †berlagerung
Wir zeichnen nur die Geradenscharen mit sehr hoher Teilung (Abb. 4 und 5).
Abb. 4: Parallelen
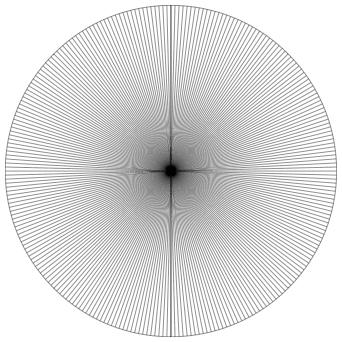
Abb. 5: Ursprungsgeraden
Leider sehen wir am Bildschirm in der Abbildung 5 einen MoirŽ-Effekt, der mir das Konzept versaut.
Nun źberlagern wir die Geradenscharen der Abbildungen 4 und 5. Wir erhalten einen MoirŽ-Effekt (Abb. 6). Leider haben wir auch hier einen durch die Bildschirmrasterung bedingten zusŠtzlichen MoirŽ-Effekt.
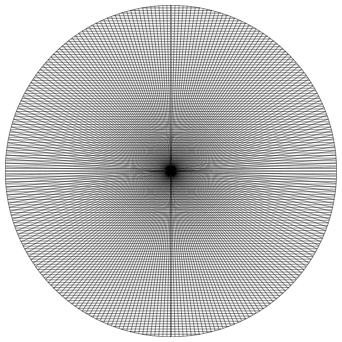
Abb. 6: MoirŽ-Effekt
Das ăLochŇ rechts in
der Abbildung 6 ist genau dort, wo die Quadratrix die Horizontale Gerade
schneidet, im Koordinatensystem der Abbildung 1 also im Punkt 
. Die Abbildung 7 illustriert die Situation.
Abb. 7: Mit Quadratrix
4 Benachbarte Kurven
Die Abbildung 8 zeigt eine Achterteilung der Geradenscharen und darin eingezeichnet die Quadratrix (rot) sowie auf beiden Seiten dazu Kurven (blau), welche durch benachbarte Schnittpunkte der Geradenscharen verlaufen.
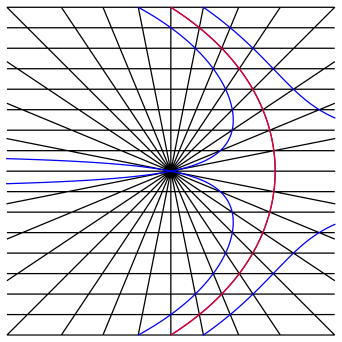
Abb. 8: Benachbarte Kurven
Die Abbildung 9 zeigt weitere benachbarte Kurven.
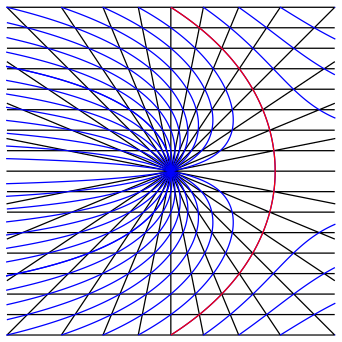
Abb. 9: Weitere benachbarte Kurven
Die Abbildung 10 zeigt zusŠtzlich die Konterschar, dafźr sind die ursprźnglichen Geradenscharen weggelassen. Die Quadratrix ist ebenfalls als Scharkurve gezeichnet.
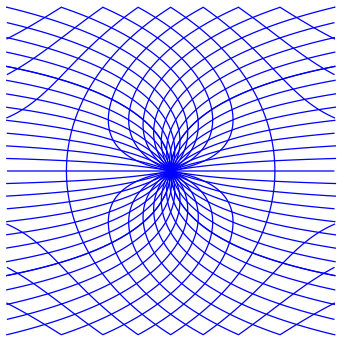
Abb. 100: Kurvenscharen
Literatur
JŠger, Joachim und Schupp, Hans (2012). Die Quadratrix: MU. Der Mathematikunterricht. Analysis – RatschlŠge und VorschlŠge 1. Herausgeber: Hans Schupp. Jahrgang 58.Heft 5.Oktober 2012.