1 Worum geht es?

Anordnungsspielerei mit natürlichen Zahlen. Der Autor sieht den Sinn auch nicht ein.

2 Aufbau der Spirale

Wir ordnen die natürlichen Zahlen, mit null beginnend, linear an, aber bei jeder Quadratzahl schlagen wir einen rechten Winkel nach links (Abb. 1 und 2).

Abb. 1: Anordnen der natürlichen Zahlen

Abb. 2: Zahlenspirale

3 Vier Spiralen

Dazwischen haben noch drei weitere Spiralen Platz (Abb. 3).

Abb. 3: Vier Spiralen

4 Markierungen

Wir können gewisse Zahlen markieren in der Hoffnung, ein Muster zu erkennen.

In der Abbildung 4 sind die Felder der ungeraden Zahlen gelb markiert. Das ergibt ein Streifenmuster.

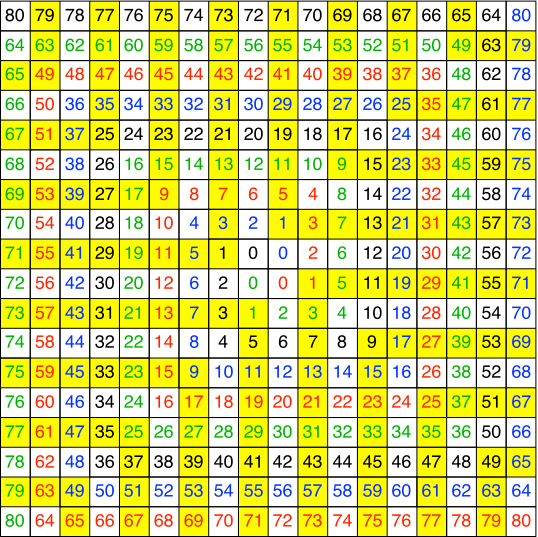
Abb. 4: Gerade / ungerade

Die Färbung modulo 3 gibt kein schönes Muster (Abb. 5).

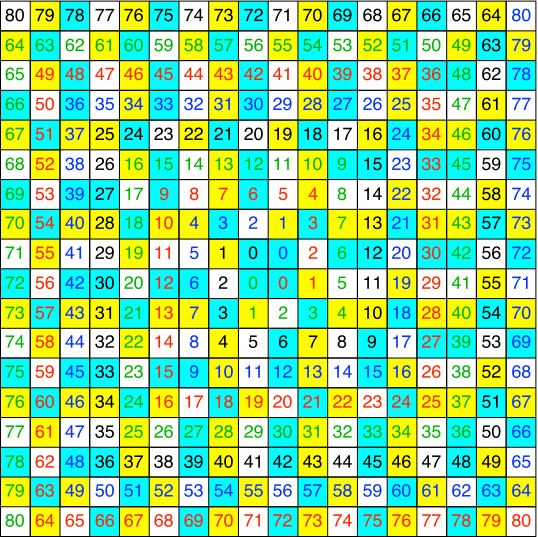
Abb. 5: Färbung modulo 3

Die Färbung modulo 4 führt zu einem Domino-Stein-Muster (Abb. 6 und 7).

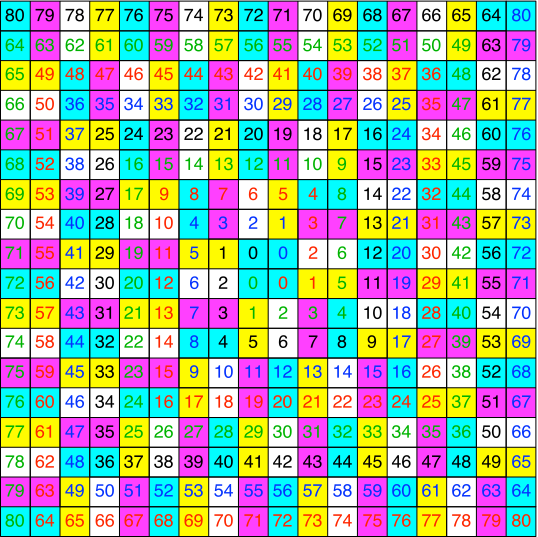
Abb. 6: Modulo 4

Abb. 7: Domino-Steine

In den Abbildungen 8 und 9 sind die Felder der Primzahlen gelb markiert.

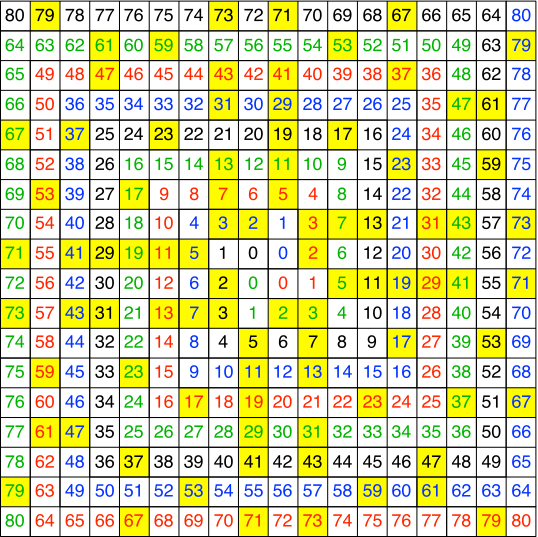
Abb. 8: Primzahlen

Abb. 9: Felder der Primzahlen

Bei weiterem Herauszoomen werden gewisse Muster erkennbar (Abb. 10 und 11 mit roter Markierung der Primzahlfelder).

Abb. 10: Rote Primzahlfelder

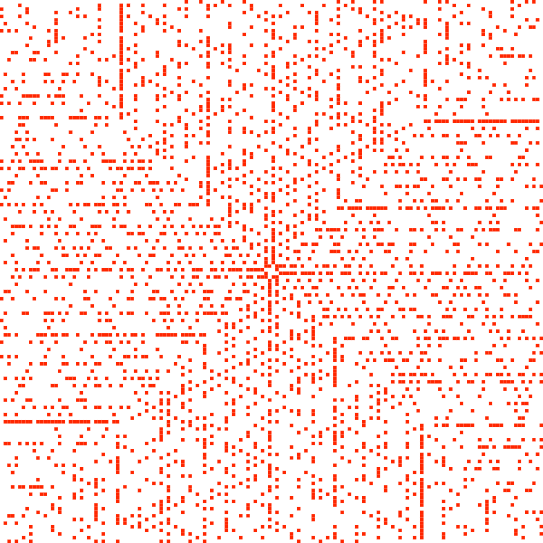
Abb. 11: Noch mehr Primzahlen

Literatur

Walser, Hans (2022): Spiralen, Schraubenlinien und spiralartige Figuren. Mathematische Spielereien in zwei und drei Dimensionen. Springer Spektrum. ISBN 978-3-662-65131-5 und ISBN 978-3-662-65132-2 (eBook).