Hans Walser, [20210122]

Quadratsummen

1 Erinnerung

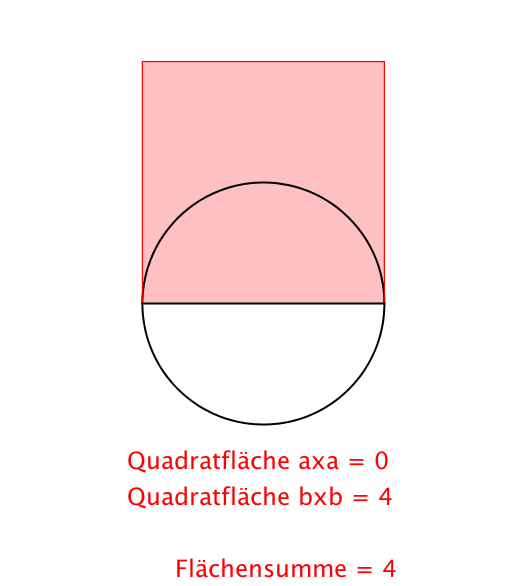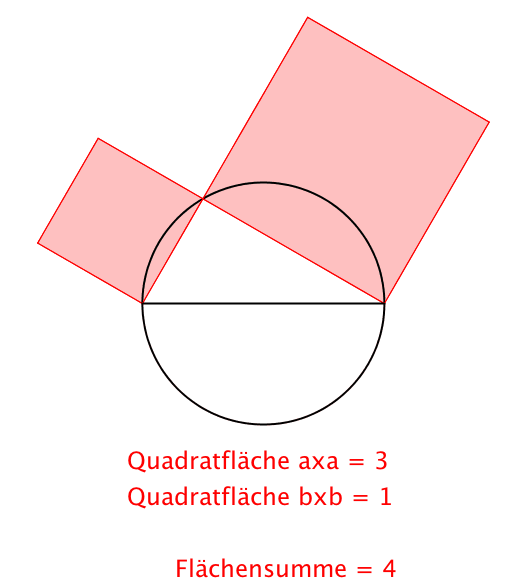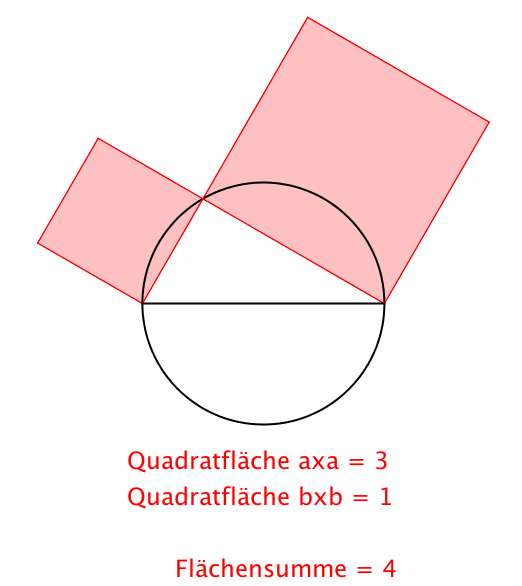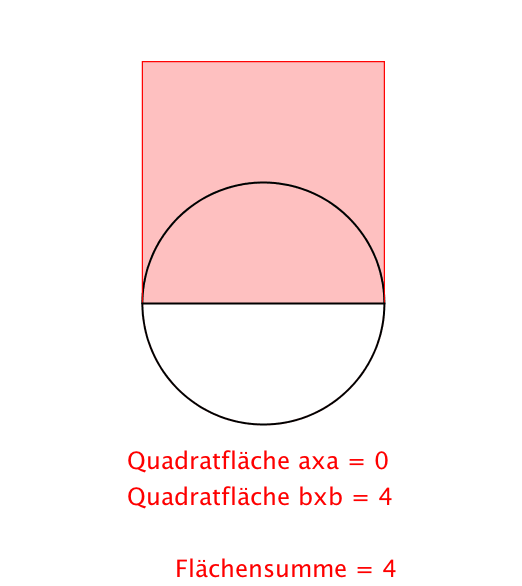
Abb. 1: Pythagoras

2 Kurvenfahrten

Abb. 2: Sinuskurve

Abb. 3: Als ich das erste Mal auf dem Dampfwagen saß

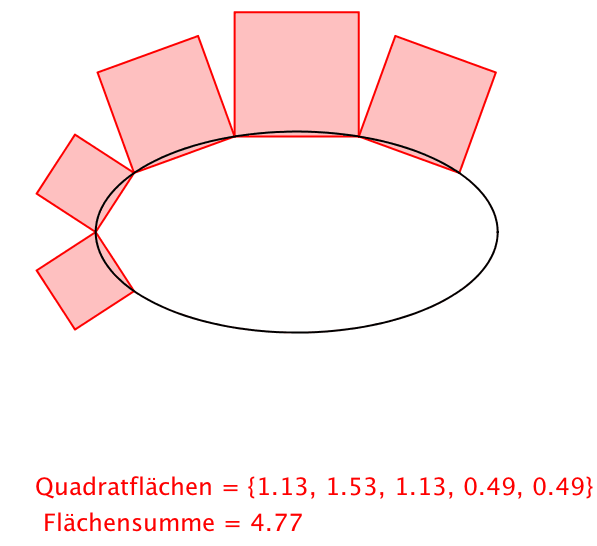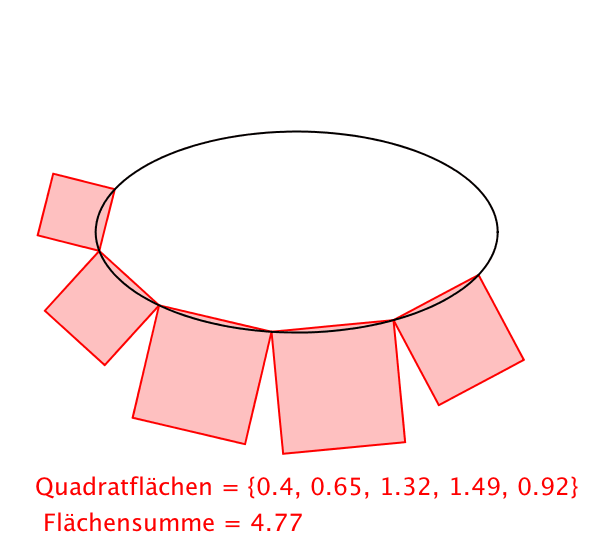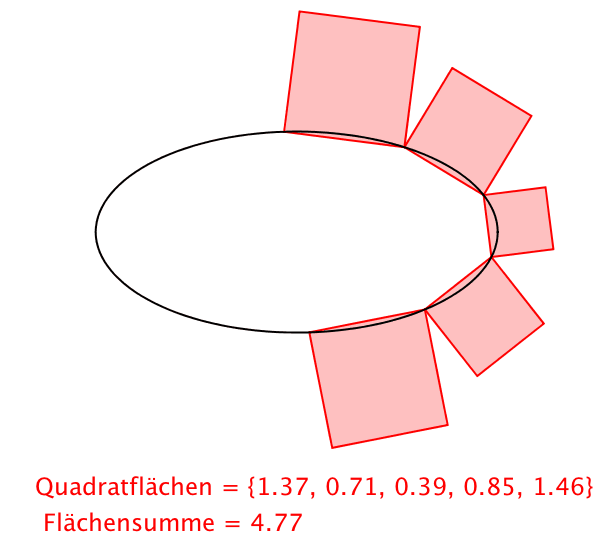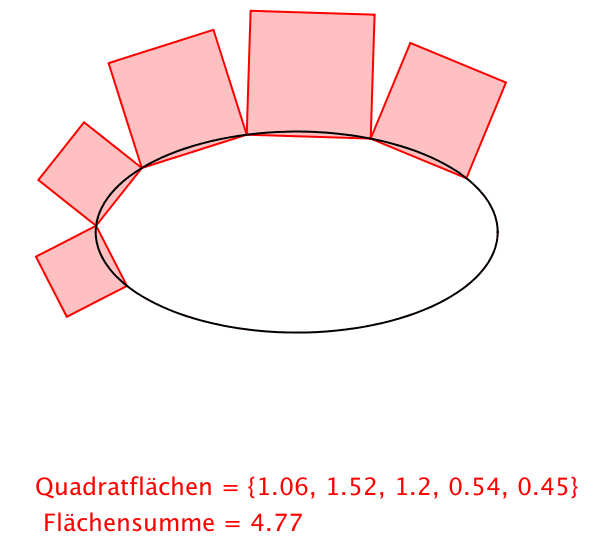
Abb. 4: Ellipse

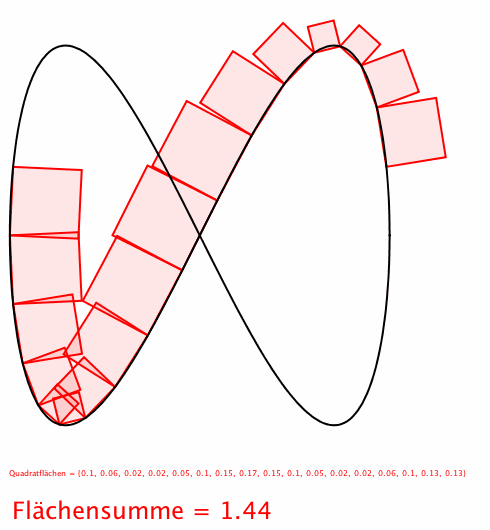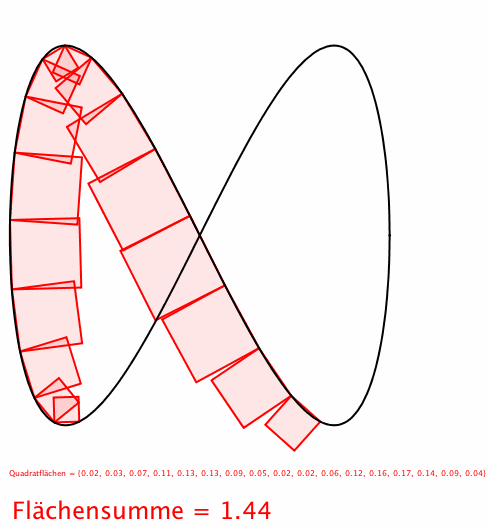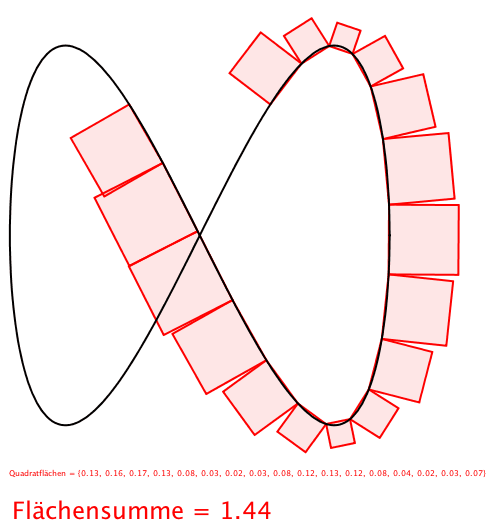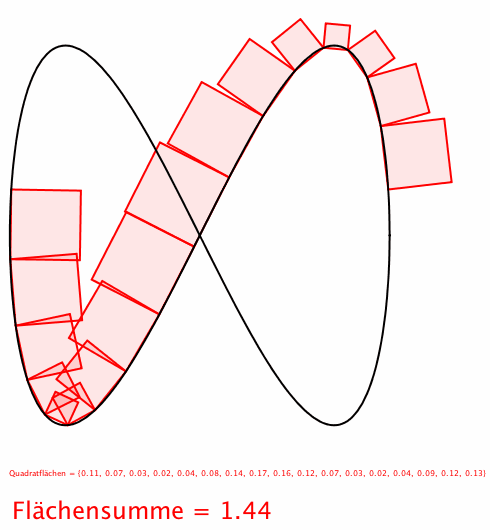
Abb. 5: Achterbahn

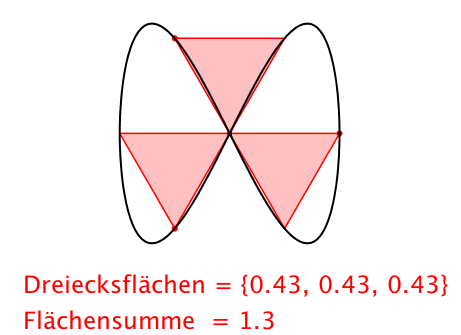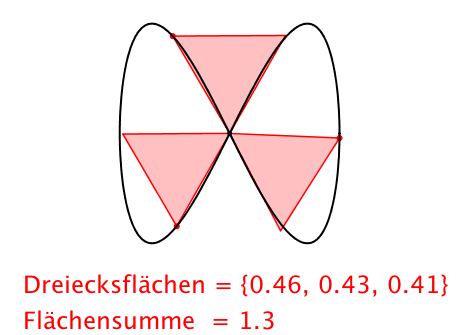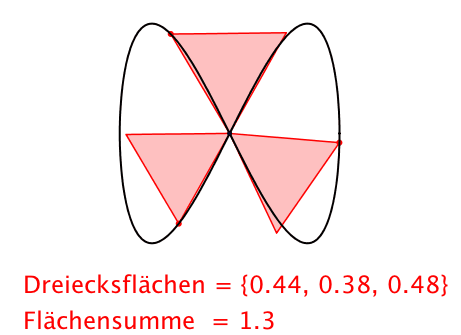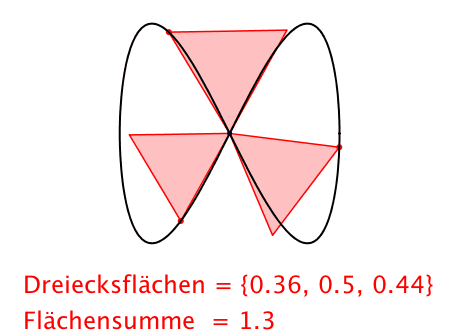
Abb. 6: Dreiecke

3 Externer Pivot

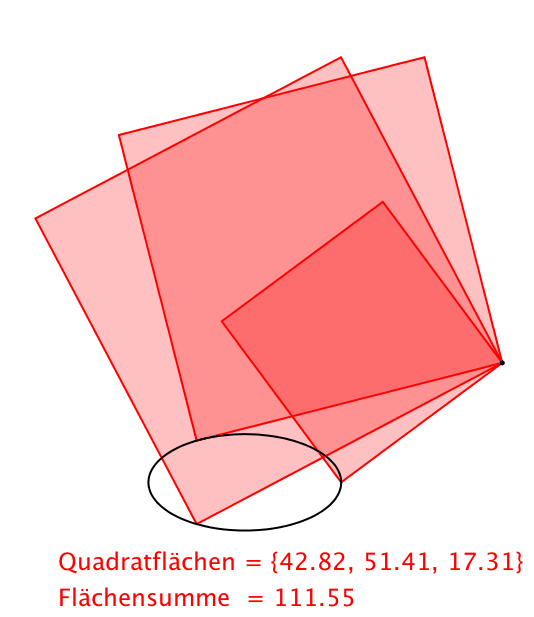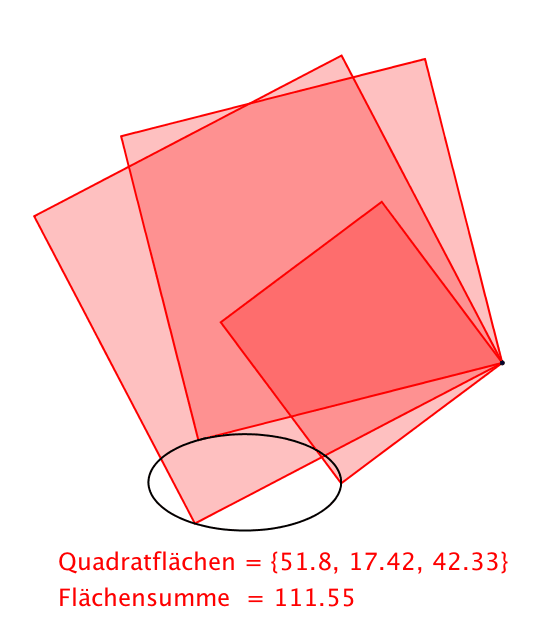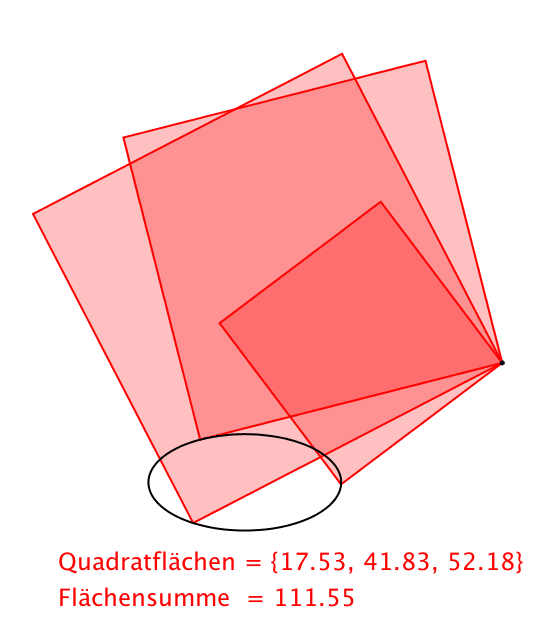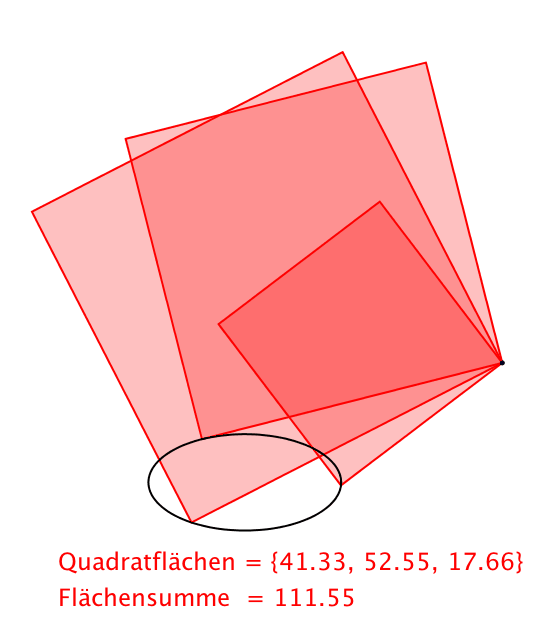
Abb. 7: Externer Pivot bei Ellipse

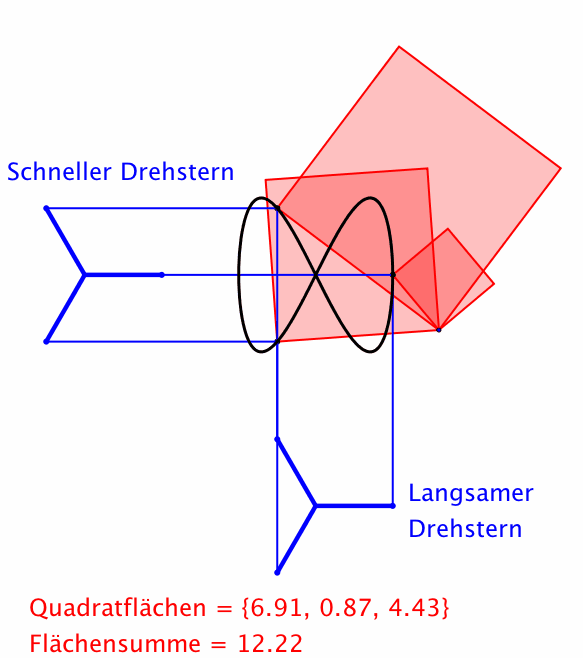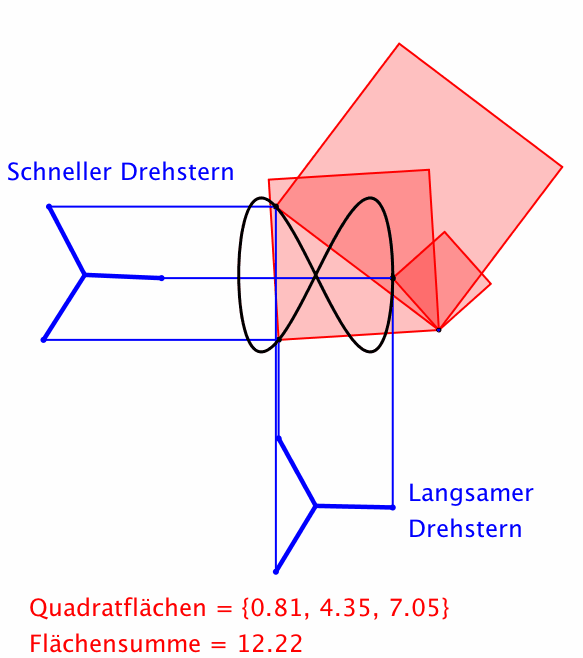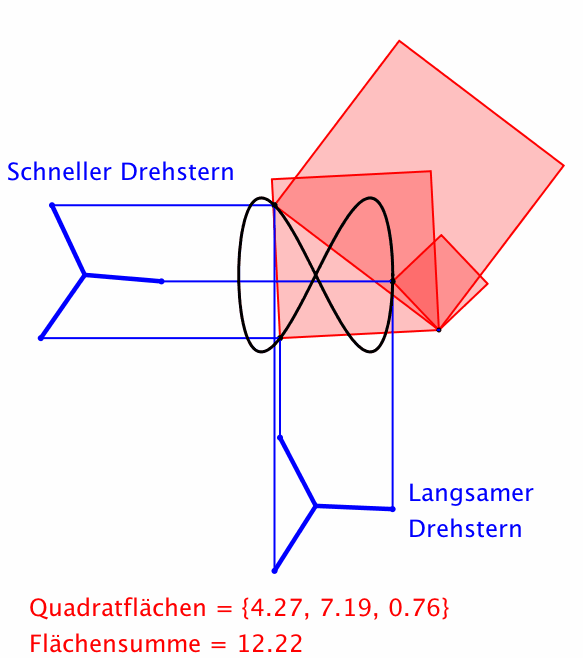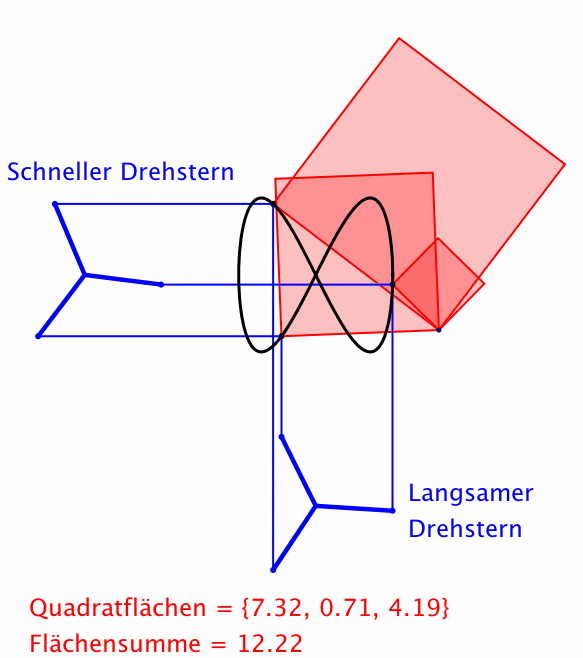
Abb. 8: Drehsterne

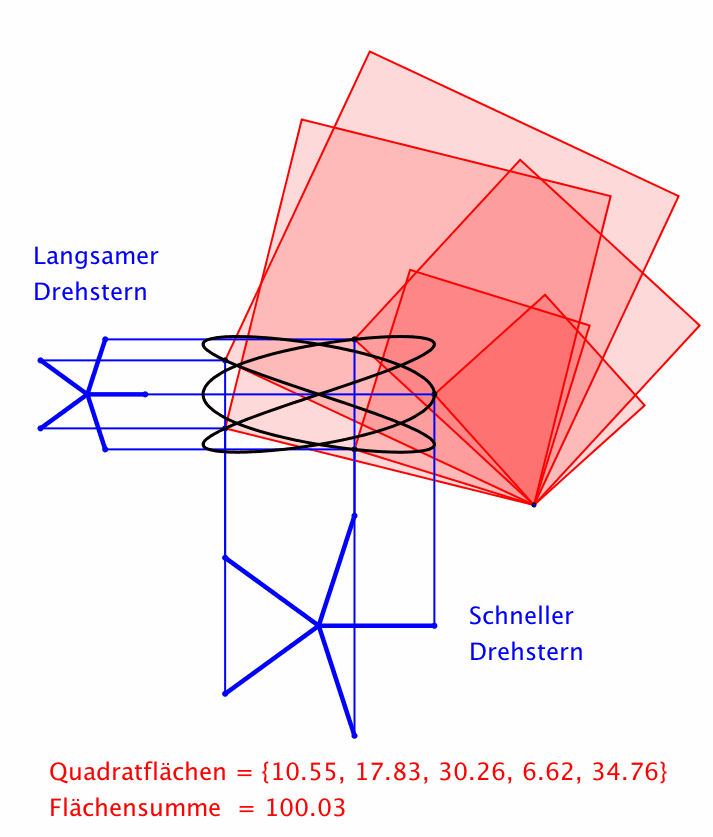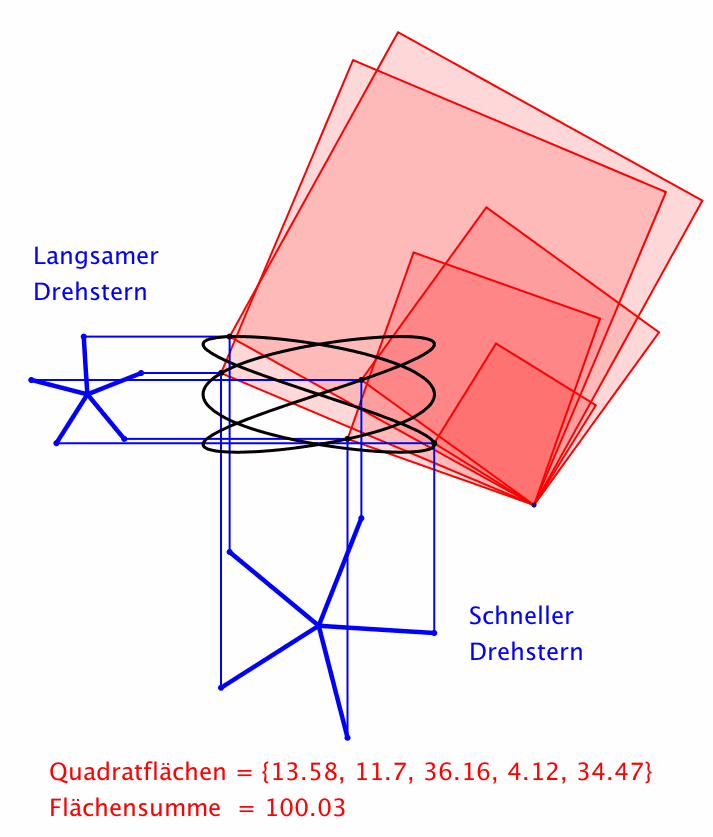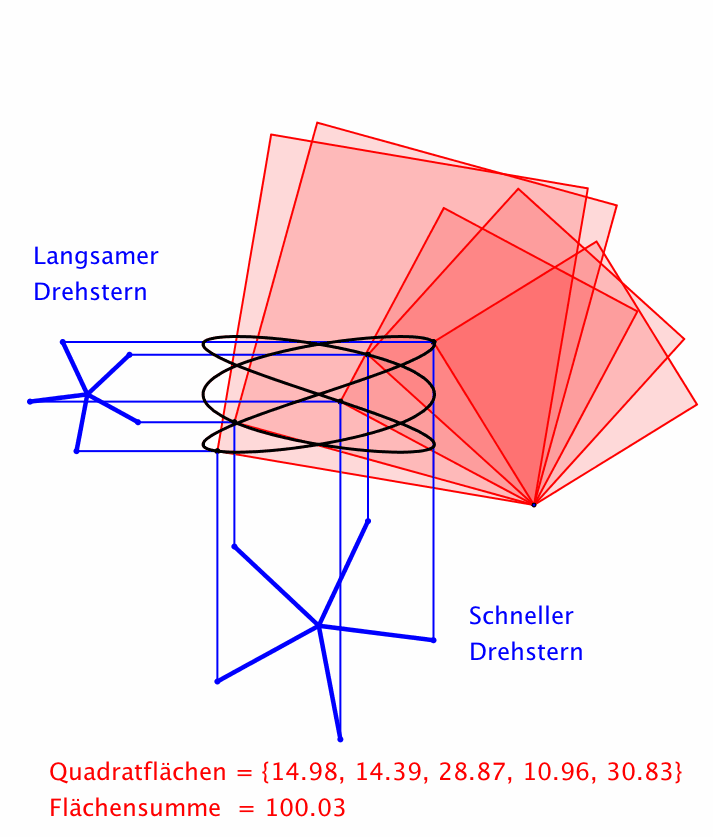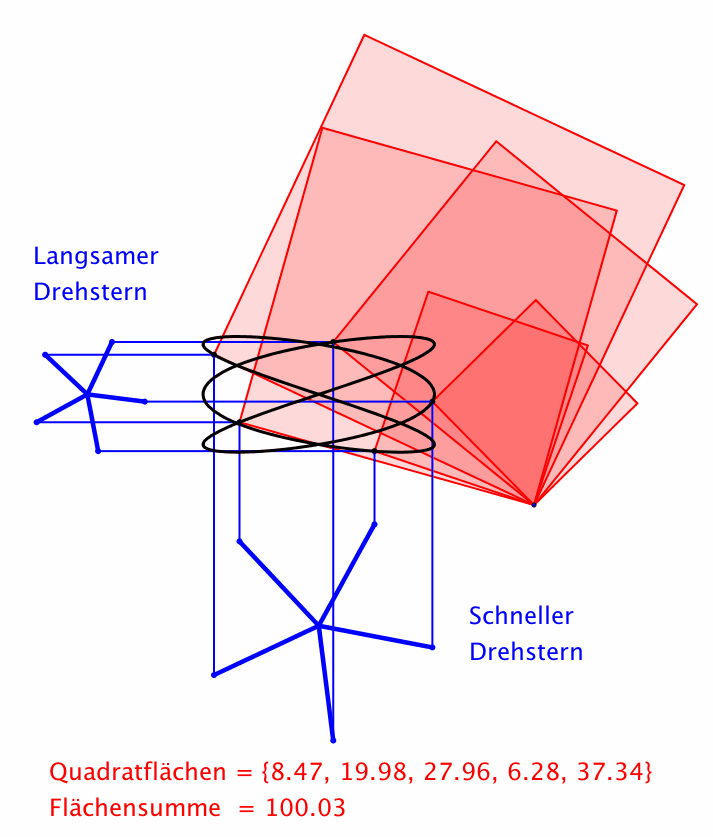
Abb. 9: Drehsterne

4 Beweise

4.1 Formeln

Wir benötigen die nachfolgenden Formeln.

4.1.1 Summe und Differenz von Winkeln

Aus den Additionstheoremen folgt:

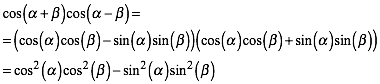(1)

Analog:

(2)

4.1.2 Zyklische Summen

Die zyklischen Summen sind hier für k = 1 ... n notiert. Wir können aber eben so gut die Summation für k = 0 ... n–1 oder allgemein für k = 1+m ... n+m laufen lassen, ohne dass sich am Resultat etwas ändert. Eine Runde ist eine Runde, egal wo sie gestartet wird.

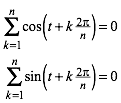(3)

Beweis: Die Vektoren

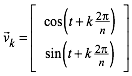(4)

lassen sich zu einem geschlossenen regelmäßigen n-Eck zusammenfügen (Abb. 5 für n = 5). Dabei ist t der Verdrehungswinkel der Figur. Auf das Resultat in (3) hat er keinen Einfluss. Hier tritt zum ersten Mal das Phänomen der Invarianz auf.

Abb. 10: Umordnen der Vektoren

Etwas allgemeiner:

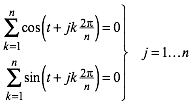(5)

Die Abbildung 6 deutet den Beweis für n = 5 und j = 2 an. Wie ist es, wenn j ein Teiler von n ist?

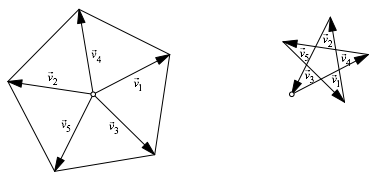
Abb. 11: Weihnachten kommt bestimmt

4.1.3 Zyklische Summen mit Quadraten

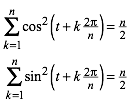(6)

Herleitung: Aus dem Additionstheorem für den Kosinus ergibt sich:

(7)

Daher ist:

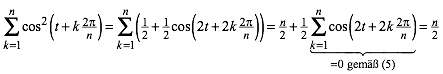(8)

Statt t fällt jetzt 2t heraus.

Damit ist die erste Zeile von (6) gezeigt. Da die Summe der beiden linken Seiten von (6) den Wert n ergibt, folgt die zweite Zeile von (6).

4.1.4 Zyklische Summe eines speziellen Produktes

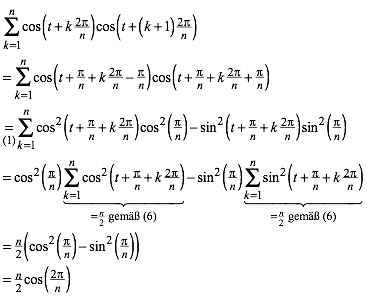(9)

Statt t fällt jetzt weg.

Analog zu (9) finden wir (merkwürdigerweise dasselbe Resultat):

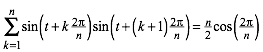(10)

4.2 Beweis für die Sinuskurve

Wir beweisen die Flächeninvarianz der Abbildungen 2 und 3. Es sei n die Anzahl der Quadrate und a die Amplitude der Sinuskurve. In beiden Abbildungen ist die horizontale Länge der Quadratfigur die halbe Periodenlänge, also π. Wegen der Schubspiegelsymmetrie der Sinuskurve können wir die Quadratsumme von 2n Quadraten, bezogen auf die horizontale Länge der vollen Periode, also 2π, berechnen (unser Formelapparat ist auf die volle Periodenlänge zugeschnitten), und dann das Resultat halbieren.

Es seien s_k, k = 1 ... 2n die Sehnenlängen in der Figur (Abb. 12) und damit die Seiten der Quadrate.

Abb. 12: Situation

Nach Pythagoras ist:

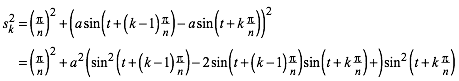(11)

Beim Aufsummieren verwenden wir (6) und (10) und erhalten:

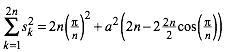(12)

Unsere Quadratflächensumme ist die Hälfte davon, also:

(13)

Da der Laufparameter t wegfällt (das geschieht in den zyklischen Summen) ist die Flächensumme invariant. Interessant ist das Auftreten von π².

4.3 Lissajous-Kurven und externer Pivot

Lissajous-Kurven sind Kurven mit der Parameterdarstellung:

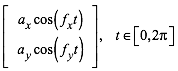(14)

Die Kurven der Abbildungen 4 bis 9 gehören dazu. Bei den Abbildungen 6 bis 9 haben wir einen externen Pivot mit den Koordinaten (p_x, p_y) (bei der Abbildung 6 ist der Kreuzungspunkt der „externe“ Pivot).

Für die Quadratseiten s_k, k = 1 ... n, erhalten wir:

(15)

Aufsummieren über k und Anwenden der einschlägigen Formeln liefert für die Summe der Quadratflächen (Abb.7 bis 9):

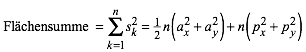(16)

Interessanterweise spielen die (allenfalls unterschiedlichen) Frequenzen f_x und f_y keine Rolle.

Bemerkung: (16) gilt nur, wenn die Frequenzen keine Vielfachen von n sind.

Bei der Abbildung 6 muss auf Dreiecksflächen umgerechnet werden.

4.4 Quadrate auf Lissajous-Kurven

Eine analoge Rechnung führt auf:

(17)

Hier spielen die Frequenzen eine Rolle.