Hans Walser, [20150440]
Quadratunterteilung
Anregung: Heinz Klaus Strick, Leverkusen
Die Abbildung 1 zeigt das unterteilte Quadrat.
Es ist eine infinite Unterteilung.
Wie gro§ sind die einzelnen Farbanteile?
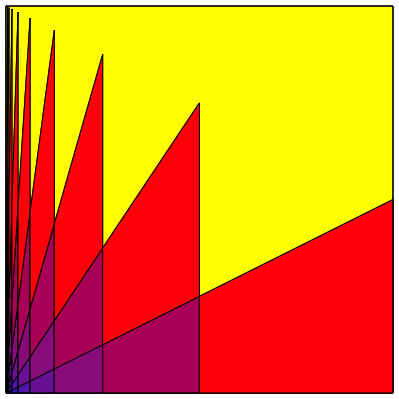
Abb. 1: Unterteiltes Quadrat
Mit Hilfe der Beziehung
lassen sich die Farbanteile rechnerisch bestimmen.
Es geht aber auch mit geometrischen †berlegungen.
In der Abbildung 2 ist ein schrŠger Streifen eingezeichnet. Der FlŠcheninhalt des Streifens ist die HŠlfte der QuadratflŠche. Innerhalb des Streifens gibt es zu jedem roten Dreieck ein flŠchengleiches gelbes Dreieck. Der rote und auch der gelbe FlŠchenanteil innerhalb des Streifens sind also je ein Viertel der QuadratflŠche.
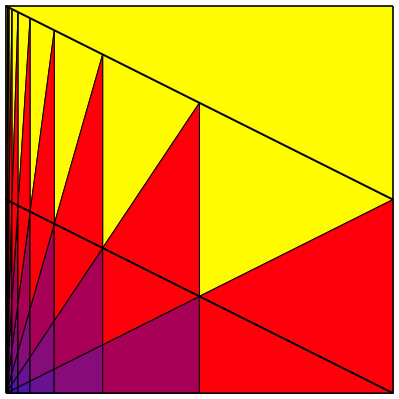
Abb. 2: SchrŠger Streifen
Das gelbe Dreieck oberhalb des Streifens hat auch einen Viertel der QuadratflŠche.
Somit ist der gelbe Anteil genau die HŠlfte der QuadratflŠche.
Der nicht gelbe Anteil macht also insgesamt die andere HŠlfte der QuadratflŠche aus.
Nun arbeiten wir mit dem Viertelquadrat links unten (Abb. 3). Dieses Viertelquadrat ist im Wesentlichen eine Kopie des Ausgangsquadrates.
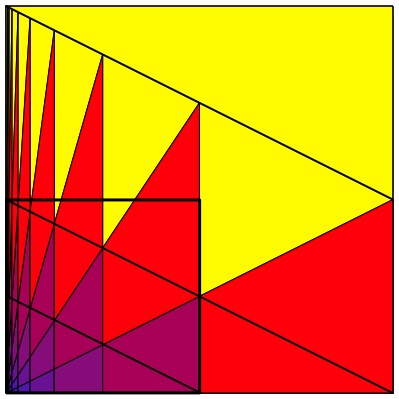
Abb. 3: Viertelquadrat
Im
schrŠgen Streifen in diesem Viertelquadrat macht der rote Anteil einen Viertel
der ViertelquadratflŠche aus also 
der
ursprŸnglichen QuadratflŠche. Das rote rechtwinklige Dreieck unten rechts ist
ebenfalls 
der
ursprŸnglichen QuadratflŠche. Somit erhalten wir fŸr den gesamten roten Anteil 
der
ursprŸnglichen QuadratflŠche.
Der
anschlie§ende magenta Anteil ist eine lŠngenmŠ§ig halbierte Kopie des roten Anteils
und daher flŠchenmŠ§ig 
der
ursprŸnglichen QuadratflŠche.
So geht das weiter.
Kontrolle
fŸr den nicht gelben Anteil: 