Hans Walser, [20170826]
Quadratunterteilung
1 Gleichm§ig wachsende Seitenlngen
Wir beginnen mit einer diagonal angeordneten Folge von Quadraten mit den Seitenlngen 1, 2, ... , 10. (Abb. 1).
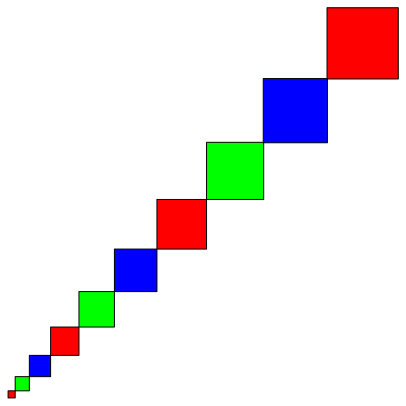
Abb. 1: Quadratfolge
Wir ergnzen die Figur zu einem gro§en Quadrat (Abb. 2). So entsteht ein Rechtecksraster.
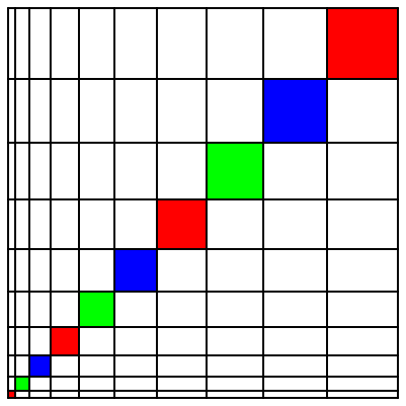
Abb. 2: Rechtecksraster
Zwischenbemerkung: In der Tabelle 1 sind die Flcheninhalte der Rechtecke in gleicher Anordnung wie in der Abbildung 2 eingetragen. Das haben wir schon einmal gesehen.
|
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
|
9 |
18 |
27 |
36 |
45 |
54 |
63 |
72 |
81 |
90 |
|
8 |
16 |
24 |
32 |
40 |
48 |
56 |
64 |
72 |
80 |
|
7 |
14 |
21 |
28 |
35 |
42 |
49 |
56 |
63 |
70 |
|
6 |
12 |
18 |
24 |
30 |
36 |
42 |
48 |
54 |
60 |
|
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
|
4 |
8 |
12 |
16 |
20 |
24 |
28 |
32 |
36 |
40 |
|
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
27 |
30 |
|
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Tab. 1: Flcheninhalte
In der Abbildung 3 ist eine Art ãDiagonaleÒ von links oben nach rechts unten eingetragen. Was fr eine Kurve ist das?
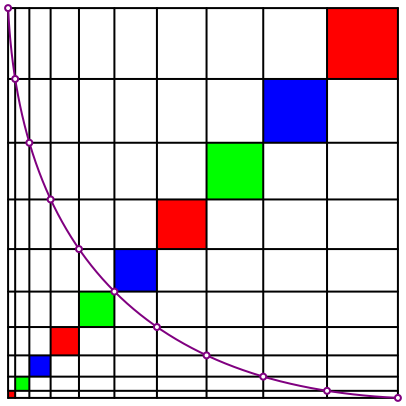
Abb. 3: Diagonale
Wir arbeiten zunchst im x,y-Koordinatensystem mit dem Ursprung in der linken unteren Ecke des gro§en Quadrates und der Seitenlnge des kleinsten roten Quadrates als Einheit. In diesem Koordinatensystem hat die Kurve die implizite Gleichung:
![]() (1)
(1)
Mit der Koordinatentransformation
![]() (2)
(2)
erhalten wir die Parabelgleichung:
![]() (3)
(3)
Nun unterteilen wir jedes Rechteck der Abbildung 2 in mglichst wenige Quadrate (Abb. 4).
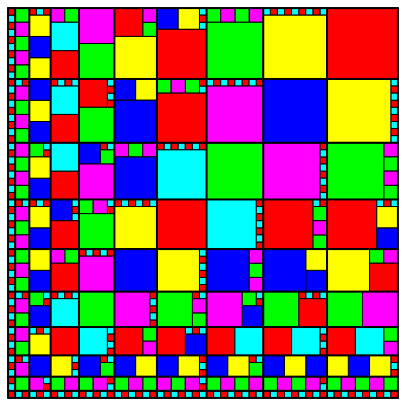
Abb. 4: Unterteilung in Quadrate
In der Tabelle 2 sind die Anzahlen der zur Unterteilung eines Rechtecks bentigten Quadrate eingetragen.
|
10 |
5 |
6 |
4 |
2 |
4 |
6 |
5 |
10 |
1 |
|
9 |
6 |
3 |
6 |
6 |
3 |
6 |
9 |
1 |
10 |
|
8 |
4 |
5 |
2 |
5 |
4 |
8 |
1 |
9 |
5 |
|
7 |
5 |
5 |
5 |
5 |
7 |
1 |
8 |
6 |
6 |
|
6 |
3 |
2 |
3 |
6 |
1 |
7 |
4 |
3 |
4 |
|
5 |
4 |
4 |
5 |
1 |
6 |
5 |
5 |
6 |
2 |
|
4 |
2 |
4 |
1 |
5 |
3 |
5 |
2 |
6 |
4 |
|
3 |
3 |
1 |
4 |
4 |
2 |
5 |
5 |
3 |
6 |
|
2 |
1 |
3 |
2 |
4 |
3 |
5 |
4 |
6 |
5 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Tab. 2: Anzahl der bentigten Quadrate zur Unterteilung
Lesebeispiel: Zur Unterteilung eines Rechteckes der Lnge 7 und der Hhe 4 bentigen wir 5 Quadrate (Abb. 5).

Abb. 5: Lesebeispiel
Berechnen tun wir das so:
 (4)
(4)
Dies ist zunchst der Euklidische Algorithmus zur Berechnung des gr§ten gemeinsamen Teilers der beiden Zahlen 7 und 4. Dieser gr§te gemeinsame Teiler ist der letzte von null verschiedene Rest, in unserem Falle 1. Uns interessiert das aber gar nicht. Wir addieren vielmehr die in (4) rot und blau angegebenen Zahlen. Diese Summe ist die Anzahl der bentigten Quadrate zur Unterteilung des Rechteckes der Lnge 7 und der Hhe 4. Der Zusammenhang mit der Abbildung 5 ist offensichtlich.
Die allgemeine Prozedur fr ein Rechteck der Lng m und der Hhe n sieht so aus:
AnzahlQuadrate:=proc(m,n)
local s,q,r,a,b,k:
s:=0:
q:=0:
r:=1:
a:=m:
b:=n:
for k from 0 while r > 0 do
q:=floor(a/b):
s:=s+q:
r:= a mod b:
a:=b:
b:=r:
end:
return s:
end:
Die Abbildung 6 gibt ein Histogramm fr die Tabelle 2.
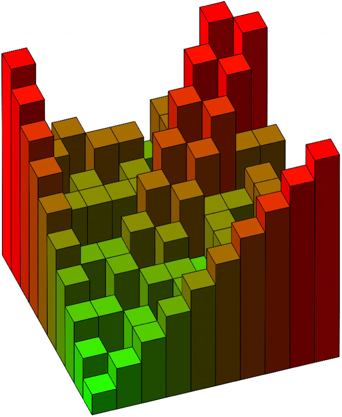
Abb. 6: Histogramm
Ein Zahlendreieck: Wir schreiben die obere linke Hlfte der Tabelle in einer anderen Anordnung und ergnzen am linken Rand mit Einsen (Tab. 3).
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
1 |
2 |
1 |
|
|
|
|
|
|
|
|
|
1 |
3 |
3 |
1 |
|
|
|
|
|
|
|
|
1 |
4 |
2 |
4 |
1 |
|
|
|
|
|
|
|
1 |
5 |
4 |
4 |
5 |
1 |
|
|
|
|
|
|
1 |
6 |
3 |
2 |
3 |
6 |
1 |
|
|
|
|
|
1 |
7 |
5 |
5 |
5 |
5 |
7 |
1 |
|
|
|
|
1 |
8 |
4 |
5 |
2 |
5 |
4 |
8 |
1 |
|
|
|
1 |
9 |
6 |
3 |
6 |
6 |
3 |
6 |
9 |
1 |
|
|
1 |
10 |
5 |
6 |
4 |
2 |
4 |
6 |
5 |
10 |
1 |
Tab. 3: Zahlendreieck
Es handelt sich hier um das Zahlendreieck A110570.
2 Fibonacci-Quadrate
Die Startquadrate haben die Fibonacci-Zahlen als Seitenlngen (Abb. 7).
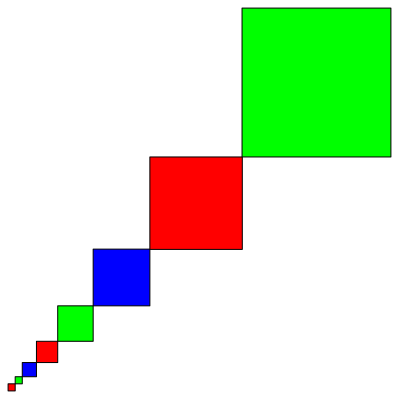
Abb. 7: Fibonacci-Quadrate
Die Fibonacci-Rekursion kann geometrisch gezeigt werden (Abb. 8).

Abb. 8: Fibonacci-Rekursion
Wir ergnzen die Abbildung 7 zum Rechtecksraster (Abb. 9).
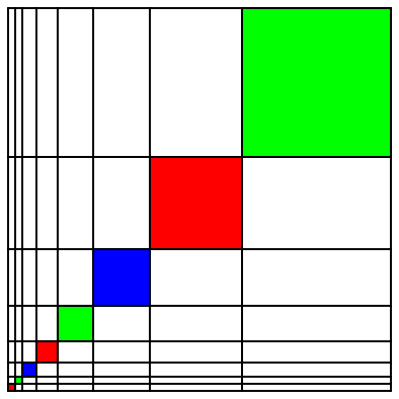
Abb. 9: Rechtecksraster
Die Tabelle 4 gibt die Flcheninhalte der einzelnen Rechtecke.
|
21 |
21 |
42 |
63 |
105 |
168 |
273 |
441 |
|
13 |
13 |
26 |
39 |
65 |
104 |
169 |
273 |
|
8 |
8 |
16 |
24 |
40 |
64 |
104 |
168 |
|
5 |
5 |
10 |
15 |
25 |
40 |
65 |
105 |
|
3 |
3 |
6 |
9 |
15 |
24 |
39 |
63 |
|
2 |
2 |
4 |
6 |
10 |
16 |
26 |
42 |
|
1 |
1 |
2 |
3 |
5 |
8 |
13 |
21 |
|
1 |
1 |
2 |
3 |
5 |
8 |
13 |
21 |
Tab. 4: Flcheninhalte
In der Abbildung 10 sind die Rechtecke in Quadrate zerlegt.
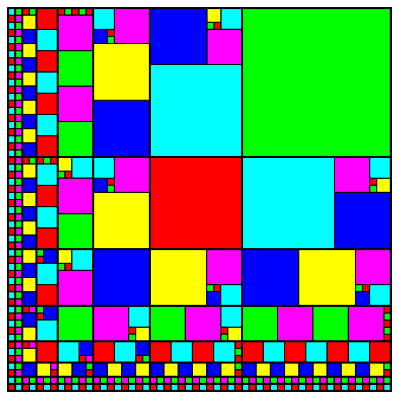
Abb. 10: Zerlegung in Quadrate
Die Tabelle 5 gibt die Anzahlen der fr die Zerlegung der einzelnen Rechtecke bentigten Quadrate.
|
21 |
21 |
12 |
7 |
9 |
7 |
7 |
1 |
|
13 |
13 |
8 |
7 |
6 |
6 |
1 |
7 |
|
8 |
8 |
4 |
5 |
5 |
1 |
6 |
7 |
|
5 |
5 |
4 |
4 |
1 |
5 |
6 |
9 |
|
3 |
3 |
3 |
1 |
4 |
5 |
7 |
7 |
|
2 |
2 |
1 |
3 |
4 |
4 |
8 |
12 |
|
1 |
1 |
2 |
3 |
5 |
8 |
13 |
21 |
|
1 |
1 |
2 |
3 |
5 |
8 |
13 |
21 |
Tab. 5: Anzahl der bentigten Quadrate zur Unterteilung
Websites
The On-Line Encyclopedia of Integer Sequences¨ (OEIS¨) (abgerufen 26.08.2017):