1 Worum es geht

Näherungskonstruktion für die Quadratur des Kreises. Die Konstruktion soll auf Leonardo da Vinci zurückgehen.

2 Problemstellung

Gesucht ist ein Quadrat mit demselben Flächeninhalt wie der Einheitskreis, also mit dem Flächeninhalt π.

3 Konstruktionsvorgang

In einem kartesischen Koordinatensystem zeichnen wir den Punkt A(0, 1) und die Gerade g mit der Gleichung y = 3x + 2√2 (Abb. 1).

Abb. 1: Punkt und Gerade

Weiter zeichnen wir den Kreis k mit dem Mittelpunkt A und dem Radius r = √2 – ⅕ (Abb. 2). Der Kreis k und die Gerade g haben zwei Schnittpunkte gemeinsam. Wir verwenden im Folgenden den unteren Schnittpunkt und bezeichnen ihn mit B.

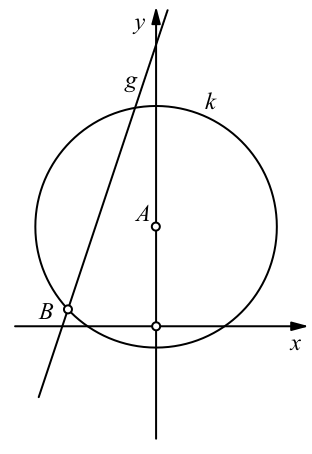
Abb. 2: Kreis. Schnittpunkt

Wir spiegeln den Punkt B an der y-Achse, den Bildpunkt bezeichnen wir mit C (Abb. 3).

Abb. 3: Spiegelpunkt

Die Punkt B und C sind die Stützpunkte des gesuchten Quadrates (Abb. 4).

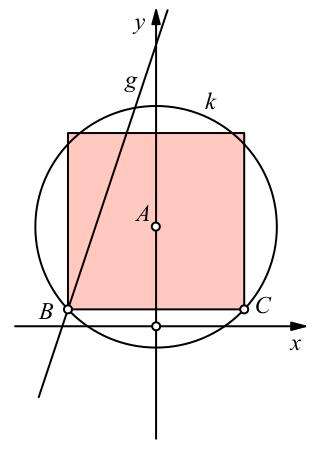
Abb. 4: Quadrat

In der Abbildung 5 ist zusätzlich der Einheitskreis e eingezeichnet.

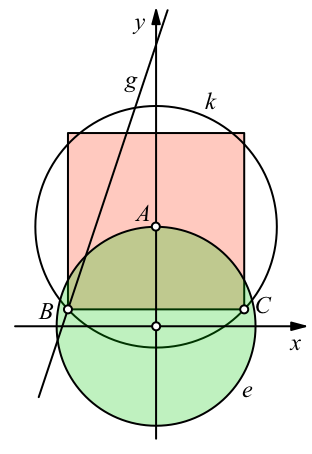
Abb. 5: Einheitskreis

4 Genauigkeit

Das rote Quadrat (Abb. 4) hat den Flächeninhalt ≈ 3.14117. Im Vergleich dazu hat der grüne Einheitskreis den Flächeninhalt π ≈ 3.14159. Das rote Quadrat ist also etwas zu klein.

5 Verändern des Radius

Der Kreis k hat den Radius r = √2 – ⅕ ≈ 1.214213562373095

Wenn wir diesen Radius vergrößern auf r ≈ 1.214380207930221, ergibt sich für den Flächeninhalt des roten Quadrates ≈ 3.141592653589792.

Im Vergleich dazu ist π ≈ 3.141592653589793. Die letzte Stelle stimmt nicht, dürfte aber ein Rundungsproblem des Computers sein.

Der vergrößerte Radius kann in der Form r ≈ √2 – 0.199833354442874 geschrieben werden. Statt ⅕ = 0.2 muss nur 0.199833354442874 subtrahiert werden.