Hans Walser, [20170916]

Quadratur des Rechtecks

1     Worum geht es

Durch einen iterierten FlŠchenverdoppelungsprozess nŠhert sich ein Rechteck einem Quadrat an.

2     Erinnerung

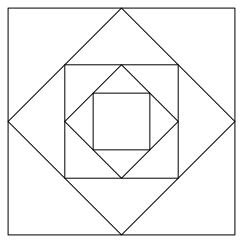
Abb. 1: Erinnerung

3     Verdoppelungsschritt im Rechteck

Wir umschreiben dem Rechteck ein zweites Rechteck, dessen Seiten parallel beziehungsweise orthogonal zu einer Diagonale des Ausgangsrechtecks sind (Abb. 2).

Abb. 2: Das neue Rechteck

Dabei wird der FlŠcheninhalt verdoppelt, wie die Zerlegung der Abbildung 3 zeigt.

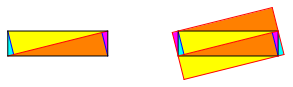
Abb. 3: FlŠchenverdoppelung

4     Iteration

Wir iterieren den Verdoppelungsschritt.

Die Abbildung 4 zeigt nochmals das Ergebnis des ersten Schrittes.

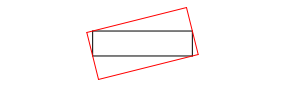
Abb. 4: Erster Schritt

Die Abbildungen 5 bis 8 zeigen die folgenden Schritte.

Abb. 5: Zweiter Schritt

Abb. 6: Dritter Schritt

Abb. 7: Vierter Schritt

Abb. 8: Fźnfter Schritt

Wir sehen, dass sich die Rechtecke immer mehr einem Quadrat annŠhern.

5     Beweis

5.1    Iterationsgleichungen

Wir verwenden fźr den Iterationsschritt die Bezeichnungen der Abbildung 9. Dabei soll  sein.

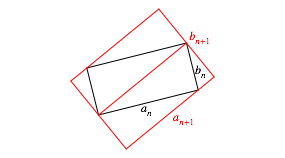
Abb. 9: Bezeichnungen

Damit erhalten wir die Iterationsgleichungen:

 

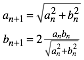                                                                                                             (1)

 

 

 

Im rechtwinkligen Dreieck ist die halbe Hypotenuse grš§er oder gleich der zur Hypotenuse gehšrenden Hšhe. Daher ist .

Weiter bezeichnen wir mit  das SeitenverhŠltnis im Rechteck:

 

                                                                                                                           (2)

 

 

Wir haben zu zeigen:

 

                                                                                                                      (3)

 

 

5.2    Iteration des SeitenverhŠltnisses

Aus (2) folgt  und damit:

 

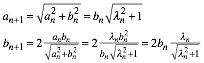                                                                     (4)

 

 

 

Fźr das neue SeitenverhŠltnis erhalten wir:

 

                                                               (5)

 

 

 

In unserem Beispiel der Abbildungen 2 bis 8 ist der Startwert . Damit erhalten wir die Werte der Tabelle 1.

 

n

0

4

1

2.125000000

2

1.297794118

3

1.034166181

4

1.000564381

5

1.000000159

Tab. 1: SeitenverhŠltnisse

In unserem Beispiel konvergieren die SeitenverhŠltnisse sehr rasch gegen 1.

Gilt das auch allgemein?

Wir besprechen zwei Vorgehensweisen.

5.2.1   Fixpunktverfahren

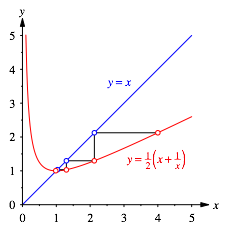
Abb. 10

Die Abbildung 10 illustriert die Situation mit dem Fixpunktverfahren. Der Punkt (1,1) ist ein attraktiver Fixpunkt. Bei einem beliebigen Startwert geht es treppab zu diesem Punkt. Daher ist der gesuchte Limes 1.

5.2.2   Heron und Newton-Raphson

Die positive Nullstelle der Funktion

 

                                                                                                             (6)

 

 

ist die Quadratwurzel aus r. Nach dem Verfahren von Newton-Raphson erhalten wir die Iteration:

 

                                                                   (7)

 

 

Mit einem beliebigen Startwert kšnnen wir damit die Quadratwurzel aus r approximieren. Das Verfahren wird auch als Verfahren von Heron bezeichnet.

Wir sehen, dass (5) der Sonderfall fźr r = 1 von (7) darstellt.

Der gesuchte Limes ist also die Quadratwurzel aus 1, somit 1.