Hans Walser, [20211229]
Quadratvergleich
1 Konstruktion
In ein Rechteck der Breite 1 und der Höhe h zeichnen wir den Kantenmittenrhombus. In die obere und untere Hälfte des Rhombus passen wir je ein Quadrat ein gemäß Abbildung 1.
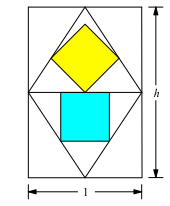
Abb. 1: Konstruktion
Die beiden Quadrate sind im Allgemeinen nicht flächengleich. Mit v(h) bezeichnen wir das Flächenverhältnis des gelben Quadrates zum hellblauen Quadrat. Im gezeichneten Beispiel (Abb. 1) ist:
![]() (1)
(1)
Das gelbe Quadrat ist in diesem Beispiel etwas kleiner als das hellblaue Quadrat.
2 Formel
Für das Flächenverhältnis v(h) ergibt sich mit etwas Rechnung:
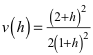 (2)
(2)
Die Abbildung 2 zeigt den Funktionsgrafen.
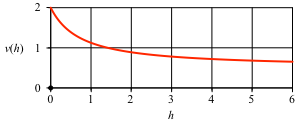
Abb. 2: Funktionsgraf
3 Diskussion
3.1 Flächengleiche Quadrate
Für v(h) = 1 sind die beiden Quadrate flächengleich. Dies führt auf:
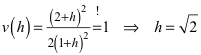 (3)
(3)
Die beiden Quadratflächen sind also bei einem Rechteck im DIN-Format (Walser 2013) gleich groß (Abb. 3).
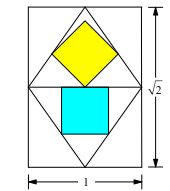
Abb. 3: Flächengleiche Quadrate beim DIN-Format
3.2 Unendlich hohes Rechteck
Für wachsendes h hat v(h) den Grenzwert ½. Aus dem Rechteck und dem Rhombus wird je ein senkrechter Streifen (Abb. 4). Das gelbe Quadrat ist flächenmäßig noch halb so groß wie das hellblaue.

Abb. 4: Senkrechter Streifen
3.3 Rechteck mit kleiner Höhe
Für h < 1 wird das gelbe Quadrat gemäß Abbildung 5 (h = 0.3) eingepasst.
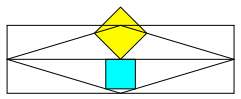
Abb. 5: Kleine Höhe
Gemäß (2) strebt v(h) gegen 2, wenn h gegen 0 strebt. Die Abbildung 6 zeigt nun den zentralen Ausschnitt für eine sehr kleine Höhe h (nämlich h = 0.01). Das gelbe Quadrat ist nun schon beinahe doppelt so groß wie das hellblaue. Es ist:
![]() (4)
(4)
Die Leserin oder der Leser hat natürlich gleich bemerkt, dass der Zähler in (4) eine Quadratzahl ist, nämlich das Quadrat von 201.

Abb. 6: Sehr kleine Höhe
3.4 Rationale Flächenverhältnisse
Für eine rationale Höhe h ist wegen (2) auch das Flächenverhältnis v(h) rational. Allerdings können auch irrationale Höhen zu einem rationalen Flächenverhältnis führen, wie das Beispiel (3) zeigt.
Wir setzen h= p/q mit teilerfremden p und q (also „optimal gekürzt“). Damit wird zunächst:
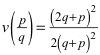 (5)
(5)
Wenn nun p gerade ist, kann in (5) noch weiter gekürzt werden. Es gilt:
 (6)
(6)
Durch Erweitern mit 2 können die Eigenschaften „Quadratzahl“ und „doppelte Quadratzahl“ vertauscht werden:
![]() (7)
(7)
4 Beispiele
Im Folgenden einige Beispiele mit rationalen Höhen. Das rationale Flächenverhältnis kann jeweils durch ein Puzzle illustriert werden.
4.1 Höhe gleich ein Drittel
Es ist:
![]() (8)
(8)
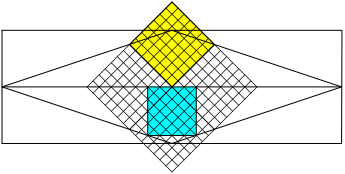
Abb. 7: Höhe gleich ein Drittel
Der Zähler in (8) ist eine Quadratzahl. Wir unterteilen nun das gelbe Quadrat in 7 mal 7 kleine Rasterquadrate, also 49 Rasterquadrate. Diese Rasterung setzen wir fort, bis sie das hellblaue Quadrat überdeckt. In diesem Quadrat haben wir nun 24 ganze Rasterquadrate und 16 halbe Rasterquadrate, also insgesamt 32 Rasterquadrate. Damit ist (8) erfüllt.
4.2 Höhe gleich ein Halbes
Es ist:
![]() (9)
(9)
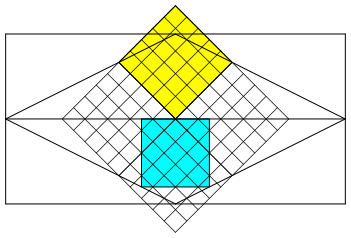
Abb. 8: Höhe gleich ein Halbes
Der Zähler in (9) ist wiederum eine Quadratzahl. Wir unterteilen entsprechend das gelbe Quadrat in 5 mal 5 kleine Rasterquadrate. Diese Rasterung setzen wir fort, bis sie das hellblaue Quadrat überdeckt. In diesem Quadrat haben wir nun 13 ganze Rasterquadrate, 8 halbe Rasterquadrate und 4 Viertel-Rasterquadrate, also insgesamt 18 Rasterquadrate. Damit ist (9) erfüllt.
4.3 Höhe gleich zwei Drittel
Es ist:
![]() (10)
(10)
Nun ist der Nenner eine Quadratzahl.
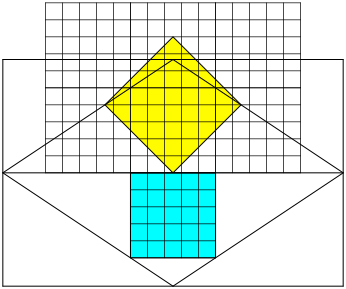
Abb. 9: Höhe gleich zwei Drittel
Wir unterteilen das hellblaue Quadrat in 5 mal 5 kleine Rasterquadrate und setzen die Rasterung fort, bis die das gelbe Quadrat überdeckt (Abb. 9). Und nun fängt im gelben Quadrat ein mühsames Auszählen der Rasterquadrate an (Abb. 10).
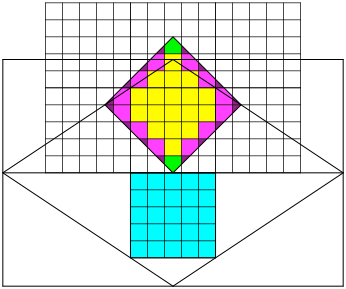
Abb. 10: Auszählen
Wir haben:
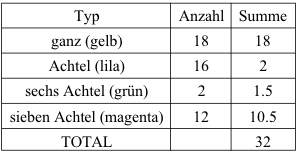 (11)
(11)
Wir können die Sache vereinfachen, indem wir mit 2 erweitern:
![]() (12)
(12)
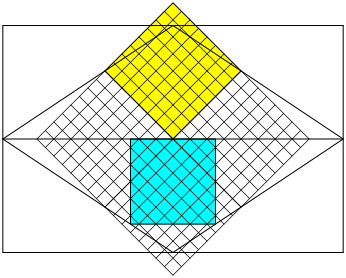
Abb. 11: Vereinfachung durch Erweitern
Der Zähler in (12) ist nun wiederum eine Quadratzahl. Wir unterteilen entsprechend das gelbe Quadrat in 8 mal 8 kleine Rasterquadrate. Diese Rasterung setzen wir fort, bis sie das hellblaue Quadrat überdeckt. In diesem Quadrat haben wir nun 41 ganze Rasterquadrate, 16 halbe Rasterquadrate und 4 Viertel-Rasterquadrate, also insgesamt 50 Rasterquadrate. Damit ist (12) erfüllt.
4.4 Höhe gleich eins
Das Startrechteck ist nun ein Quadrat. Es ist:
![]() (13)
(13)
Die Abbildung 12 zeigt das übliche Spielchen.

Abb. 12: Im Quadrat
4.5 Höhe gleich zwei
Es ist (mit Erweitern):
![]() (14)
(14)
Das hellblaue Quadrat ist nun größer als das gelbe (Abb. 13).

Abb. 13: Höhe gleich zwei
4.6 Höhe gleich drei
Es ist:
![]() (15)
(15)

Abb. 14: Höhe gleich drei
5 Eine Funktionalgleichung
Bei unseren Beispielen fällt folgendes auf:
![]() (16)
(16)
Und:
![]() (17)
(17)
Die Frage ist, für welche Werte von h wir jeweils Kehrwerte der Flächenverhältnisse v(h) finden.
Mit einigem Probieren finden wir:
![]() (18)
(18)
Der doppelte Kehrwert von h führt zum Kehrwert des Flächenverhältnisses v(h). Diese Funktionalgleichung kann mit (2) nachgewiesen werden.
Websites
Hans Walser: Quadrat im Dreieck
http://www.walser-h-m.ch/hans/Miniaturen/Q/Quadrat_im_Dreieck/Quadrat_im_Dreieck.htm
Hans Walser: Quadratgleichheit
http://www.walser-h-m.ch/hans/Miniaturen/Q/Quadratgleichheit/Quadratgleichheit.html
Literatur
Walser, Hans (2013): DIN A4 in Raum und Zeit. Silbernes Rechteck – Goldenes Trapez – DIN-Quader. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-69-1.