Hans Walser, [20200818]
Quersummen
1 Worum geht es?
Quersummen in der Darstellung mit der Basis b.
2 Geometrischer Einstieg
Basis b = 2.
Wir beginnen mit einem Kreis im Ursprung eines kartesischen Koordinatensystems (Abb. 1.0).
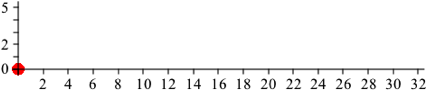
Abb. 1.0: Kreis im Ursprung
Wir verschieben eine Kopie dieses Kreises um eine Einheit nach rechts und um eine Einheit nach oben (Abb. 1.1).
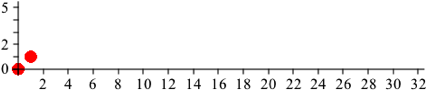
Abb. 1.1: Original und Kopie
Nun verschieben wir eine Kopie der Gesamtfigur (also der beiden Kreise) um 2 Einheiten nach rechts und um eine Einheit nach oben (Abb. 1.2).
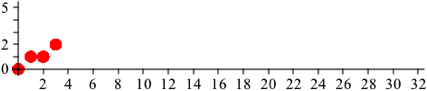
Abb. 1.2: Original und Kopie
Nun verschieben wir eine Kopie der Gesamtfigur (also der vier Kreise) um 4 Einheiten nach rechts und um eine Einheit nach oben (Abb. 1.3).
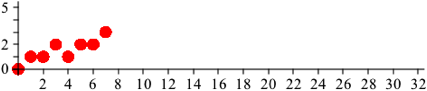
Abb. 1.3: Original und Kopie
Nun verschieben wir eine Kopie der Gesamtfigur (also der acht Kreise) um 8 Einheiten nach rechts und um eine Einheit nach oben (Abb. 1.4).
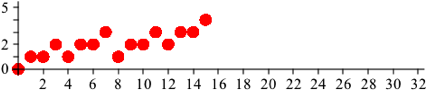
Abb. 1.4: Original und Kopie
Nun verschieben wir eine Kopie der Gesamtfigur (also der 16 Kreise) um 16 Einheiten nach rechts und um eine Einheit nach oben (Abb. 1.5).
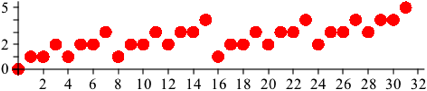
Abb. 1.5: Original und Kopie
Wir sehen, wie der Rekursion lŠuft: In der Abbildung 1.n haben wir 2n Kreise. Wir verschieben eine Kopie davon um 2n Einheiten nach rechts und eine Einheit nach oben.
3 Diskussion
In der Abbildung 2 ist der obere Anschlag eingezeichnet.
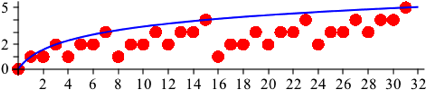
Abb. 2: Oberer Anschlag
Die blaue Kurve hat die Gleichung:
![]() (1)
(1)
Im Wesentlichen also der Logarithmus zur Basis 2. Bei 0, 1, 3, 7, 15, 31, .. haben wir den oberen Anschlag auf den entsprechenden Niveaus 0, 1, 2, 3, 4, 5, .. .
Bei 1, 2, 4, 8, 16, .. haben wir den unteren Anschlag auf dem Niveau 1.
4 SelbstŠhnlichkeit
Wir fŠrben die Kreise im Wechsel rot und blau (Abb. 3.1).
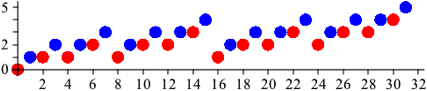
Abb. 3.1: Rot und blau
Und nun lassen wir die blauen Kreise weg (Abb. 3.2).
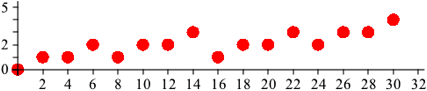
Abb. 3.2: Nur rote Kreise
Die roten Kreise allein bilden im Prinzip dieselbe Figur wie bei der Abbildung 1.4. Die Verschiebungen nach rechts sind doppelt so gro§.
Wenn wir die Gesamtfigur der roten Kreise um eine Einheit nach rechts und eine Einheit nach oben schieben, erhalten wir die Situation der blauen Kreise.
Wir kšnnen also die Figuren der Abbildung 1 in zwei Teilfiguren zerlegen, die im Prinzip dieselbe Struktur haben wie die vorangehende Figur der Abbildung 1. Wir haben so etwas wie eine fraktale Struktur.
5 Niveaus
Die roten Punkte der Abbildung 1.5 haben der Reihe nach die Niveaus (Abb. 4):
0, 1, 1, 2, 1, 2, 2, 3, 1, 2, 2, 3, 2, 3, 3, 4, ..
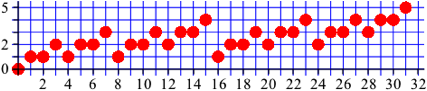
Abb. 4: Niveaus
6 Rekursion
Die Abbildung 5 illustriert die rekursive Struktur dieser Folge.
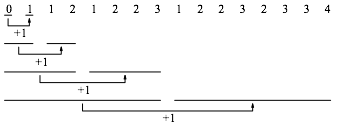
Abb. 5: Rekursive Struktur
Die Folge kann formal rekursiv definiert werden:
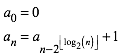 (2)
(2)
Der Beweis ergibt sich aus der Abbildung 5.
7 Quersummen
Die Tabelle 1 zeigt n, unsere Folge an und n binŠr. Wir sehen die Quersummeneigenschaft.
|
n |
an |
n binŠr |
|
n |
an |
n binŠr |
|
0 |
0 |
0 |
|
16 |
1 |
10000 |
|
1 |
1 |
1 |
|
17 |
2 |
10001 |
|
2 |
1 |
10 |
|
18 |
2 |
10010 |
|
3 |
2 |
11 |
|
19 |
3 |
10011 |
|
4 |
1 |
100 |
|
20 |
2 |
10100 |
|
5 |
2 |
101 |
|
21 |
3 |
10101 |
|
6 |
2 |
110 |
|
22 |
3 |
10110 |
|
7 |
3 |
111 |
|
23 |
4 |
10111 |
|
8 |
1 |
1000 |
|
24 |
2 |
11000 |
|
9 |
2 |
1001 |
|
25 |
3 |
11001 |
|
10 |
2 |
1010 |
|
26 |
3 |
11010 |
|
11 |
3 |
1011 |
|
27 |
4 |
11011 |
|
12 |
2 |
1100 |
|
28 |
3 |
11100 |
|
13 |
3 |
1101 |
|
29 |
4 |
11101 |
|
14 |
3 |
1110 |
|
30 |
4 |
11110 |
|
15 |
4 |
1111 |
|
31 |
5 |
11111 |
Tab. 1: Vergleich
8 Verallgemeinerung
Statt mit der Basis 2 arbeiten wir mit der Basis b. Analog zu (2) ergibt sich:
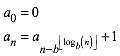 (3)
(3)
Fźr b = 3 erhalten wir die Werte der Tabelle 2.
|
n |
an |
n Basis 3 |
|
n |
an |
n Basis 3 |
|
0 |
0 |
0 |
|
14 |
4 |
112 |
|
1 |
1 |
1 |
|
15 |
3 |
120 |
|
2 |
2 |
2 |
|
16 |
4 |
121 |
|
3 |
1 |
10 |
|
17 |
5 |
122 |
|
4 |
2 |
11 |
|
18 |
2 |
200 |
|
5 |
3 |
12 |
|
19 |
3 |
201 |
|
6 |
2 |
20 |
|
20 |
4 |
202 |
|
7 |
3 |
21 |
|
21 |
3 |
210 |
|
8 |
4 |
22 |
|
22 |
4 |
211 |
|
9 |
1 |
100 |
|
23 |
5 |
212 |
|
10 |
2 |
101 |
|
24 |
4 |
220 |
|
11 |
3 |
102 |
|
25 |
5 |
221 |
|
12 |
2 |
110 |
|
26 |
6 |
222 |
|
13 |
3 |
111 |
|
|
|
|
Tab. 2: Basis 3
Die Abbildung 6 zeigt die zugehšrige Visualisierung. Die blaue Kurve hat die Gleichung:
![]() (4)
(4)
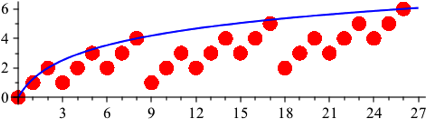
Abb. 6: Basis 3
Fźr b = 4 erhalten wir die Werte der Tabelle 3.
|
n |
an |
n4 |
|
n |
an |
n4 |
|
n |
an |
n4 |
|
n |
an |
n4 |
|
0 |
0 |
0 |
|
16 |
1 |
100 |
|
32 |
2 |
200 |
|
48 |
3 |
300 |
|
1 |
1 |
1 |
|
17 |
2 |
101 |
|
33 |
3 |
201 |
|
49 |
4 |
301 |
|
2 |
2 |
2 |
|
18 |
3 |
102 |
|
34 |
4 |
202 |
|
50 |
5 |
302 |
|
3 |
3 |
3 |
|
19 |
4 |
103 |
|
35 |
5 |
203 |
|
51 |
6 |
303 |
|
4 |
1 |
10 |
|
20 |
2 |
110 |
|
36 |
3 |
210 |
|
52 |
4 |
310 |
|
5 |
2 |
11 |
|
21 |
3 |
111 |
|
37 |
4 |
211 |
|
53 |
5 |
311 |
|
6 |
3 |
12 |
|
22 |
4 |
112 |
|
38 |
5 |
212 |
|
54 |
6 |
312 |
|
7 |
4 |
13 |
|
23 |
5 |
113 |
|
39 |
6 |
213 |
|
55 |
7 |
313 |
|
8 |
2 |
20 |
|
24 |
3 |
120 |
|
40 |
4 |
220 |
|
56 |
5 |
320 |
|
9 |
3 |
21 |
|
25 |
4 |
121 |
|
41 |
5 |
221 |
|
57 |
6 |
321 |
|
10 |
4 |
22 |
|
26 |
5 |
122 |
|
42 |
6 |
222 |
|
58 |
7 |
322 |
|
11 |
5 |
23 |
|
27 |
6 |
123 |
|
43 |
7 |
223 |
|
59 |
8 |
323 |
|
12 |
3 |
30 |
|
28 |
4 |
130 |
|
44 |
5 |
230 |
|
60 |
6 |
330 |
|
13 |
4 |
31 |
|
29 |
5 |
131 |
|
45 |
6 |
231 |
|
61 |
7 |
331 |
|
14 |
5 |
32 |
|
30 |
6 |
132 |
|
46 |
7 |
232 |
|
62 |
8 |
332 |
|
15 |
6 |
33 |
|
31 |
7 |
133 |
|
47 |
8 |
233 |
|
63 |
9 |
333 |
Tab. 3: Basis 4
Die Abbildung 7 zeigt die zugehšrige Visualisierung.

Abb. 7: Basis 4
Die blaue Kurve hat die Gleichung:
![]() (5)
(5)
Websites
The on-line encyclopedia of integer sequences
The on-line encyclopedia of integer sequences
The on-line encyclopedia of integer sequences