Hans Walser, [20131013], [20160331], [20160401]

Quetschwürfel

1 Worum geht es?

Es wird auf die Problematik der in Schulen weitverbreiteten „Schrägbilder“ eingegangen.

2 Das Bild

In Schulbüchern und Arbeitsblättern sieht man oft „Würfel“-Darstellungen wie etwa in der Abbildung 1.

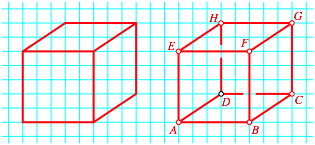
Abb. 1: Was ist denn das?

Ein Würfel kann es allerdings nicht sein. Wenn wir frontal auf eine Würfelseite sehen, ist bei einem massiven Würfel nichts von den anderen Würfelseiten sichtbar. Dies lässt sich leicht an einem Würfelmodell überprüfen.

3 Rekonstruktion und Modell

Wir nehmen nun an, die Abbildung 1 zeige das Orthobild (Orthogonalprojektion, Normalprojektion) eines Spates mit lauter gleich langen Kanten.

Damit können wir den Spat rekonstruieren. Rechnerisch geht das etwa so: Wir wählen ein räumliches kartesisches Koordinatensystem so dass , und . Die Kantenlänge ist also 1. Nun ist zu beachten, dass die y-Achse nicht durch den Punkt D verläuft, sondern orthogonal zum Frontquadrat ABFE hinter A in die Tiefe. Für den Punkt D lesen wir zunächst die zwei Koordinaten und ab. Da die Kante AD die Länge 1 haben soll, folgt , also . Entsprechend lassen sich die Koordinaten der restlichen Punkte berechnen.

Mit Vektorgeometrie lassen sich nun auch die Winkel und bestimmen.

Die Abbildung 2 zeigt eine Abwicklung des Spates.

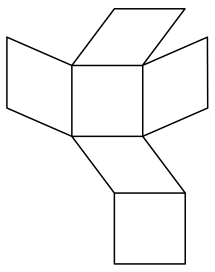
Abb. 2: Abwicklung des Quetschwürfels

Ein aus diese Abwicklung gebautes Papier- oder Kartonmodell kann nun entsprechend der Abbildung 1 gesehen werden (Abb. 3a). Ein Würfel ist es aber nicht (Abb. 3b). Es ist im wörtlichen Sinn eine falsche Schachtel.

Abb. 3: Quetschwürfel

4 Vergleich mit Normalprojektion

Die Abbildung 4 zeigt den Vergleich mit der Normalprojektion eines echten Würfels. Die angedeuteten Seitenflächen sind in den beiden Darstellungen kongruent.

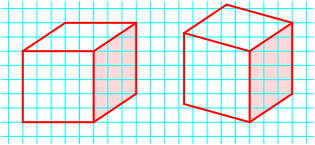
Abb. 4: Quetschwürfel und Würfel

5 Fehlende Eindeutigkeit

Die Abbildung 5 zeigt eine Serie von Schrägbildern. Welches ist der Würfel?

Abb. 5: Welches ist der Würfel?

Die Frage kann nicht entschieden werden. Nach den Regeln des Schrägbildes muss die Tiefendimension (Richtung nach „hinten“) zusätzlich mit einer Einheit versehen werden. Anders gesagt: Es muss zusätzlich gesagt werden, welches der Würfel ist (Eichwürfel).

Die Abbildung 6 zeigt dieselbe Würfelserie in Normalprojektion. Die farbige rechte Seitenfläche ist jeweils übernommen worden.

Abb. 6: Alles Würfel

6 Argumente für das Schrägbild

6.1 Schattenbild

Das Schattenbild eines Kantenwürfels ist (wegen der großen Entfernung der Sonne von der Erde) annähernd ein Schrägbild. Dieses ist also „natürlich“.

6.2 Einfachheit

In Auseinandersetzung mit Lehrpersonen und Schulbuchautoren wird immer wieder die „Einfachheit“ des Schrägbildes hervorgehoben. Schülerinnen und Schüler können auf Karopapier selber und rasch zeichnen.

7 Argumente gegen das Schrägbild

Die „Einfachheit“ ist richtig, solange wir uns auf Polyeder beschränken. Sobald krumme Flächen (Zylinder, Kegel, Kugel) ins Spiel kommen wird die Sache problematisch. Die korrekten Schrägbildfiguren sehen unnatürlich aus.

Die folgenden beiden Abbildungen basieren auf dem Schrägbild der Abbildung 1.

Die Abbildung 7 zeigt einen dem „Würfel“ einbeschriebenen geraden Kreiszylinder.

Abb. 7: Quetschzylinder

Zum Vergleich dazu die Darstellung desselben Zylinders in Normalprojektion (Abb. 8).

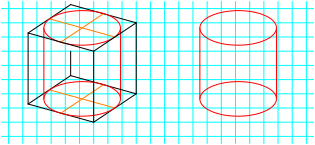
Abb. 8: Zylinder

Die menschliche Wahrnehmung ist sehr sensibel auf „falsche“ Kreisbilder. Die Ellipse mit horizontaler Symmetrieachse (Abb. 8) wird als „richtiges“ Kreisbild empfunden, die schiefe Ellipse (Abb. 7) als „falsch“. Das führt dann gelegentlich dazu, dass „korrigiert“ wird wie etwa in Abbildung 9.

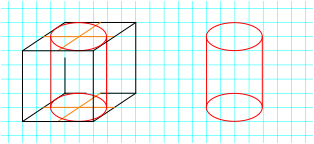
Abb. 9: „Korrigierter“ Quetschzylinder

Im Kontext des Würfels ist der Fehler sofort einsichtig. Der Deckkreis müsste die Mittelpunkte der oberen Würfelkanten berühren, was er aber offensichtlich nicht tut. Bei der Darstellung des freistehenden Zylinders können wir kaum glauben, dass der Zylinder gleich dick wie hoch sein soll.

Bei der Abbildung 8 ist dagegen alles in Ordnung.

Die Abbildung 10 zeigt einen dem „Würfel“ einbeschriebenen geraden Kreiskegel.

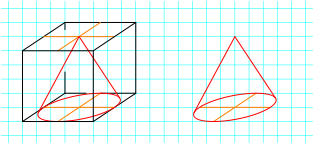
Abb. 10: Quetschkegel

Die Figuren sehen echt bescheuert aus (Kommentar eines Kollegen). Zum Vergleich dazu die Normalprojektion desselben Kegels (Abb. 11).

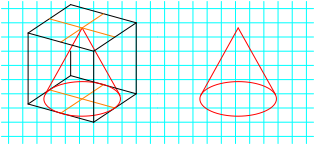
Abb. 11: Kegel

Der Umriss einer Kugel erscheint im Schrägbild als Ellipse (Abb. 12). Das sieht man am Schattenbild. In der Normalprojektion ergibt sich ein Kreis als Kugelumriss.

Abb. 12: Schatten als Quetschkugel

Der Umriss der Inkugel eines Würfels im Schrägbild ist eine Ellipse (Abb. 13). Der Äquator ist schief.

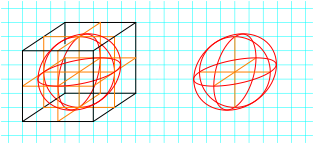
Abb. 13: Quetschkugel

Diese Ellipse oft auf einen Kreis „korrigiert“. Dies ist einer der häufigsten Darstellungsfehlern in Schulbüchern und Unterrichtsmaterialien.

Zum Vergleich zur Quetschkugel die Normalprojektion derselben Kugel (Abb. 14). Der Äquator ist horizontal.

Abb. 14: Kugel

Korrekte Kreis- und Kugelzeichnungen im Schrägbild sind (für uns heutige) nicht einfach herzustellen. Am besten ist es, dazu eine 3d-Grafik-Software zu verwenden.

8 Didaktisches

Wer macht es besser? Wir brauchen nicht lange zu suchen. Die Bauanleitungen von LEGO® verwenden ein Darstellungsprinzip (Normalprojektion oder Normalaxonometrie), das zum Würfelbild der Abbildung 15 führt. Damit werden schon Kinder im Vorschulalter mit guten Raumdarstellungen vertraut.

Abb. 15: Der schöne Würfel

Und viele Software lädt zum Zeichnen von dreidimensionalen Figuren ein. Meist steht dabei sogar eine Perspektive zur Verfügung.

9 Normalaxonometrie im Quadratraster

Als Argument für den Schrägbild-„Würfel“ wird oft die leichte Zeichenbarkeit im Karoraster verwendet. Tatsächlich können aber auch exakte normalaxonometrische Würfelbild im Quadratraster gezeichnet werden. Die Abbildungen 16 und 17 geben je ein Beispiel.

Abb. 16: Normalaxonometrie im Raster

Abb. 17: Normalaxonometrie im Raster

Beide Lösungen haben den Nachteil, dass es vergleichsweise große Würfel gibt. Immerhin sind die Lösungen in einem 4mm Quadratraster auf DIN A4 Papier machbar.

Es gibt unendlich viele exakte Rasterlösungen [Vgl. [20131014] ].

10 Approximationen

Normalaxonometrische Würfelbilder lassen sich natürlich auch approximativ in den Karoraster einpassen. Das gibt dann weniger große Bilder. Die Abbildung 18a) zeigt ein normalaxonometrisches Würfelbild (die oberen vier Ecken passen nicht in den Raster), während die Abbildung 18b) eine in den Raster passende Approximation darstellt. Die Approximation ist um etwa 3.9% zu hoch.

Abb. 18: Normalaxonometrie und Approximation

Die Abbildung 19 zeigt eine Variante. Die Approximation im Raster (Abb. 19b) ist 1.8% zu niedrig.

Abb. 19: Variante

11 Normalaxonometrie mit dynamischer Geometrie Software

Im Folgenden eine rezeptmäßige Darstellung eines an sich exakten Vorgehens.

Wir haben gesehen, dass unser „Gefühl“ für eine korrekte Darstellung eng an die Darstellung eines Kreises als Ellipse verknüpft ist.

11.1 Rezept

Wir orientieren uns an der Abbildung 8 und beginnen daher gleich mit der Ellipse.

Wir wählen die beiden Brennpunkte F und G auf einer horizontalen Geraden. Dazu die Mittelsenkrechte und darauf einen Punkt P (Abb. 20).

Abb. 20: Start

Nun zeichnen wir die Ellipse mit diesen beiden Brennpunkten durch P (Abb. 21). In dynamischer Geometrie Software steht ein Button dazu zur Verfügung.

Abb. 21_ Ellipse

Auf der Ellipse wählen wir einen Punkt Q und zeichnen den dazu diametralen Punkt (Abb. 22).

Abb. 22: Punkt auf Ellipse und diametraler Punkt

In diesen beiden Punkten zeichnen wir die Tangente an die Ellipse (Abb. 23).

Abb. 23: Tangenten

Wir zeichnen die Mittelparallele zu den beiden Tangenten und schneiden sie mit der Ellipse. In den Schnittpunkten zeichnen wir erneut Tangenten an die Ellipse (Abb. 24).

Abb. 24: Mittelparallele und weitere Tangenten

Die vier Tangenten bilden ein Viereck. Dieses ist das Bild des Deckquadrates unseres Würfels.

Die zum Deckquadrat senkrechten Würfelkanten sind parallel zur kurzen Ellipsenachse zu zeichnen (Abb. 25).

Abb. 25: Weitere Würfelkanten

Die Länge der Bilder dieser Würfelkanten ist gleich dem Abstand der beiden Brennpunkte F und G (Abb. 26). Dies ist der Gag dieser Konstruktion.

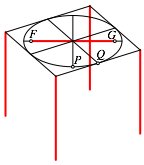
Abb. 26: Abstand der Brennpunkte

Nun können wir zum Würfelbild ergänzen und das Bild grafisch aufpeppen (Abb. 27).

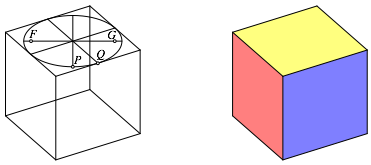
Abb. 27: Bild des Würfels

11.2 Kommentare

Das Verfahren ist rein planimetrisch und hat nichts mit 3d Geometrie Software zu tun. Das wäre ein anderes Thema und sicher viel einfacher.

Die lange Achse der Ellipse ist die wirkliche Kantenlänge des Würfels.

Die Geometrie der Kegelschnitte war zu Zeiten von Zirkel und Lineal eine aufwändige Sache. Mit dynamischer Geometrie Software geht alles viel einfacher.

Mit den vier Punkten F, G, P, Q können wir das Bild verändern.

Mit dem Punkt Q können wir den Würfel um die senkrechte Achse drehen (Ab. 28). Die Ellipse bleibt unverändert.

Abb. 28: Drehen des Würfels

Durch auf- und Abschieben des Punktes P wird der Würfel um eine horizontale Achse gekippt (Abb. 29).

Abb. 29: Kippen des Würfels

Bis jetzt haben wir immer nur „stehende“ Würfel gezeichnet, die auf einer horizontalen Unterlage stehen.

Durch Verändern der Brennpunkte, so dass sie nicht mehr auf einer horizontalen Geraden liegen, erreichen wir Bilder von Würfeln, welche schief in den Raum eingebettet sind (Abb. 30).

Abb. 30: Schiefe Bettung