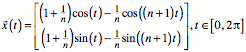Hans Walser, [20100215a]
Radlinien
1 Worum es geht
Wir rollen auf dem
Einheitskreis einen anderen Kreis ab und verfolgen die Bahn eines Punktes auf
der Peripherie des abrollenden Kreises.
Es werden Kurvenlnge
und Flcheninhalt der Radlinien berechnet.
2
Radlinie au§en
2.1
Parameterdarstellung
Der abrollende Kreis habe
den Radius ![]() und rolle au§en
auf dem Einheitskreis ab. Diese Radlinie kann beschrieben werden durch:
und rolle au§en
auf dem Einheitskreis ab. Diese Radlinie kann beschrieben werden durch:
Der Mittelpunkt des abrollenden
Kreises dreht auf einem Kreis mit Radius ![]() im positiven
Drehsinn, der abrollende Kreis mit Radius
im positiven
Drehsinn, der abrollende Kreis mit Radius ![]() dreht sich ebenfalls
im positiven Drehsinn, und zwar
dreht sich ebenfalls
im positiven Drehsinn, und zwar ![]() Mal pro Umlauf. Das
kennen wir aus der Astronomie: Die Erde dreht sich bei einem Umlauf um die
Sonne gegenber den Fixsternen ein Mal mehr als gegenber der Sonne. Daher sind
die Sternentage krzer als die Sonnentage.
Mal pro Umlauf. Das
kennen wir aus der Astronomie: Die Erde dreht sich bei einem Umlauf um die
Sonne gegenber den Fixsternen ein Mal mehr als gegenber der Sonne. Daher sind
die Sternentage krzer als die Sonnentage.
Die Abbildung zeigt die
Radlinie fr ![]() .
.
Radlinie au§en fr n = 5
Die Radlinie hat n einwrts gerichtete Spitzen.
2.2
Lngenberechnung
Aus der
Parameterdarstellung erhalten wir mit einiger Rechnung:

Fr die Kurvenlnge ![]() rechnen wir n Mal die Lnge eines Bogens:
rechnen wir n Mal die Lnge eines Bogens:
Bemerkenswert ist, dass
diese Kurvenlnge rational ist, obwohl die Kurve auf Kreisen und
Kreisbewegungen basiert. Dieses Beispiel hatte frher die Hoffnung genhrt,
dass die Kreiszahl ¹ vielleicht rational sein knnte. Erst Johann Heinreich
Lambert (1728-1777) konnte 1768 beweisen, dass die Kreiszahl ¹ irrational ist.
2.2.1
Ein Irrtum
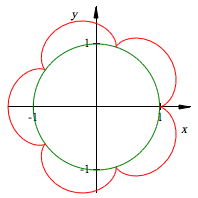
Offensichtlich ist ![]() . Andererseits nhert sich die Radlinie fr
. Andererseits nhert sich die Radlinie fr ![]() dem
Einheitskreis. Die Abbildung zeigt die Radlinie fr
dem
Einheitskreis. Die Abbildung zeigt die Radlinie fr ![]() .
.
Radlinie mit 100 Spitzen
Daraus knnte der
falsche Schluss gezogen werden, der Einheitskreis habe den Umfang 8. Warum ist
dieser Schluss falsch?
2.3
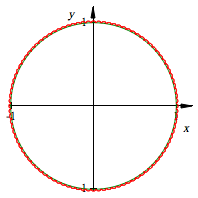
Flchenbrechung
Wie gro§ ist der
Flcheninhalt?
Aus
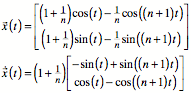
ergibt sich:
![]()
Wegen
![]()
erhalten wir:
![]()
Der Flcheninhalt ist
ein rationales Vielfaches von ¹. Es ist:
![]()
Warum ist der Schluss,
der Einheitskreis habe den Flcheninhalt ¹, nun richtig?
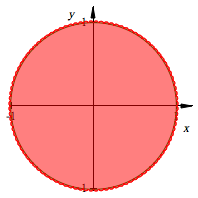
Fast der Einheitskreis
3
Radlinie innen
Der abrollende Kreis
habe wieder den Radius ![]() und rolle nun
innen auf dem Einheitskreis ab. Diese Radlinie kann beschrieben werden durch:
und rolle nun
innen auf dem Einheitskreis ab. Diese Radlinie kann beschrieben werden durch:
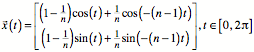
Der Mittelpunkt des
abrollenden Kreises dreht auf einem Kreis mit Radius ![]() im positiven
Drehsinn, der abrollende Kreis mit Radius
im positiven
Drehsinn, der abrollende Kreis mit Radius ![]() dreht sich nun
im negativen Drehsinn, und zwar
dreht sich nun
im negativen Drehsinn, und zwar ![]() Mal pro Umlauf.
Die Abbildung zeigt die Radlinie fr
Mal pro Umlauf.
Die Abbildung zeigt die Radlinie fr ![]() . Die Spitzen sind nun nach au§en gerichtet.
. Die Spitzen sind nun nach au§en gerichtet.
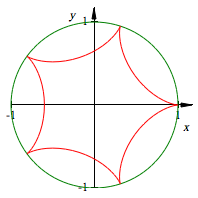
Radlinie innen fr n = 5
Mit analogen Rechnungen
finden wir fr die Kurvenlnge ![]() und den
Flcheninhalt
und den
Flcheninhalt ![]() :
:
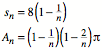
4
Rationaler Kreisradius
Wir ersetzen n durch den gekrzten Bruch ![]() . Nun mssen wir mit q Umlufen arbeiten, bis sich die Kurve schlie§t.
. Nun mssen wir mit q Umlufen arbeiten, bis sich die Kurve schlie§t.
4.1
Abrollen au§en
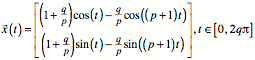
Die Abbildung zeigt die
Radlinie fr ![]()
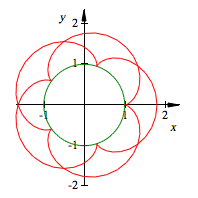
Blumenmuster
Fr Kurvenlnge ![]() und
Flcheninhalt
und
Flcheninhalt ![]() gilt:
gilt:
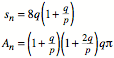
Bei der Flchenformel
ist zu beachten, dass wir bis zu q-fache
berlappungen haben. Meine Software frbt parittisch nach Anzahl der
berlappungen. Bei einer geraden Anzahl von berlappungen wird nicht gefrbt.
Fr ![]() sieht das so
aus:
sieht das so
aus:
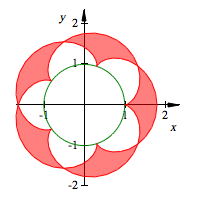
Frbung
Fr ![]() sieht das so
aus:
sieht das so
aus:

Frbung
Fr ![]() sieht das so
aus:
sieht das so
aus:

Frbung
4.1.1
Sonderfall: p = 1
Wenn wir ![]() setzen, hei§t
das, dass wir auf dem Einheitskreis au§en einen Kreis vom Radius q abrollen.
setzen, hei§t
das, dass wir auf dem Einheitskreis au§en einen Kreis vom Radius q abrollen.
Die Abbildung zeigt den
Fall fr ![]() .
.
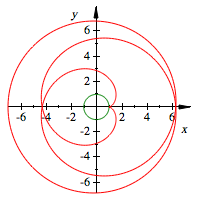

Kreis mit Radius 3 wird
abgerollt
4.2
Abrollen innen
Wenn wir innen
abrollen, ergeben sich wieder Spitzen.
4.2.1
Radius < 1
Damit der Kreis
wirklich im Innern abrollen kann, muss sein Radius kleiner als 1 sein. Daher
muss ![]() gelten.
gelten.
Die Abbildung zeigt den
Fall ![]() .
.
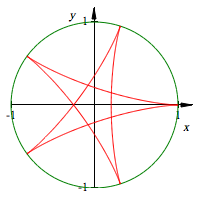

Sternfigur
4.2.2
Radius > 1
Wenn der Radius des
ãabrollendenÒ Kreises aber gr§er als eins ist, haben wir ein ãAbwlzenÒ und
die Kurve verluft im u§eren des Einheitskreises. Fr ![]() etwa erhalten
wir:
etwa erhalten
wir:
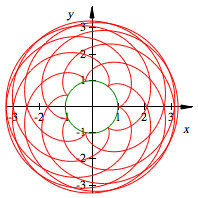

Abwlzen
Das entspricht der
Figur, die beim u§eren Abrollen mit ![]() entsteht. Der
Hintergrund ist folgender: Unsere Figuren entstehen durch berlagerung zweier
Kreisbewegungen. Formelm§ig geschieht das durch eine Addition. Wegen der
Kommutativitt der Addition ist es aber willkrlich, welchen Kreis wir als
ãerstenÒ und welchen als ãzweitenÒ Kreis whlen.
entsteht. Der
Hintergrund ist folgender: Unsere Figuren entstehen durch berlagerung zweier
Kreisbewegungen. Formelm§ig geschieht das durch eine Addition. Wegen der
Kommutativitt der Addition ist es aber willkrlich, welchen Kreis wir als
ãerstenÒ und welchen als ãzweitenÒ Kreis whlen.