Hans Walser, [20221120]

Rasterellipsen und Goldener Schnitt

1 Worum geht es?

Ellipsen in einem Quadratraster führen zu Figuren, die Strecken im Längenverhältnis des Goldenen Schnittes enthalten.

2 Konstruktionsvorgang

Wir arbeiten in einem quadratischen 3×3-Raster (Abb. 1).

Abb. 1: Raster

In diesem Raster legen wir zwei Brennpunkte einer Ellipse fest (Abb. 2). Die Ellipse soll durch einen weiteren Rasterpunkt verlaufen.

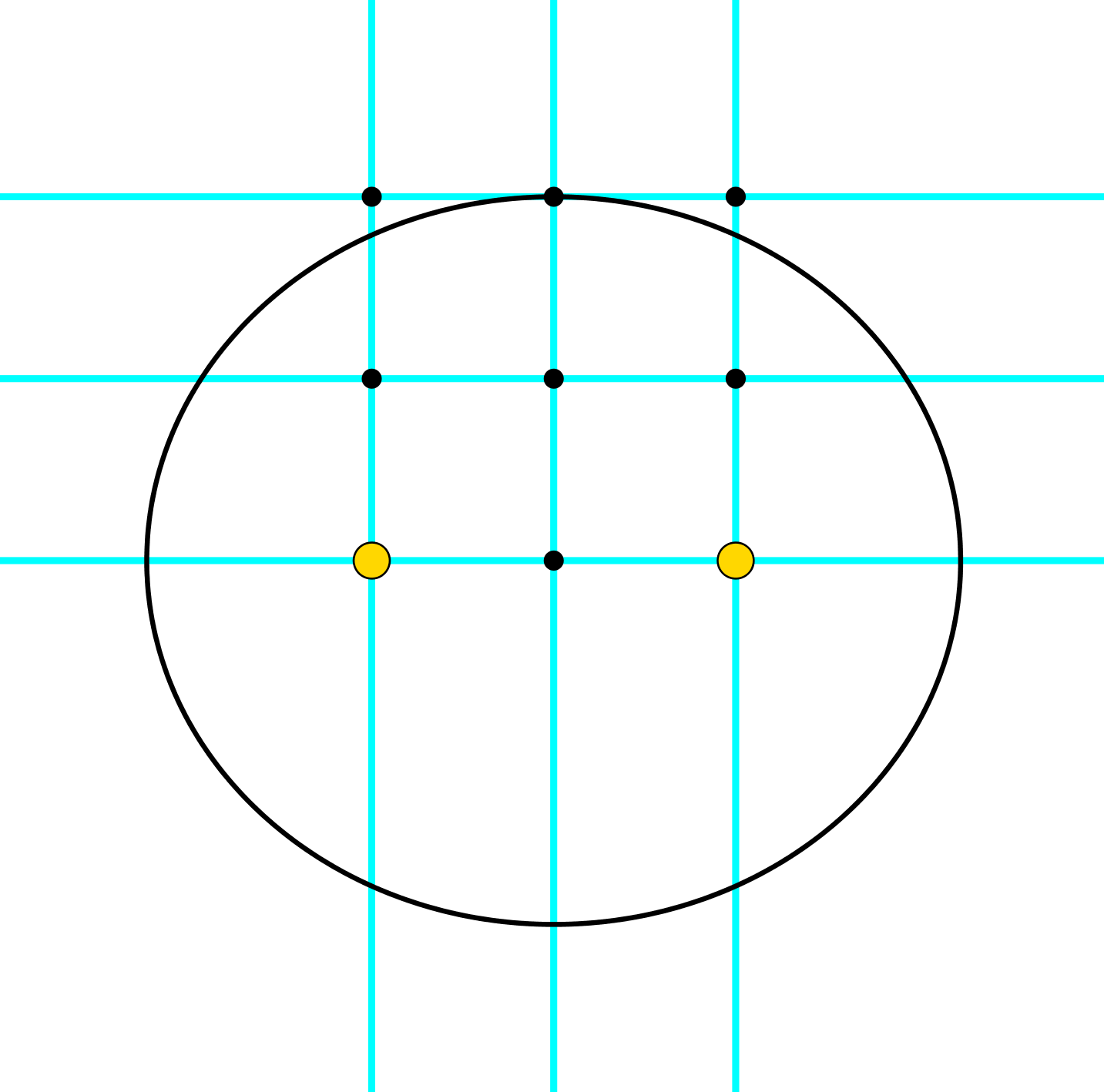
Abb. 2: Brennpunkte und Ellipsenpunkt

In der Figur suchen wir zwei Strecken, deren Längen im Verhältnis des Goldenen Schnittes stehen. Die längere Strecke („Major“) wird rot, die kürzere („Minor“) blau gezeichnet. Die Abbildung 3 zeigt ein Beispiel.

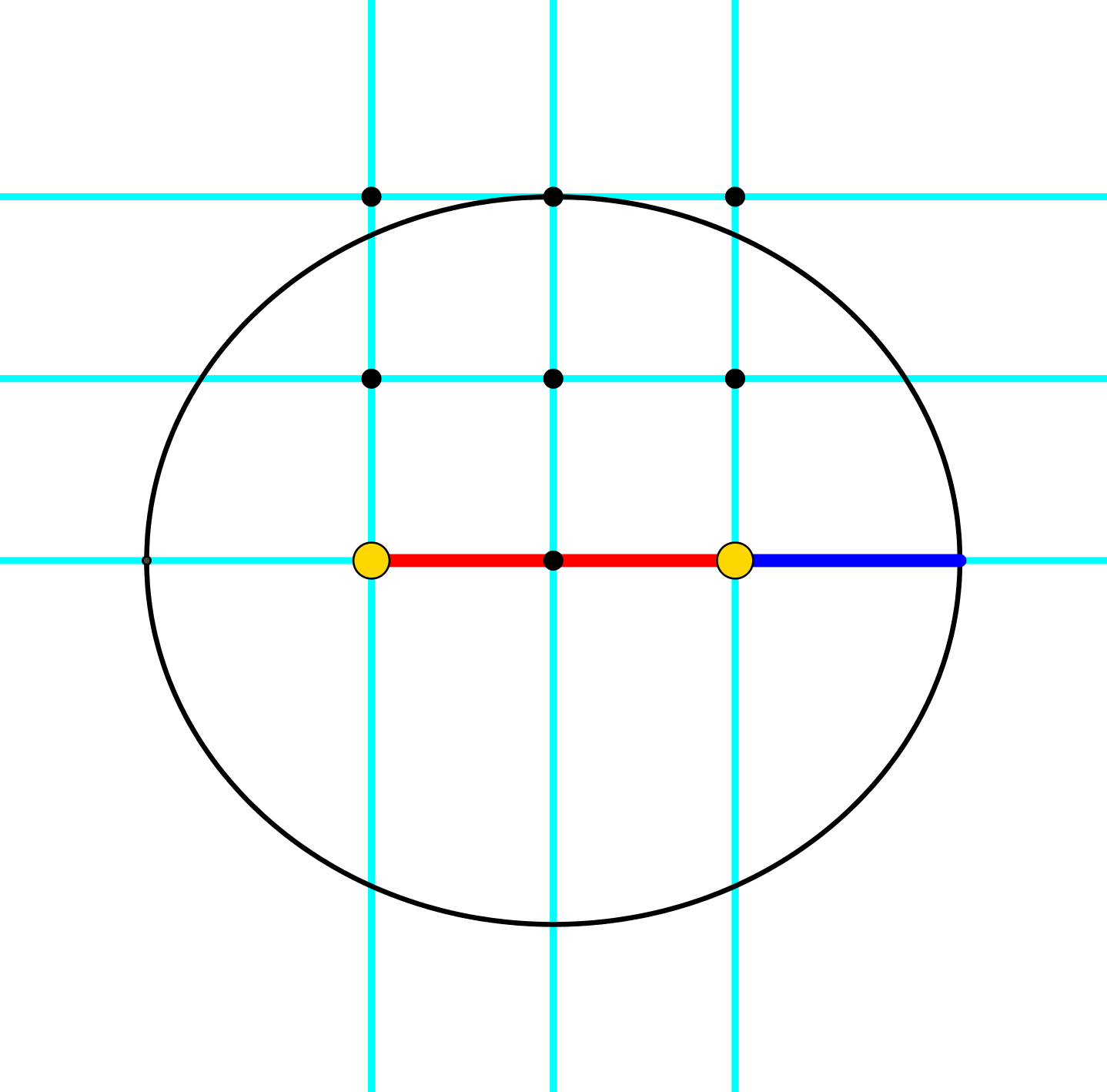
Abb. 3: Goldener Schnitt

Zur selben Ellipse kann es mehrere Lösungen geben (Abb. 4).

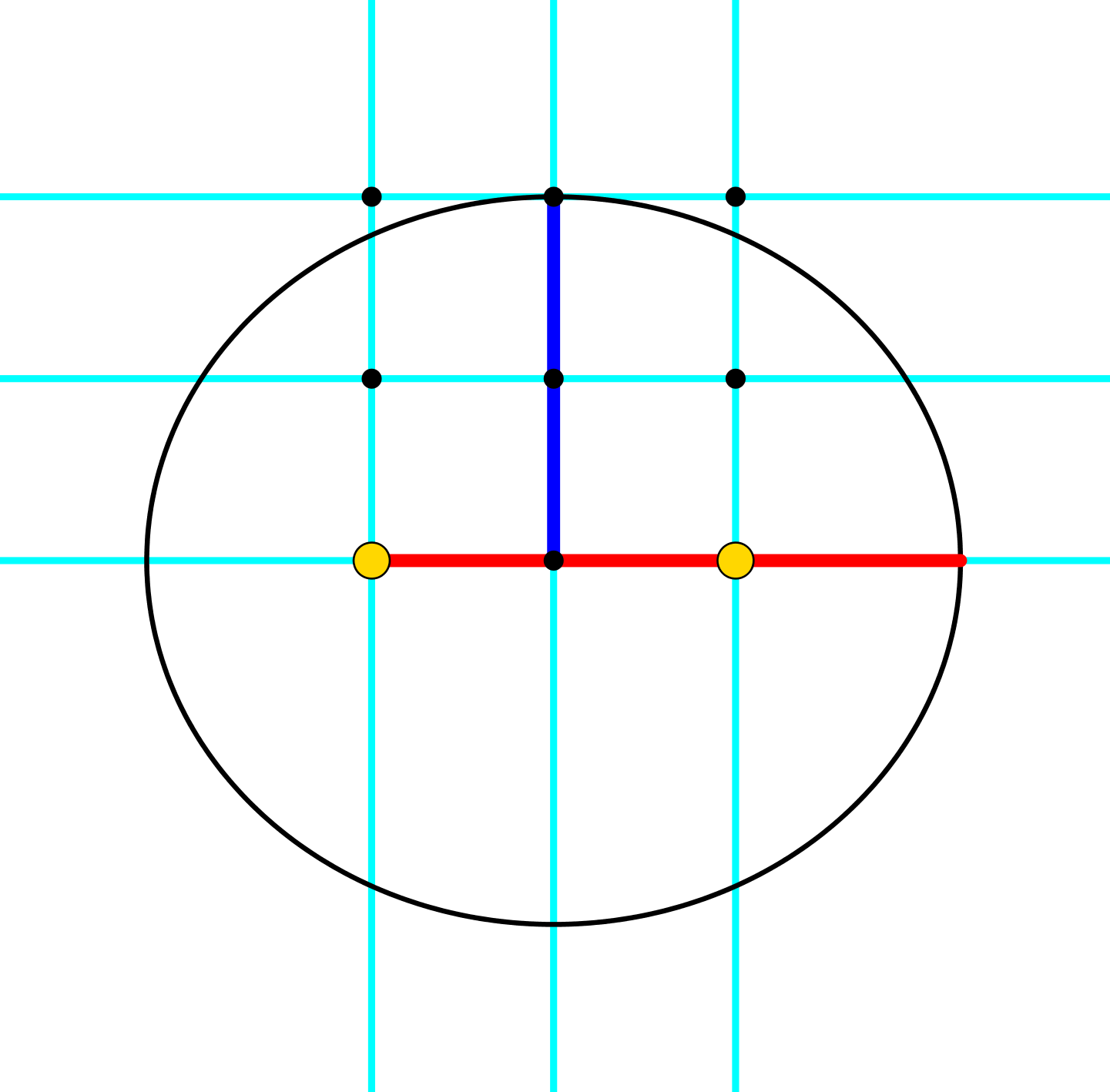
Abb. 4: Eine weitere Lösung

3 Beispiele

Im Folgenden einige Beispiele ohne systematische Ordnung.

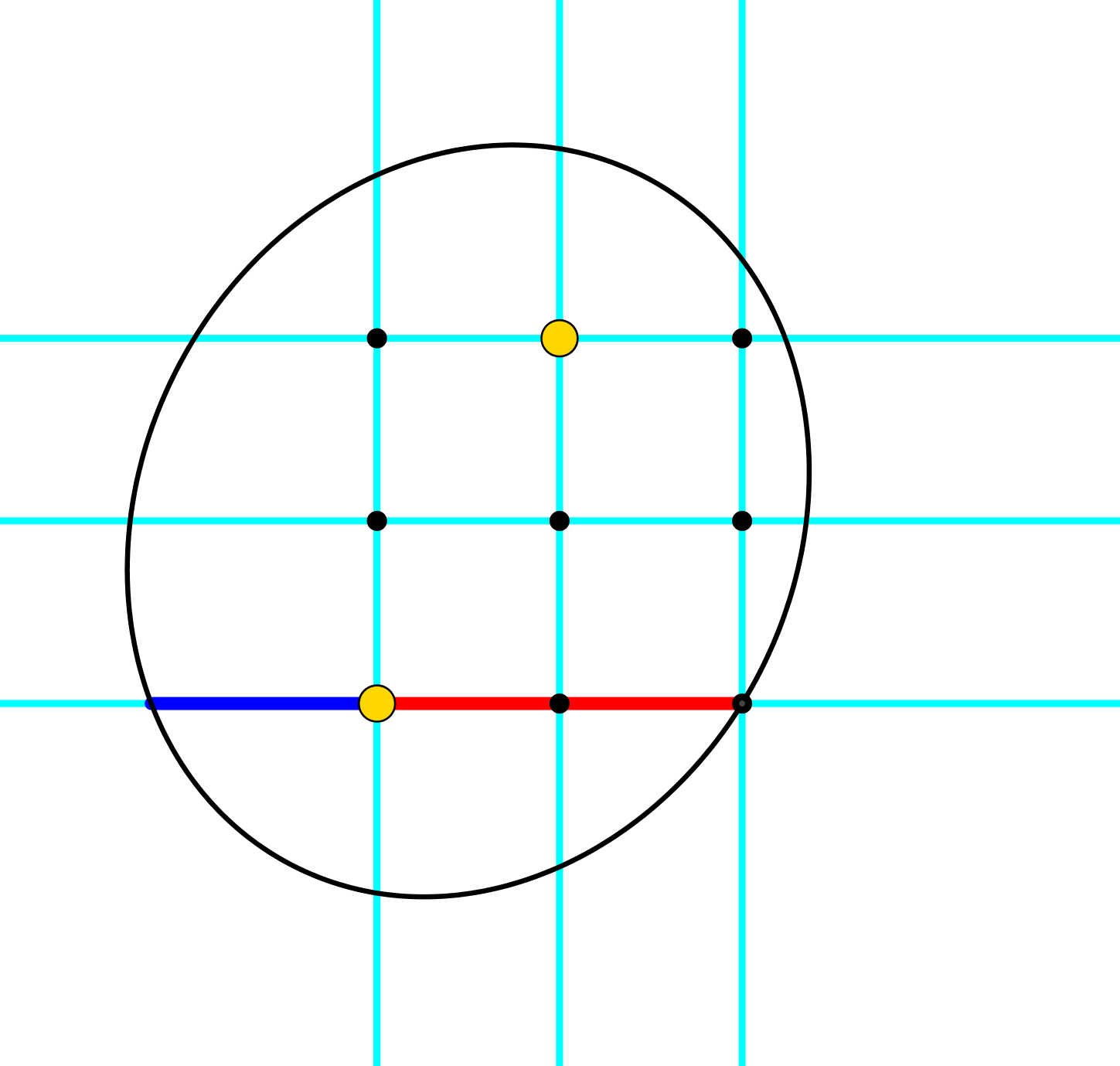
Abb. 5

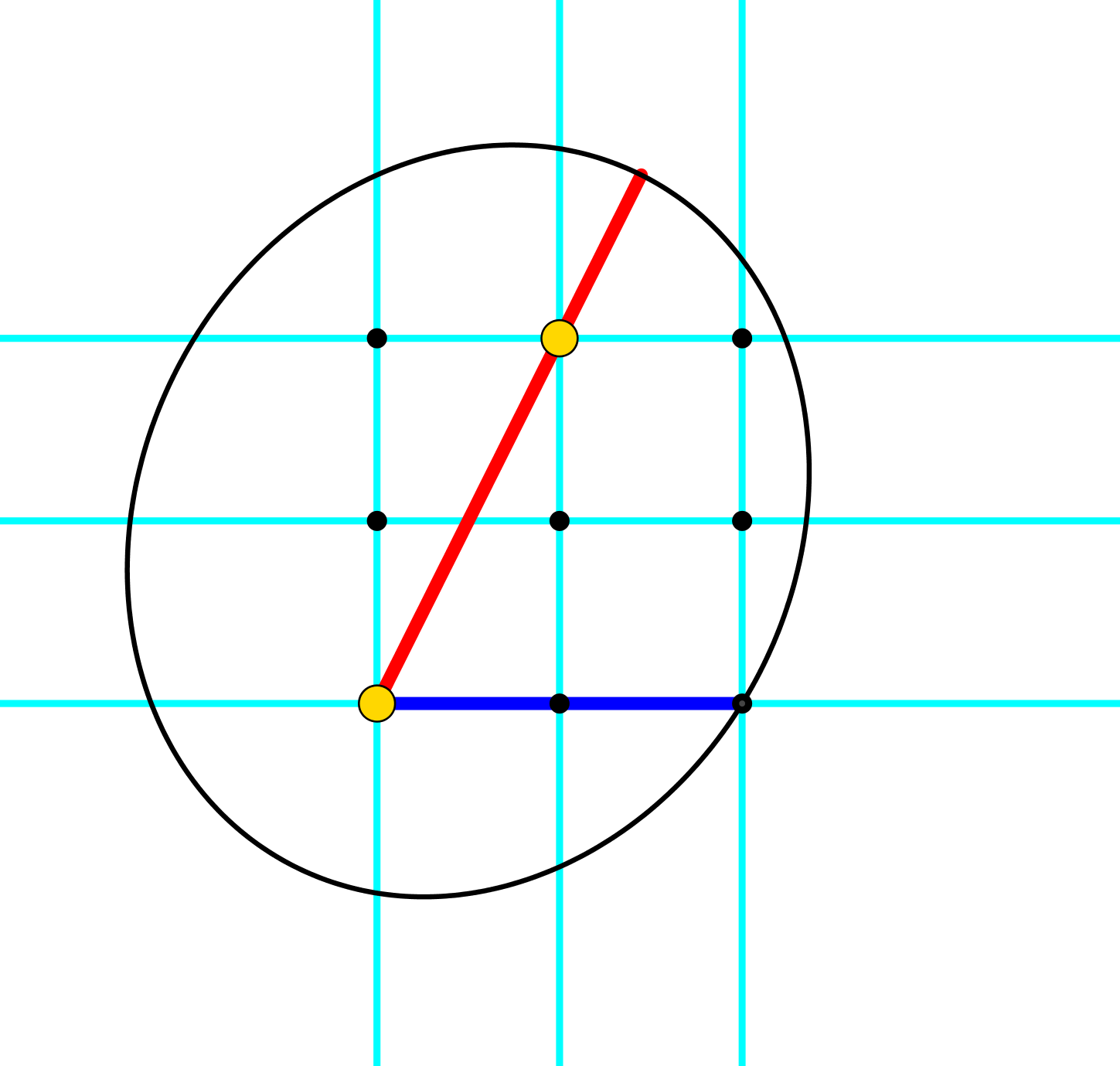
Abb. 6

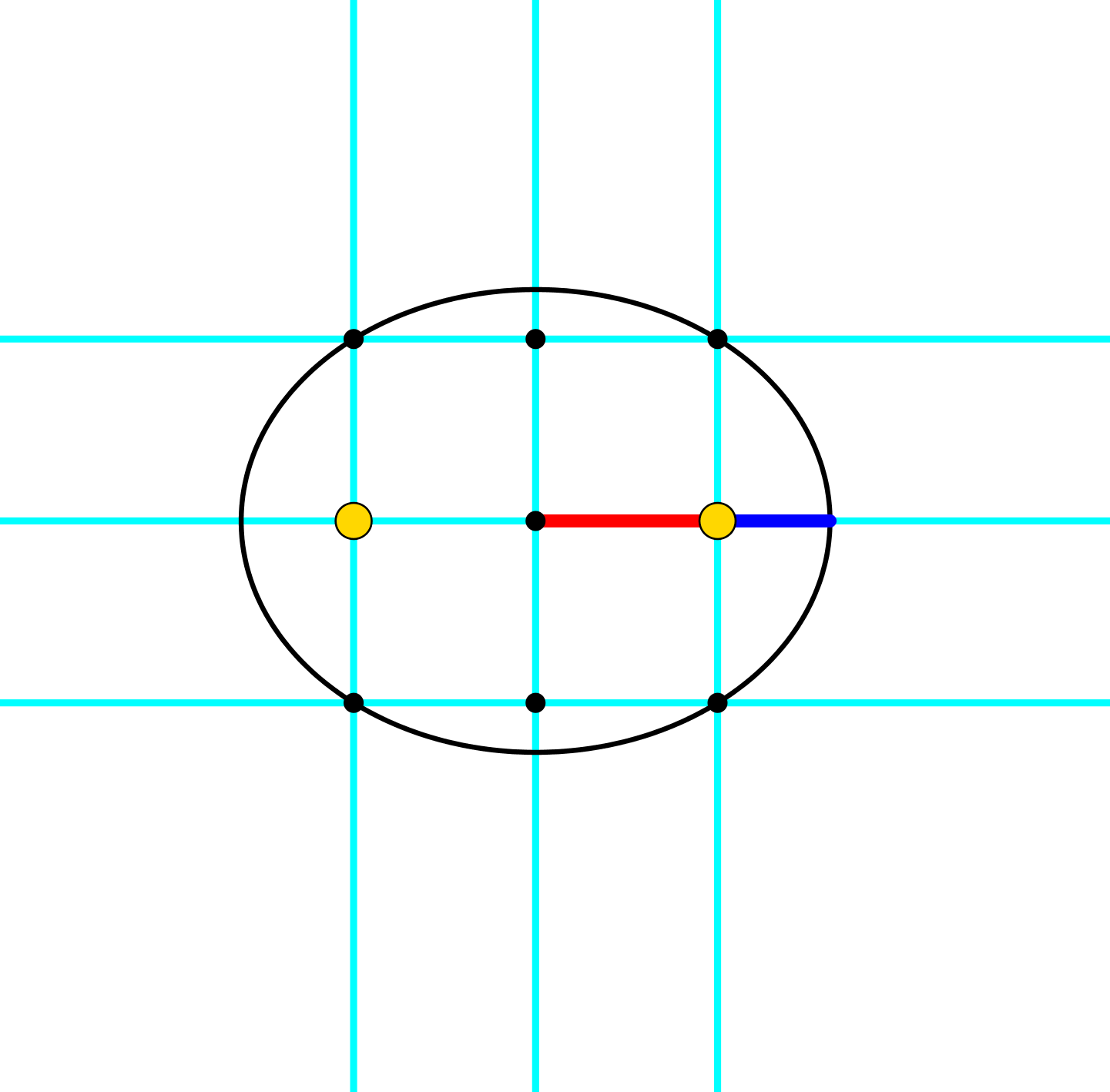
Abb. 7

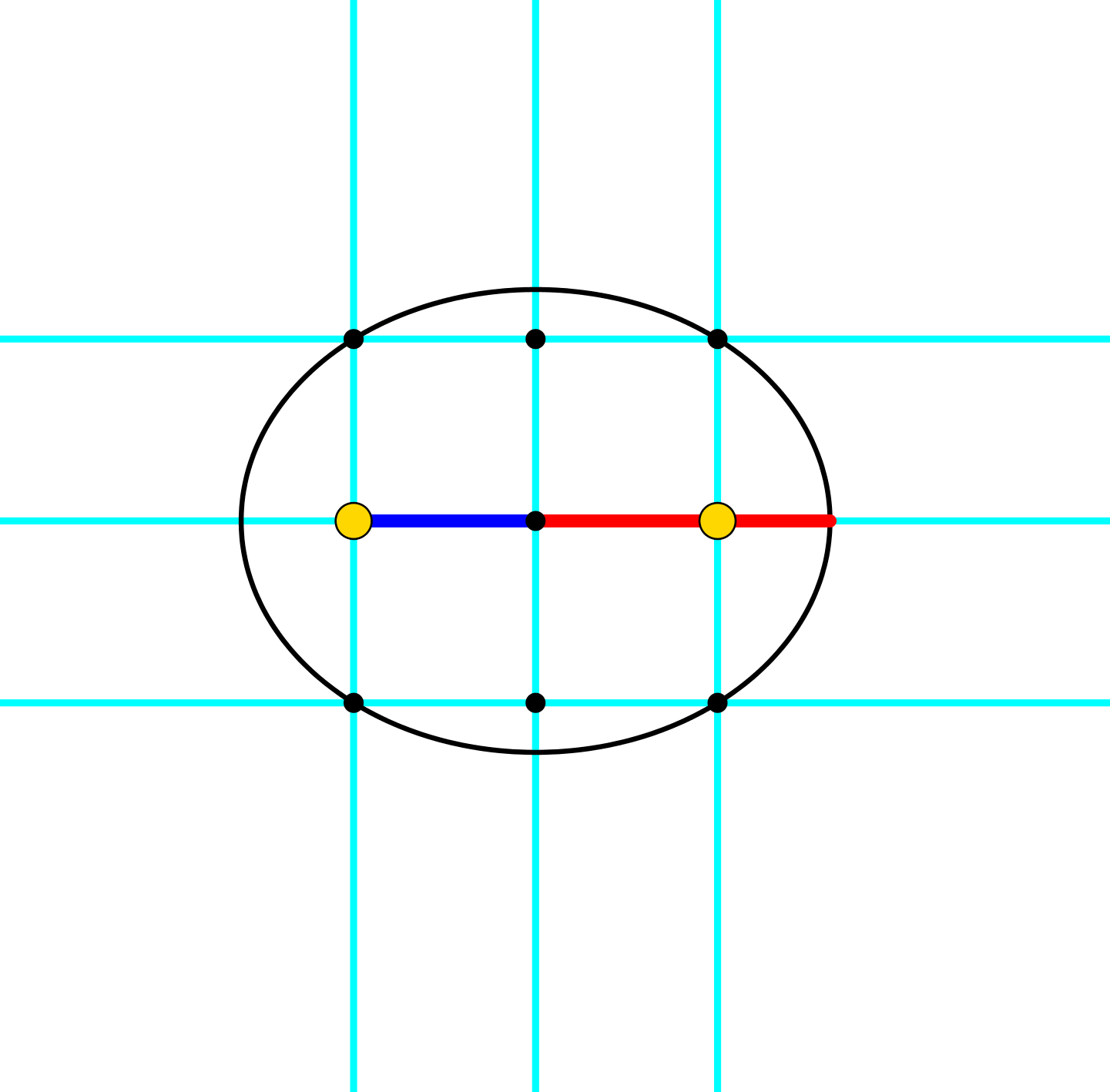
Abb. 8

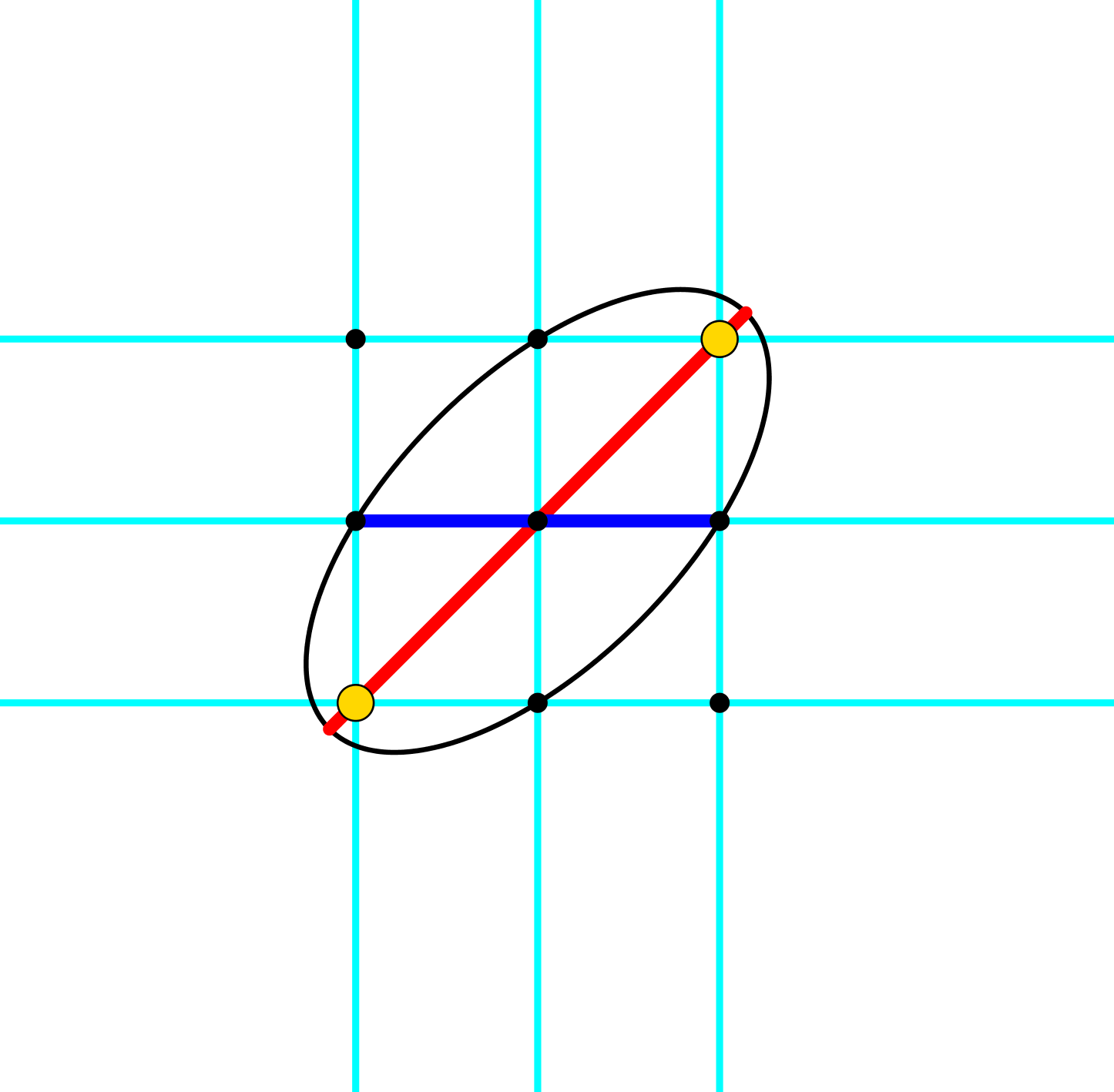
Abb. 9

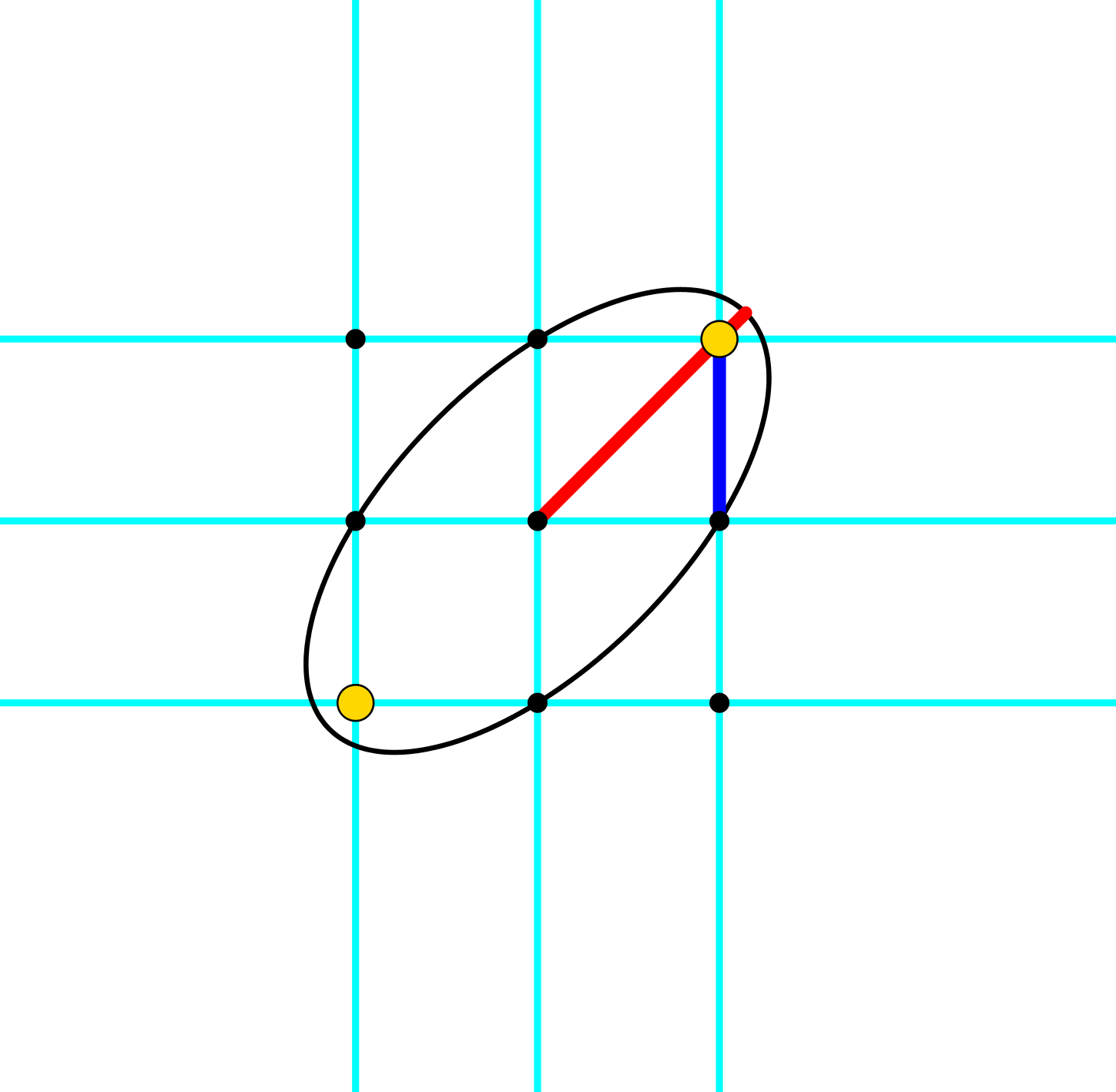
Abb. 10

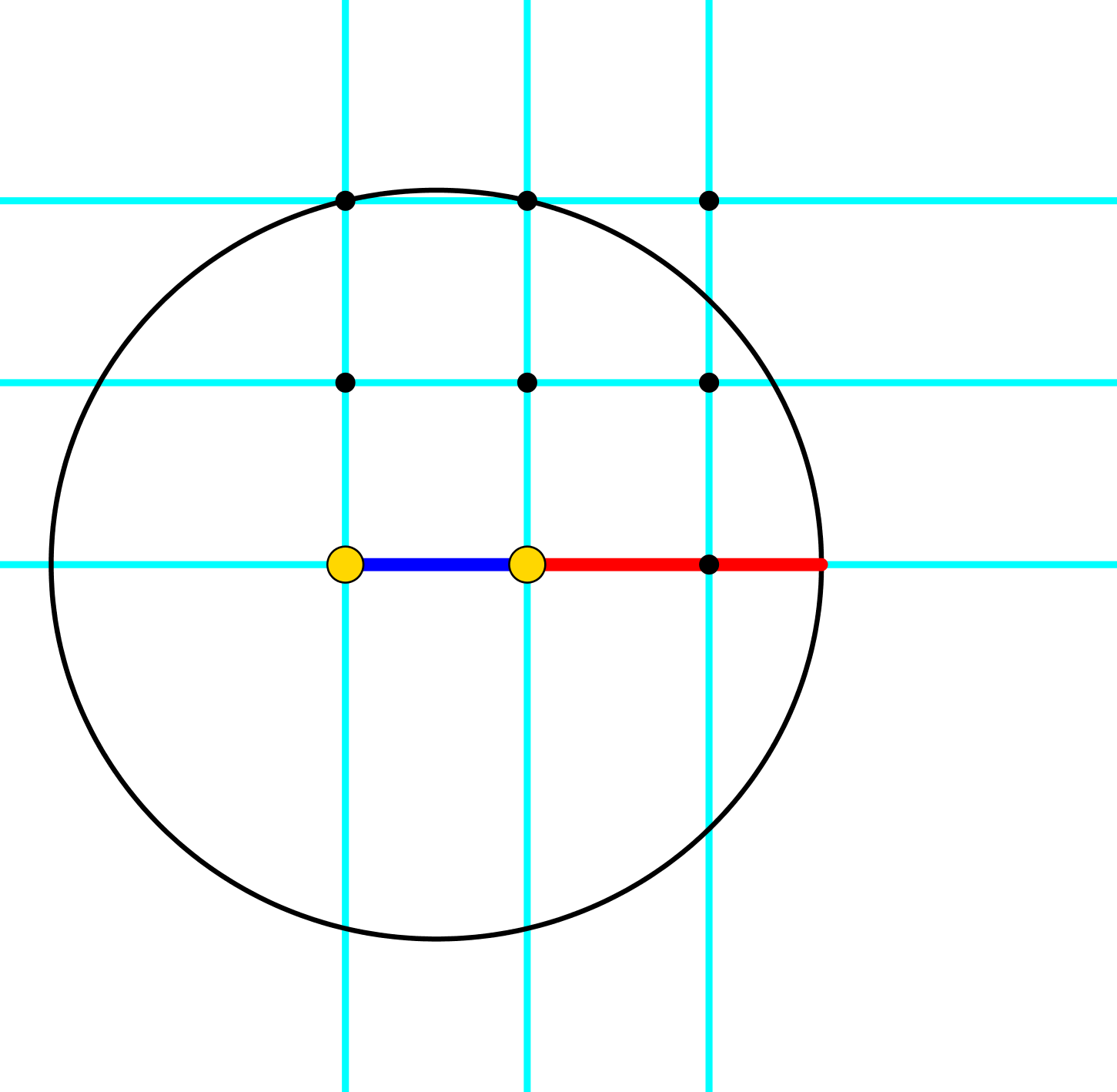
Abb. 11

Abb. 12

4 Ausblick

Größerer Raster

Hyperbeln

Parabeln

Dreiecksraster

Literatur

Walser, Hans (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Edition am Gutenbergplatz, Leipzig. ISBN 978-3-937219-85-1.